Определение грузоподъемности статически. определимой конструкции, работающей на растяжение-сжатие (задача № 3)

определимой конструкции, работающей на растяжение-сжатие (задача № 3)

Условие задачи

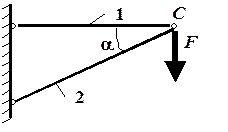Рис. 1.5. Схема конструкции в задаче № 3

Конструкция, состоящая из стержней, соединенных шарнирами, загружена силой F (рис. 1.5). Сечения стержней – из стальных прокатных профилей. Площади сечений нужно взять из сортамента (смотри, например, в [1]). Цель расчета:

1) определить значение допускаемой нагрузки;

2) найти перемещение узла С.

Примечание. Если на схеме, выбранной студентом по [4], один стержень показан более жирным, то его следует считать абсолютно жестким, т. е. деформациями этого стержня следует пренебречь.

Решение

    Рис. 1.6. План сил

Для определения усилий используем метод сечений. Для этого нарисуем план сил: рассечем деформируемые стержни конструкции и отброшенные части стержней заменим продольными силами N ₁ и N ₂ (рис. 1.6). Найдем усилия N ₁ и N ₂ из уравнений равновесия отсеченной части конструкции. Желательно составлять такие уравнения равновесия, чтобы в каждое уравнение входило только одно неизвестное усилие, например, для определения N ₁ и (рис. 1.6) для нахождения N _2..[1]. Эти уравнения в рассматриваемой задаче имеют вид:

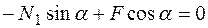и . Откуда

и .

Знак минус показывает, что направление усилия в стержне 2 противоположно показанному на рис. 1.6, т. е. стержень 2 сжат.

Определим напряжения по (1.1) и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче это будет стержень 1).

Из условия прочности этого стержня получим значение допускаемой нагрузки:

, .

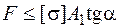Найдем перемещение узла С, построив план перемещений (рис. 1.7). Предварительно найдем абсолютные деформации стержней D l ₁и D l ₂ по формуле (1.3). В рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему конструкции в масштабе и отложим отрезки D l ₁ и D l ₂ вдоль оси каждого стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений была наглядной. В процессе деформации стержни поворачиваются относительно точек А и В по дугам. Из-за малости деформаций эти дуги заменяем касательными, т. е. перпендикулярами к направлениям стержней (отрезк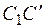и и 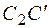на рис. 1.7). На пересечении дуг (перпендикуляров к направлениям стержней) находится новое положение узла C после деформации – точка 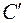на рис. 1.7. Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных геометрических выкладок.

Рис. 1.7. План перемещений

Примечание. Если конструкция имеет абсолютно жесткий стержень, то принцип построения плана перемещений тот же. Все точки абсолютно жесткого стержня могут перемещаться только по дугам (перпендикулярам к направлению стержня), поворачиваясь вокруг неподвижного шарнира. Например, если стержень АС на рис. 1.7 считать абсолютно жестким, то точка С переместится в положение и горизонтальное перемещение узла С будет равно нулю.

Дата добавления: 2014-12-08