Типы диэлектриков. Поляризация диэлектриков

Все вещества по электропроводности разделяются на проводники и диэлектрики. Промежуточное положение между ними занимают полупроводники.

Проводниками называют вещества, в которых имеются свободные носители зарядов, способные перемещаться под действием электрического поля. Примерами проводников являются металлы, растворы или расплавы солей, кислот, щелочей.

Диэлектриками или изоляторами называются вещества, в которых нет свободных носителей зарядов и которые, следовательно, не проводят электрический ток. Это будут идеаль­ные диэлектрики. В действительности диэлектрики проводят электрический ток, но очень слабо, их проводи­мость в 10¹⁵ -10²⁰ раз меньше, чем у проводников. Это обусловлено тем, что в обычных услови­ях заряды в диэлектриках связаны в устойчивые молекулы и не могут, как в проводниках, легко отрываться и становиться свободными. Молекулы диэлектрика электронейтральны: суммарный заряд электронов и атомных ядер, входящих в состав молекулы, равен нулю. В первом приближении молекулу можно рассматривать как диполь с электрическим моментом ; здесь q - заряд ядра молекулы, -век­тор, проведенный из "центра тяжести" электронов в "центр тяжести" положительных заря­дов атомных ядер.

Различают два основных типа диэлектриков: полярный и неполярный.

Диэлектрик называют неполярным, если в его молекулах в отсутствие внешнего электрического поля центры тяжести отрицательных и положительных зарядов совпадают, например, Для них диполный момент , т. к. . И, следовательно, суммарный дипольный момент неполярного диэлектрика .

В молекулах полярных диэлектриков (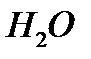, спирты, НС1...) центры тяжести зарядов раз­ных знаков сдвинуты друг относительно друга. В этом случае молекулы обладают собствен­ным дипольным моментом . Но эти дипольные моменты в отсутствие внешнего электрического поля из-за теплового движения молекул ориентированы хаотически и суммарный дипольный момент такого диэлектрика равен нулю, т. е.

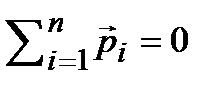
Если диэлектрик внести в электрическое поле, то в нем произойдет перераспределе­ние связанных зарядов. В результате этого суммарный дипольный момент диэлектрика становится отличным от нуля. В этом случае говорят, что произошла поляризация диэлектрика. Различают три типа поляризации диэлектриков:

1) ЭЛЕКТРОННАЯ: oна наблюдается в неполярных диэлек­триках, когда электронная оболочка смещается относитель­но ядра против поля.

2) ОРИЕНТАЦИОННАЯ: она наблюдается в полярных диэ­лектриках, когда диполи стремятся расположиться вдоль поля. Этому препятсятвует тепловое хаотическое движение.

3) ИОННАЯ: она наблюдается в твердых кристаллических диэлектриках, когда внешнее по­ле вызывает смещение положительных ионов по полю, а отрицательных - против поля.

Количественной мерой поляризации диэлектрика является поляризованность диэлек­трика - векторная величина, равная отношению суммарного дипольного момента малого объема диэлектрика к величине этого объема , т. е.

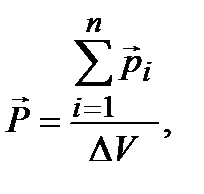(11-34)

в СИ Р измеряется в Кл / м².

Таким образом, вектор поляризованности диэлектрика равен дипольному моменту единицы объема поляризованного диэлектрика.

Как показывает опыт у изолированных диэлектриков вектор поляризованности для не слишком больших пропорционален напряженности электрического поля, т.е.

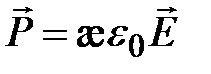, (11-35)

где 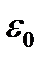- электрическая постоянная, æ - называется диэлектрической восприимчивостью ди­электрика; это безразмерная величина, которая для вакуума и, практически, для воздуха, ра­вна нулю(æ - каппа, греческая буква).

Итак, при внесении диэлектрика в электрическое поле с напряженностью происходит поляризация диэлектрика, в результате которой возникает поле связанных зарядов, направ­ленное против внешнего поля.

Напряженность поля связанных зарядов обозначим через 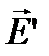; оказывается она пропорциональна напряженности поля в диэлектрике, т.е. поэтому напряженность поля в диэлектрике , или

откуда 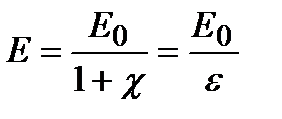(11-36) где 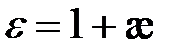(11-37)

называют относительной диэлектрической проницаемостью вещества или среды; 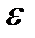- безразмерная величина; т.к. æ =0 для вакуума и, практически, для воздуха, для этих же сред 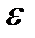= 1. Итак, поле в диэлектрике ослабляется в ε раз, по сравнению с полем в вакууме.

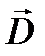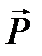11.9. Теорема Остроградского-Гаусса для поля в диэлектрике. Связь векторов - сме­щения, - напряженности и - поляризованности

ТеоремаОстроградского-Гаусса для потока вектора в вакууме имела вид:

, или

где Q - суммарный заряд, охватываемый замкнутой поверхностью S. В диэлектрике Q складывается из свободных (сторонних) зарядов и связанных зарядов, т.е.

(11-38)

Можно показать, что .

Подставляя эту формулу в (11-38), после преобразования получим (11-39)

Величину (11-40)

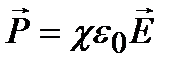называют вектором электрического смещения или вектором электрической индукции. Она измеряется, как и , в Кл/м². Учитывая, что находим

. (11-41)

Линии вектора могут начинаться или заканчиваться лишь на свободных зарядах, а линии - на свободных и связанных. С учетом (11-40) формула (11-39) запишется так

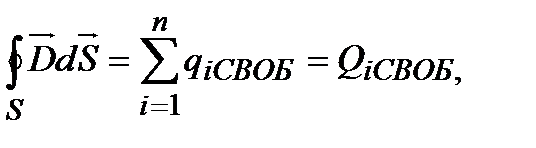, (11-41)

т.е. поток вектора электрического смещения через произвольную замкнутую поверхность S равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.

Это и есть теорема Остроградского-Гаусса в интегральной форме для поля в диэлек­трике, которая в дифференциальной форме выглядит так:

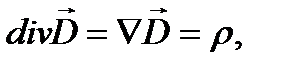
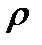= dq/dV, Кл / м (11-42)

ρ – объемная плотность свободных зарядов.

Дата добавления: 2014-12-08