
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функции нескольких переменных. Кратные интегралы
|
|
|
|
Неопределенный и определенный интегралы.
КОНТРОЛЬНАЯ РАБОТА № 3
Введение в математический анализ.
КОНТРОЛЬНАЯ РАБОТА № 2
Производная и ее приложения.
6.2.1–6.2.10. Найти пределы функций, не пользуясь правилом Лопиталя.
6.2.1. а) 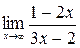 б)
б) 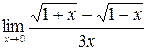
в)  г)
г) 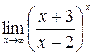
6.2.2. а)  б)
б) 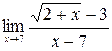
в) 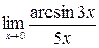 г)
г) 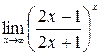
6.2.3. а)  б)
б) 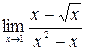
в) 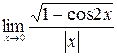 г)
г) 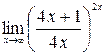
6.2.4. а) 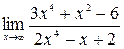 б)
б) 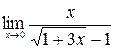
в) 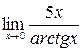 г)
г) 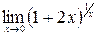
6.2.5. а) 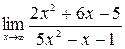 б)
б) 
в)  г)
г) 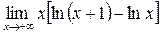
6.2.6. а) 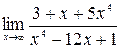 б)
б) 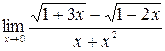
в) 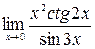 г)
г) 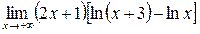
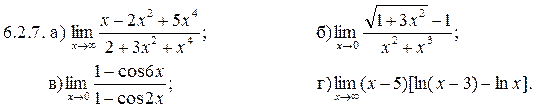
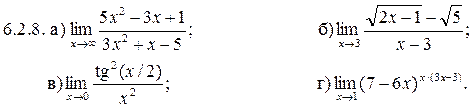
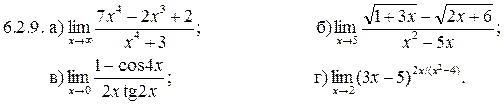
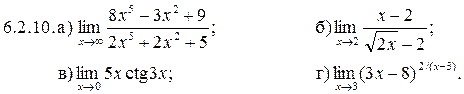
6.3.11–6.3.20. Задана функция у=f (х). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.
6.3.11. 
6.3.12. 
6.3.13. 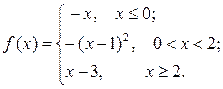
6.3.14. 
6.3.15. 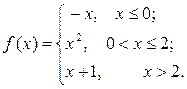
6.3.16. 
6.3.17. 
6.3.18. 
6.3.19. 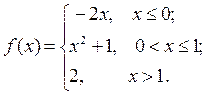
6.3.20. 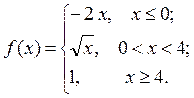
7.1.11–7.1.20. Найти производные 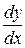 данных функций.
данных функций.
7.1.11. a) 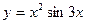 ; б)
; б) 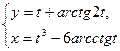 при
при  ;
;
в) 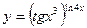 .
.
7.1.12. a) 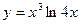 ; б)
; б) 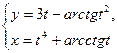 при
при 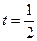 ;
;
в) 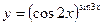 .
.
7.1.13. a) 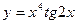 ; б)
; б) 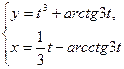 при
при  ;
;
в)  .
.
7.1.14. a) 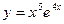 ; б)
; б) 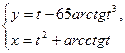 при
при 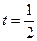 ;
;
в) 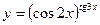 .
.
7.1.15. a)  ; б)
; б)  при
при  ;
;
в) 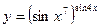 .
.
7.1.16. a) 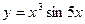 ; б)
; б) 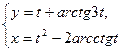 при
при  ;
;
в) 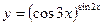 .
.
7.1.17. a) 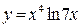 ; б)
; б) 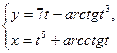 при
при 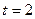 ;
;
в) 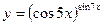 .
.
7.1.18. a) 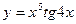 ; б)
; б) 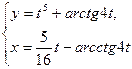 при
при 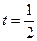 ;
;
в)  .
.
7.1.19. a)  ; б)
; б) 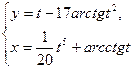 при
при 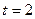 ;
;
в) 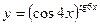 .
.
7.1.20. a) 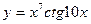 ; б)
; б) 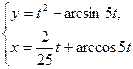 при
при 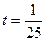 ;
;
в) 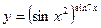 .
.
7.1.41–7.1.50. Найти пределы функции, применяя правило Лопиталя.


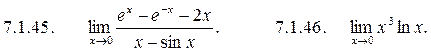


7.3.1–7.3.10. Исследовать методами дифференциального исчисления функцию 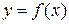 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
7.3.1. 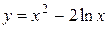 .
.
7.3.2. 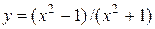 .
.
7.3.3. 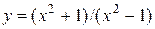 .
.
7.3.4. 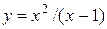 .
.
7.3.5. 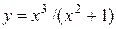 .
.
7.3.6. 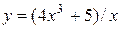 .
.
7.3.7. 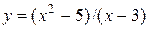 .
.
7.3.8. 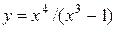 .
.
7.3.9. 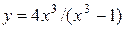 .
.
7.3.10. 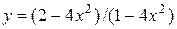 .
.
8.2.11–8.2.20. Найти неопределенные интегралы. В случаях а), б), в) результат проверить дифференцированием.
8.2.11.
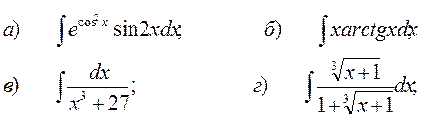
д) 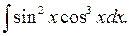 .
.
8.2.12.
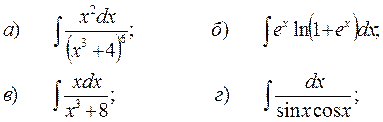
д) 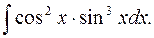
8.2.13.
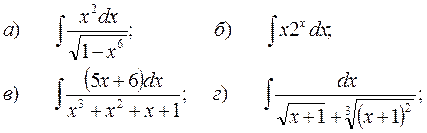
д) 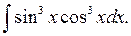
8.2.14.
а)  б)
б) 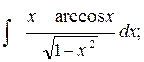
в) 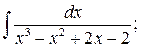 г)
г) 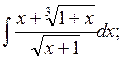
д) 
8.2.15.
а) 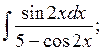 б)
б) 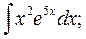
в) 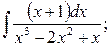 г)
г) 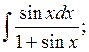
д) 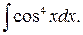
8.2.16.
а) 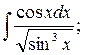 б)
б) 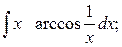
в) 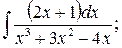 г)
г) 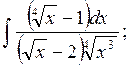
д) 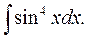
8.2.17.
а) 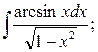 б)
б) 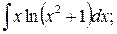
в) 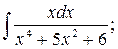 г)
г) 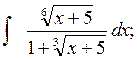
д) 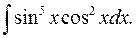
8.2.18.
а) 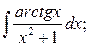 б)
б) 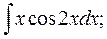
в)  г)
г) 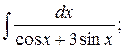
д) 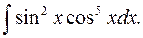
8.2.19.
а) 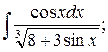 б)
б) 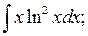
в) 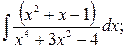 г)
г) 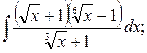
д) 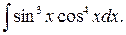
8.2.20.
а)  б)
б) 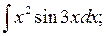
в) 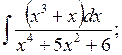 г)
г) 
д) 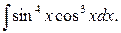
8.3.1–8.3.10. Вычислить несобственный интеграл или доказать его расходимость.
8.3.1. 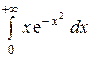 . 8.3.2.
. 8.3.2. 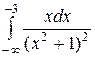 .
.
8.3.3. 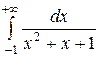 . 8.3.4.
. 8.3.4. 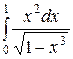 .
.
8.3.5. 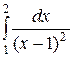 . 8.3.6.
. 8.3.6. 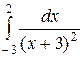 .
.
8.3.7. 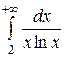 . 8.3.8.
. 8.3.8. 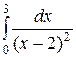 .
.
8.3.9.  . 8.3.10.
. 8.3.10. 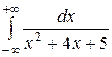 .
.
9.1.31–9.1.40. Дана функция двух переменных 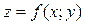 . Найти все
. Найти все
частные производные первого и второго порядков. Обосновать равенство 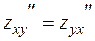 .
.
9.1.31.  . 9.1.32.
. 9.1.32. 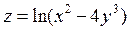 .
.
9.1.33. 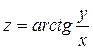 . 9.1.34.
. 9.1.34. 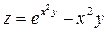 .
.
9.1.35. 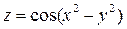 . 9.1.36.
. 9.1.36.  .
.
9.1.37.  9.1.38.
9.1.38.  .
.
9.1.39.  . 9.1.40.
. 9.1.40.  .
.
9.1.61–9.1.70. Вычислить двойной интеграл.
9.1.61. 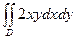 ; где область D – прямоугольник
; где область D – прямоугольник 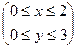 .
.
9.1.62.  ; где область D ограничена параболой
; где область D ограничена параболой 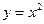 и прямыми
и прямыми 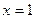 ,
, 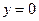 .
.
9.1.63.  ; где область D – прямоугольник
; где область D – прямоугольник 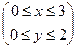 .
.
9.1.64. 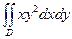 ; где область D – прямоугольник
; где область D – прямоугольник 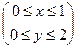 .
.
9.1.65. 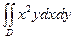 ; где область D – прямоугольник
; где область D – прямоугольник 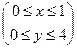 .
.
9.1.66.  ; где область D – прямоугольник
; где область D – прямоугольник 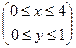 .
.
9.1.67. 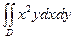 ; где область D ограничена параболой
; где область D ограничена параболой 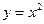 и прямыми
и прямыми 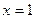 ,
, 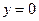 .
.
9.1.68. 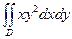 ; где область D ограничена параболой
; где область D ограничена параболой 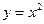 и прямыми
и прямыми 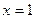 ,
, 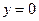 .
.
9.1.69. 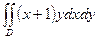 ; где область D – прямоугольник
; где область D – прямоугольник 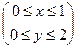 .
.
9.1.70. 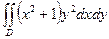 ; где область D – прямоугольник
; где область D – прямоугольник  .
.
9.2.21–9.2.30. Найти стационарные точки функции  и исследовать их на локальный экстремум.
и исследовать их на локальный экстремум.
9.2.21. 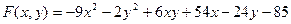 .
.
9.2.22. 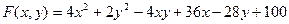 .
.
9.2.23. 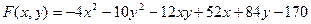 .
.
9.2.24. 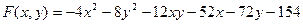 .
.
9.2.25. 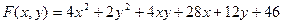 .
.
9.2.26. 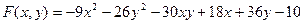 .
.
9.2.27.  .
.
9.2.28.  .
.
9.2.29.  .
.
9.2.30.  .
.
Задания на контрольные работы № 1 – 2
для студентов 1 курса заочной формы обучения направления
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 385; Нарушение авторских прав?; Мы поможем в написании вашей работы!