
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выбор критерия оптимальности
|
|
|
|
Постановка транспортной задачи
Транспортная задача (Т-задача) является одной из наиболее распространенных специальных задач ЛП. Первая строгая постановка Т-задачи принадлежит Ф. Хичкоку, поэтому в зарубежной литературе ее часто называют проблемой Хичкока.
Первый точный метод решения Т-задачи разработан Л. В. Канторовичем и М. К. Гавуриным.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления  (заводы, склады, базы и т.д.) в n пунктов назначения
(заводы, склады, базы и т.д.) в n пунктов назначения 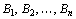 (магазины). При этом, из каждого пункта отправления (производства) возможно транспортировка продукта в любой пункт назначения (потребления). В качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
(магазины). При этом, из каждого пункта отправления (производства) возможно транспортировка продукта в любой пункт назначения (потребления). В качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
При решении транспортной задачи выбор критерия оптимальности имеет важное значение. Как известно, оценка экономической эффективности примерного плана может определятся по тому или иному критерию, положенного в основу расчета плана. Этот критерий является экономическим показателем, характеризующим качество плана. До настоящего времени нет общепринятого единого критерия всесторонне учитывающего экономические факторы. При решении транспортной задачи, в качестве критерия оптимальности в различных случаях используют следующие показатели:
1) Объем работы транспорта (критерий - расстояние в т/км). Минимум пробега удобен для оценки планов перевозок, поскольку расстояние перевозки определяется легко и точно для любого направления. Поэтому критерию нельзя решать транспортные задачи с участием многих видов транспорта. С успехом применяется при решении транспортных задач для автомобильного транспорта. При разработке оптимальных схем перевозки однородных грузов автомобилями.
2) Тарифная плата за перевозку груза (критерий - тарифы провозных плат). Позволяет получить схему перевозок, наилучшую с точки зрения хозрасчетных показателей предприятия. Все надбавки, а также существующие льготные тарифы затрудняют его использование.
3) Эксплутационные расходы на транспортировку грузов (критерий - себестоимость эксплутационных расходов). Более верно отражает экономичность перевозок различными видами транспорта. Позволяет делать обоснованные выводы о целесообразности переключения с одного вида транспорта на другой.
4) Сроки доставки грузов (критерий - затраты времени).

5) Приведенные затраты (с учетом эксплуатационных расходов, зависящих от размеров движения и капиталовложения в подвижной состав).
6) Приведенные затраты (с учетом полных эксплуатационных расходов капиталовложений на строительство объектов в подвижной состав).
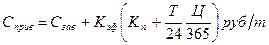 ,
,
где 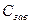 - эксплутационные издержки,
- эксплутационные издержки,
 -расчетный коэффициент эффективности капиталовложения,
-расчетный коэффициент эффективности капиталовложения,
 - капитальные вложения, приходящие на 1 т груза на протяжении участка,
- капитальные вложения, приходящие на 1 т груза на протяжении участка,
Т - время следования,
Ц - цена одной тоны груза.
Позволяет более полно производить оценку рационализации разных вариантов планов перевозок, с достаточно полной выраженностью количественно-одновременное влияние нескольких экономических факторов.
Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через 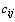 тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через
тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через 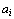 – запасы груза в i-м пункте отправления, через
– запасы груза в i-м пункте отправления, через 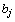 – потребности в грузе в j–м пункте назначения, а через
– потребности в грузе в j–м пункте назначения, а через 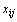 – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
– количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
 (1)
(1)
при условиях
 (2)
(2)
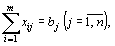 (3)
(3)
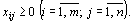 (4)
(4)
Поскольку переменные  удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), то обеспечиваются вывоз имеющегося груза из всех пунктов отправления, доставка необходимого количества груза в каждый из пунктов назначения, а также исключаются обратные перевозки.
удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), то обеспечиваются вывоз имеющегося груза из всех пунктов отправления, доставка необходимого количества груза в каждый из пунктов назначения, а также исключаются обратные перевозки.
Таким образом, Т-задача представляет собой задачу ЛП с m*n числом переменных, и m + n числом ограничений - равенств.
Очевидно, общее наличие груза у поставщиков равно 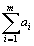 , а общая потребность в грузе в пунктах назначения равна
, а общая потребность в грузе в пунктах назначения равна 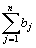 единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
 , (5)
, (5)
то модель такой транспортной задачи называется закрытой или сбалансированной.
Существует ряд практических задач, в которых условие баланса  не выполняется. Такие модели называются открытыми. Возможные два случая:
не выполняется. Такие модели называются открытыми. Возможные два случая:
1) 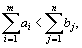
2) 
В первом случае полное удовлетворение спроса невозможно.
Такую задачу можно привести к обычной транспортной задаче следующим образом. В случае превышения потребности над запасом, т. е. 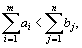 вводится фиктивный (m +1)–й пункт отправления с запасом груза
вводится фиктивный (m +1)–й пункт отправления с запасом груза  и тарифы полагаются равными нулю:
и тарифы полагаются равными нулю: 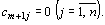
Тогда требуется минимизировать

при условиях
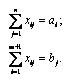
Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.
Рассмотрим теперь второй случай.
Аналогично, при  вводится фиктивный (n +1)–й пункт назначения с потребностью
вводится фиктивный (n +1)–й пункт назначения с потребностью 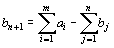 и соответствующие тарифы считаются равными нулю:
и соответствующие тарифы считаются равными нулю: 
Тогда соответствующая Т-задача запишется так:
Минимизировать 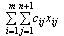
при условиях:
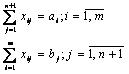
Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.
В дальнейшем будем рассматривать закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (5).
В некоторых случаях нужно задать, что по каким-либо маршрутам нельзя перевозить продукцию. Тогда стоимости перевозок по этим маршрутам задаются так, чтобы они превышали самые высокие стоимости возможных перевозок (для того, чтобы было невыгодно везти по недоступным маршрутам) – при решении задачи на минимум. На максимум – наоборот.
Иногда нужно учесть, что между какими-то пунктами отправки и какими-то пунктами потребления заключены договора на фиксированные объемы поставки, то надо исключить объем гарантированной поставки из дальнейшего рассмотрения. Для этого объем гарантированной поставки вычитается из следующих величин:
· из запаса соответствующего пункта отправки;
· из потребности соответствующего пункта назначения.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1216; Нарушение авторских прав?; Мы поможем в написании вашей работы!