Решение: Ошибка! Ошибка связи

Дополнительные материалы включают ряд презентаций, связанных с региональным компонентом курса, а именно с историей развития химического образования и науки на Дальнем Востоке России.

ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ

ШколА ЕСТЕСТВЕННЫХ НУК ДВФУ

по дисциплине «История и методология химии»

020101.65 - «Химия»

г. Владивосток

РАЗРАБОТАНО:

Профессор Кондриков Н.Б.

УТВЕРЖДЕНО:

Заведующий кафедрой Кондриков Н.Б.

№ п/п		Стоимость	Время эксплуатации (лет)	Расчетные величины
Тип самолета	Остаточная стоимость	Цена ремонта
	Самолет1	50 000,00р.		37 500,00р.	6 375,00р.
	Самолет2	60 000,00р.		48 000,00р.	5 760,00р.
	Самолет3	70 000,00р.		59 500,00р.	7 140,00р.
	Самолет4	80 000,00р.		64 000,00р.	7 680,00р.
	Самолет5	90 000,00р.		67 500,00р.	11 475,00р.
	Самолет6	100 000,00р.		90 000,00р.	10 800,00р.
	Самолет7	110 000,00р.		71 500,00р.	12 155,00р.
	Самолет8	120 000,00р.		72 000,00р.	12 240,00р.
	Самолет9	130 000,00р.		71 500,00р.	12 155,00р.
	Самолет10	140 000,00р.		112 000,00р.	13 440,00р.
	Самолет11	150 000,00р.		67 500,00р.	11 475,00р.
	Самолет12	160 000,00р.		144 000,00р.	17 280,00р.

Фрагмент таблицы в режиме формул:

Задание №4. Логические функции, блок 2. Вариант 19

Рассчитать таблицу значений составной функции, вычислить сумму ее значений на заданном интервале с заданным шагом и построить график (точечную диаграмму) функции.

Интервал изменения аргумента X:

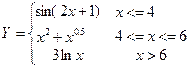
			Начальное
			Конечное
			Шаг	0,2

Решение:

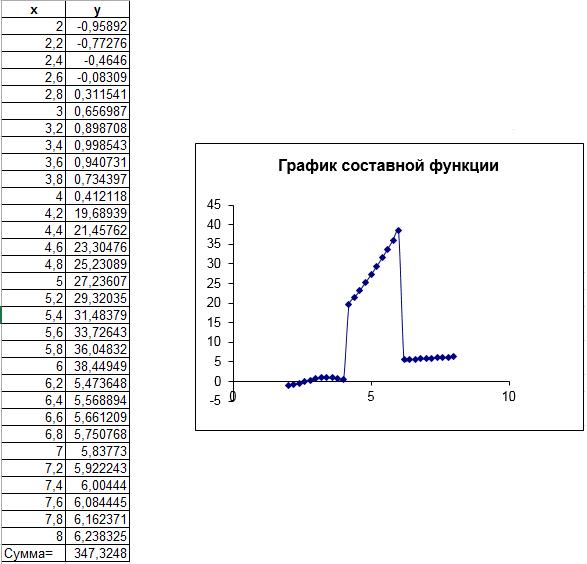
Формула для расчета составной функции на рисунке – в строке формул.

Сумма вычислялась автосуммированием, значение суммы отформатировано влево.

Задание №5. Система линейных уравнений. Вариант 29

Найти решение системы линейных уравнений методом «Обратной матрицы», выполнив задание, состоящее из следующих пунктов:

· Ввести матрицу коэффициентов при неизвестных и правые части.

· Решить систему линейных уравнений методом «Обратной матрицы».

Дана система линейных уравнений:

x₁+2x₂ – x₃ = 0

x₂+ x₃– x₄ = 1

x₁ +x₂ +x₃+x₄ = 13

x₁ + 2x₂–x₄ = 6

Порядок решения:

· Записать матрицу коэффициентов системы уравнений (размерность 4х4) и матрицу правых частей (размерность 4х1). Отсутствующие коэффициенты при неизвестных равны нулю.

· При помощи функции МОБР (А2:D5) вычисляется матрица, обратная матрице коэффициентов уравнений.

· При помощи функции МУМНОЖ выполняется умножение обратной матрицы на матрицу правых частей системы уравнений. Формула видна на рисунке в строке формул. Результат выполнения этой операции – матрица размерностью 4х1 – является решением системы линейный уравнений.

Матрица коэффициентов при неизвестных				Правые части
1,3	1,5	-3			-5
1,4		-3	1,5
2,2	-8	-2			-3
2,5	1,5	-4	2,5		-1
Обратная матрица	Значения неизвестных
1,875	12,29167	8,333333	-14,79166667	x1=
5,96E-18	0,666667	0,333333	-0,666666667	x2=
-0,3125	3,0625		-3,3125	x3=
-2,375	-7,79167	-5,33333	10,29166667	x4=

Задание №6. Аппроксимация. Вариант 25

Постановка задачи:

Найти аналитическую формулу зависимости Y_i от X_i в виде параболы

Y_p = a*x² +b*x+c методом наименьших квадратов.

Исходные данные:

X	0,5		1,5
Y

Решение:

Порядок действий:

• Формируем таблицу для вычисления коэффициентов и правых частей системы уравнений.
• Решаем систему уравнений методом обратной матрицы.
• Рассчитываем табличку для построения графиков. На график для наглядности помещаем исходный набор точек (Y) и сплошную линию, рассчитанную по формуле полученного полинома (Y_p).

Решение задачи:

	Задание	Расчетные величины
№ точки	x	y	x^2	x^3	x^4	x^2^y	x*y
	0,5		0,25	0,125	0,0625	3,75	7,5
	1,5		2,25	3,375	5,0625	31,5
сумма			7,5	12,5	22,125	96,25	67,5
Матрица коэффициентов			Правые части		Данные для построения графиков
22,125	12,5	7,5		96,25	x	y	yp
12,5	7,5			67,5	0,5		11,65306122
7,5		1,5					17,44897959
					1,5		16,74829932
							9,551020408
Обратная матрица			Ответы
0,598639	-0,81633	-0,27211	a=	-12,9932
-0,81633	1,004082	0,734694	b=	31,08163
-0,27211	0,734694	-0,42177	c=	-0,63946

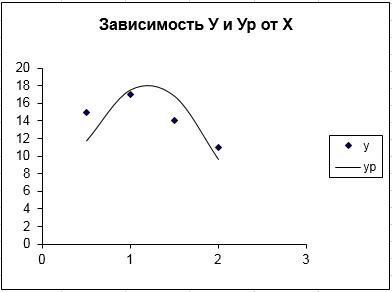
Набор заданных точек приближенно описывается функцией:

Y_р = -12,9932x²+31,08163x+(-0,63946)

Дата добавления: 2014-12-08