Предел функции в точке. Значение функции в точке

Значение функции в точке.

Пусть f(x)=x² +x+1

Если х=1, то f(x)= f(1)=1² +1+1=3 – в т.х=1 функция принимает соответствующее значение f(x)=3, аналогично

Если х=0, то f(x)= f(0)=0² +0+1=1

Если х=10, то f(x)= f(10)=10² +10+1=111

Рассмотрим данную функцию f(x)=x² +x+1 в окрестности т.х=1

х	у
0,95	2,8525
0,96	2,8816
0,97	2,9109
0,98	2,9404
0,99	2,9701
1,01	3,0301
1,02	3,0604
1,03	3,0909
1,04	3,1216
1,05	3,1525

Если значения аргумента х достаточно близко подходят к 1 с обеих сторон, то соответствующее значение функции как угодно близко приближается к числу 3

Обозначают х → 1, то у → 3 или

если (если разность между значением х и 1 ничтожно мала, то и разность между f(x) и 3 тоже сколь угодно мала), т.е.

| x-1 | < d, | f(x) – 3 | < ε,

где d,ε>0 очень малые числа d,ε→ 0

или: из того что 1-d<x< 1+d следует. что 3-ε<f(x)<3+ε, другими словами

– как только х попадает в d-окр.т.1 (1-d;1+d), то f(x) попадает в ε-окр.т.3(3-ε;3+ε) (см. табл. для d=0,01соотв ε)

Пусть х=1, соответствующее значение у=3

d=0,01 х = х -d =0,99, тогда у=2,9701 ε =0,0299

х = х+d=1,01, тогда у=3,0301 ε =0,0301, т.е. как только хÎ(0,99;1,01), то уÎ(2,9701; 3,0301)

Предел функции f(x) в точке х=1 равен 3:

lim f(x)=3

x→1

Функция может иметь предел даже в точках, в которых она не определена

Рассм. - в точке х=1 она не сущ, однако в точках близких к 1 ее значения будут равны и ее предел в точке х=1 равен 3 (при х → 1, f(x) → 3)

О: Число b называется пределом функции f(x) при х→а, если для любого сколь угодно малого положительного числа ε найдется такое малое положительное число d(ε), что для всех х из d-окрестности

т. а (а-d; а+d) или |x-а|<d выполняется условие |f(x–в|<ε и записывается: lim f(x)=в

x→а

Геометрический смысл предела функции в точке

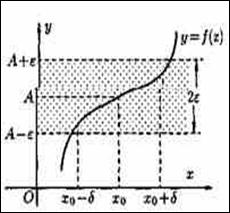
Пусть lim f(x)=А, это означает, что

x→х₀

, при условии |x-х₀|<d, выполняется | f(x) –А| < ε, т.е.

Как только значения аргумента х→х₀ попадают в d-окрестность точки х_0, т.е. (х₀-d; х₀+d) (или |x-х₀|<d), то соответствующие значения функции f(x) попадают в ε-окрестность.точки А, т.е.(А-ε;А+ε)(или | f(x) –А| < ε )

Свойства пределов функций:

1) предел от числа – равен самому числу : lim с=с

x→а

2) функция не может иметь двух пределов в одной точке

(напремер, у=1/х в т.х=0)

lim (1/x)= + ¥ lim (1/x)= - ¥, в т.х=0 предел для1,х не сущ

x→+0 x→-0

3) если каждая из функций f(x) и g(x) имеют предел в точке а, то в этой точке существуют пределы их алгебраической (±) суммы, произведения и частного, при этом числовой множитель выносится за знак предела, т.е.

пусть lim(f(x)=a и lim g(x)=b. тогда

x→а x→а

А) lim(f(x)± g(x))= lim f(x) ± lim g(x)=a±b

x→а x→а x→а

б) lim(f(x)× g(x))= lim f(x) × lim g(x)=a×b

x→а x→а x→а

в) lim(f(x)/ g(x))= lim f(x) / lim g(x) =a/b при lim g(x)¹0

x→а x→а x→а x→а

г) limk f(x))=k lim f(x)

x→а x→а

(Дополнительный материал)

Бесконечно малая и бесконечно большая функции

О: Функция называется бесконечно малой в окрестности точки x₀, если

(БМф)

О: Функция называется бесконечно малой на бесконечности, если

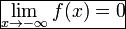
(БМф) или

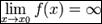О: Функция называется бесконечно большой в окрестности точки x₀, если

(ББф)

О: Функция называется бесконечно большой на бесконечности, если

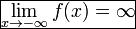
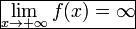(ББф) или

Свойства ББ и БМ функций:

1) Сумма или произведение бесконечно малых функций – функция бесконечно малая

2) Сумма или произведение бесконечно больших функций – функция бесконечно большая

3) При умножении на число БМф (ББф) – получается БМф (ББф)

4) Если f(x) - ББф, то обратная к ней функция - есть БМф, и наоборот, если f(x) - БМф, то обратная к ней функция - есть ББф

5) 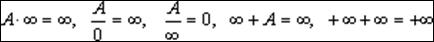простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0 – постоянное число

Вычисление пределов функций

1)

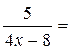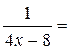2) lim 5 lim 5×lim 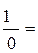[т.е.1 / БМф = ББф]= 5×¥ = ¥

x→2 x→2 x→2

ТИПЫ НЕОПРЕДЕЛЕННОСТЕЙ И СПОСОБЫ ИХ РАСКРЫТИЯ

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.

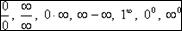
- данные условные выражения характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.

Рассмотрим некоторые приемы раскрытия неопределенностей.(, )

Для раскрытия неопределённостей типа используется следующий алгоритм:

· Выявление старшей степени переменной;

· Деление на эту старшую степень переменной как числителя, так и знаменателя.

Для раскрытия неопределённостей типа существует следующий алгоритм:

· Разложение на множители числителя и знаменателя;

· Сокращение дроби.

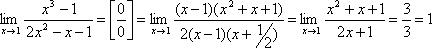
1)

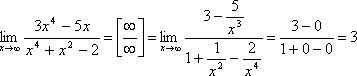
2)

3)

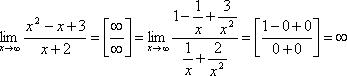
4)

5)

Техника вычисления пределов

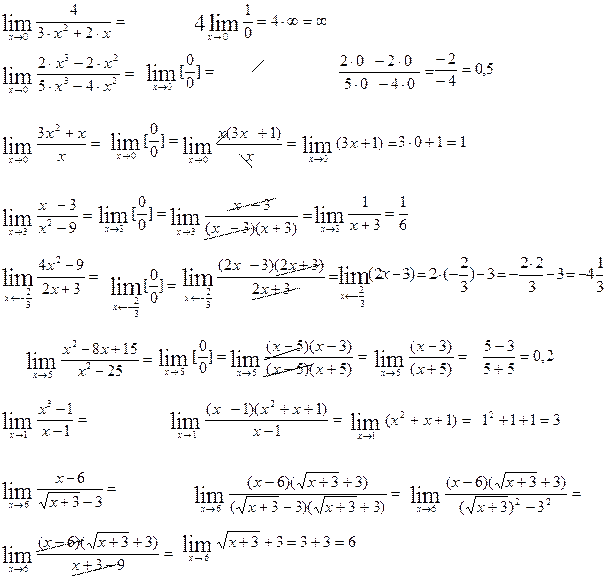
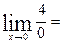
1)

2)

3)

4)

5)

6)

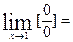
7)

8)

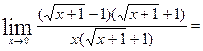
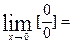
9)

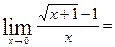
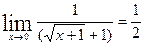
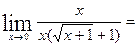
10)

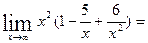11)

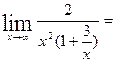
12)

13)

14)

15)

Дата добавления: 2014-12-08