Лекальные кривые

Практическая работа № 9

Все множество плоских кривых можно разделить на циркульные и лекальные. Циркульной называют кривую, которую можно построить с помощью циркуля. К ним относятся окружность, овал и т.д.

Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.

Лекальные кривые можно разделить на закономерные и незакономерные.

Закономерными называют кривые, которые можно задать алгебраическим выражением. Незакономерные кривые нельзя задать алгебраическим выражением.

Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.

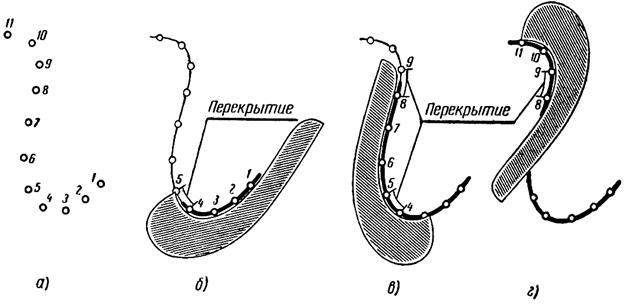
Лекальная кривая – это плавная кривая линия. Лекальную кривую нельзя даже частично провести с помощью циркуля. Лекальные кривые чертят с помощью лекал.

Рассмотрим построение лекальных кривых на примере Эллипса и Спирали Архимеда.

Эллипс – это замкнутая кривая. Его большая и малая оси есть оси симметрии эллипса. Точки F1 и F2 - это фокусы эллипса. Сумма расстояний от любой точки эллипса (от М, от N,...) до фокусов F1 и F2 есть величина постоянная. Она равна большой оси АВ. Например, F1M + F2M. = AB; F1N + F2>N=AB (рис. 17). Пример построения эллипса приведен на рис.2.

.

Рис. 1. Лекальная кривая – эллипс

Задание: Выполнить чертеж лекальных кривых (эллипс, спираль Архимеда) на формате А4. Размеры даны в задачах (см. ниже). Название работы: Лекальные кривые.

Задача 1:

Построение лекальной кривой – эллипса

1.Даны большая ось АВ и малая ось CD эллипса

2. Проводим из центра О окружность радиуса ОА и окружность радиуса ОС.

3. Делим большую окружность на 12 равных частей. Точки деления 1, 2, 3, 12 окружности соединяем с центром О. Прямые 1-7, 2-8... 6-12 делят малую окружность тоже на 12 равных частей.4. Из точек деления большой окружности проводим прямые параллельные CD. Из точек деления малой окружности проводим прямые, параллельные АВ. Точки пересечения вертикальных и горизонтальных прямых – это искомые точки эллипса. 5. Соединяем точки плавной кривой с помощью лекал (рис.2.).

Примечание: для выполнения данной задачи взять исходные данные: АB=70, СD=40, окружность разделить на 24 части.

Рис. 2. Построение лекальной кривой – эллипса

Спиралью Архимеда называется плоская кривая, полученная как след точки, движущейся равномерно поступательно от неподвижной точки О по выходящему из нее и равномерно вращающемуся вокруг точки О лучу (радиусу)Точка О называется полюсом спирали; отрезок ОА называется шагом t спирали; отрезок KL – нормалью спирали, а прямая MN, перпендикулярная к нормали, называется касательной; точка К может находиться в любом месте спирали, а точку L находят путем построения, для чего точку К соединяют прямой с точкой О и в точке О проводят перпендикуляр к отрезку КО, который пересечет в точке L окружность, проведенную из центра О диаметром D = t/3,14.

Задача 2:

Построение Архимедовой спирали

Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей. Из конца О отрезка / проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.

На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т.д.

После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую – спираль Архимеда.

Примечание: для выполнения задания на формате А4 взять следующие значения: R=t=55, окружность разделить на 12 частей.

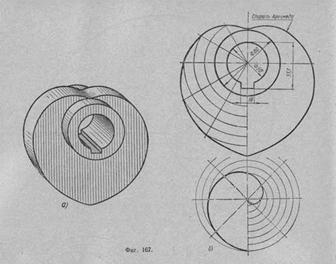
На рисунке дано изображение распределительного кулачка. Очертания боковых сторон его выполняют по спирали Архимеда.

Дата добавления: 2014-12-10