Политропный процесс

Основные термодинамические процессы идеальных газов

ЛЕКЦИЯ 4

ТД анализ любой системы состоит в следующем:

1. Выявить уравнение процесса. 2. Установить аналитическую взаимосвязь между

параметрами состояния, (связь между параметрами p, v, T, S, т.е. уравнения: p=f₁ (v), T=f₂ (v), T=f₃ (p), S=f₄ (T)). 3. Рассчитать величину работы изменения объема рабочего тела.4. Рассчитать количество подведенной или отведенной теплоты. 5. Рассчитать уеличину изменения внутренней энергии. 6. Рассчитать величины изменения энтальпии рабочего тела.

1. Рассчитать величину изменения энтропии рабочего тела.

Политропными процессами наз. процессы, протекающие при постоянной теплоемкости и вызываемые подводом или отводом теплоты. Следовательно, в любом политропном процессе, распределение теплоты между значениями, характеризующими изменение внутренней энергии и работу газа, остается неизменным, т.е. отношение:

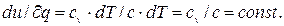
где с – постоянная для данного газа теплоемкость газа или

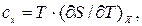т.е.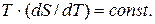

Для вывода уравнения обратимого политропного процесса идеального газа используем общее уравнение 1-го закона ТТД:

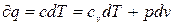, (4.1) или 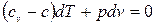, (4.2)

Воспользуемся характеристическим уравнением состояния газа (pv=RT), продифференцировав которое получим: рd v + v dp=RdT, т.е. dT=(pd v + v dp)/R

Решив совместно уравнения (4.1) и (4.2), получим: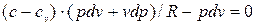

раскрыв скобки, получим: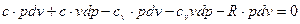

Сгруппировав слагаемые, содержащие произведения v dp и pd v, а также учитывая, что , после преобразований будем иметь: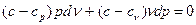

Разделив это равенство на (c-c_v), получим: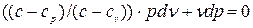

Обозначив через n дробь 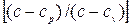получим: n pd v + v dp=0

Разделив это равенство на pv, после интегрирования и последующего потенцирования,

получим: ; ;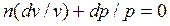

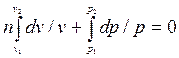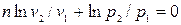
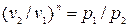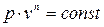; , (4.3)

Уравнение (4.3) носит название уравнения политропного процесса,

где: 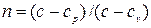- показатель политропы.

Показатель политропы может принимать любое численное значение в пределах от 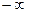до 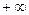, но для данного процесса он явл. величиной постоянной.

Связь между параметрами p, v, T, а именно:

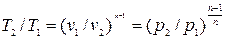, (4.4) 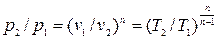, (4.5)

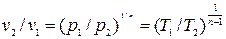, (4.6)

Работа политропного процесса.

Поскольку работа изменения объема газа в любом процессе выражается уравнением 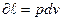, то для политропного процесса в соответствии с уравнениями политропы, имеем: 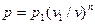, следовательно:

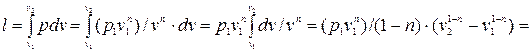(4.7)

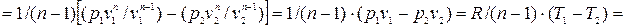
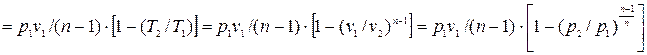Количество теплоты, подводимой к системе (или отводимой от нее) в политропном процессе, определяется следующим образом:

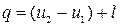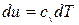т.к. , и 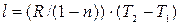то получаем:

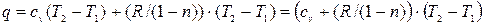
но 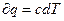т.е. q=c (T₂-T₁) и следовательно

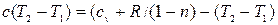после преобразований (учитывая, что 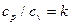), имеем: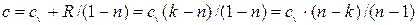

Откуда:

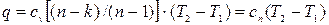(4.8)

где 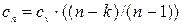- теплоемкость идеального газа в политропном процессе.

При с_v, k, n=const поэтому и с_n=const, т.е. политропный процесс иногда определяют как процесс с постоянной теплоемкостью.

Изменение внутренней энергии равно: 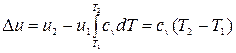, (4.9)

Изменение энтальпии равно: 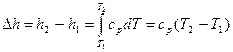, (4.10)

Изменение энтропии в политропном процессе:

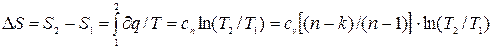, (4.11)

При движении газа в потоке располагаемая работа его в политропном процессе равна:

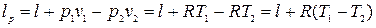(4.12)

Дата добавления: 2014-11-29