Теоретичні відомості. Тверді тіла під час нагрівання збільшують свій об’єм

Тверді тіла під час нагрівання збільшують свій об’єм. Це – теплове розширення. Очевидно, що об’єм кристала зростає із збільшенням середньої відстані між атомами. Чим же зумовлене збільшення відстані між атомами кристала під час нагрівання? Розглянемо криву залежності енергії взаємодії частинок твердого тіла від віддалі між ними (рис.12). Під час абсолютного нуля частинки знаходяться на віддалях 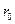, одна від одної, що відповідає мінімуму енергії взаємодії (на дні «потенціальної ями» ), Ці віддалі визначають розмір тіла під час абсолютного нуля. З підвищенням температури частинки починають коливатись біля положення рівноваги 0. Для спрощення припустимо, що частинка 1 нерухома, а коливається лише частинка 2, а її кінетична енергія досягає найбільшого значення 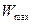у момент проходження частинкою положення рівноваги 0.

На рис. 12 енергію 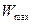відкладено вверх від дна потенціальної яма. Під час руху частинки 2 вліво від положення рівноваги, кінетична енергія витрачається на подолання сил відштовхування її від частинки 1 та переходять в потенціальну енергію взаємодії частинок. Відхилення вліво відбувається до тих пір, поки вся кінетична енергія частини 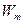не перейде в потенціальну енергію. Остання збільшиться на 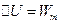і дорівнюватиме – (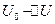), а частинка 2 зміститься максимально вліво на віддаль 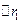. Під час руху частинки 2 вправо від положення рівновага кінетична енергія витрачається на подолання сил притягання її до частинки 1 й також переходить у потенціальну енергію взаємодії цих частинок. У точці в, що знаходиться на віддалі 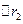від положення рівноваги, вся кінетична енергія 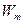переходить у потенціальну, внаслідок чого, остання збільшується на 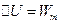r і отримає значення - .

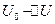Якби частинка 2 здійснювала суто гармонічні коливання, то сила , що виникає під час відхилення її від положення рівноваги на віддаль , була б строго пропорційна величині цього відхилення й направлена до положення рівноваги:

. (1)

Зміну потенціальної енергії частинки 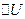можна було б описати під час цього параболою 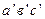(рис. 12), тобто рівнянням:

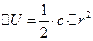. (2)

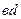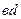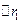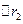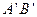Ця парабола симетрична відносно прямої , паралельної до осі координат, що знаходиться на віддалі від . Тому відхилення та були б однаковими за величиною (віддалі та ) й середина розмаху збігалася б із положенням рівноваги 0. Нагрівання тіла в цьому разі не могло спричинити його розширення, оскільки із збільшенням температури відбувалося б лише збільшення амплітуди коливань частинок, а середні віддалі між ними лишались незмінними.

Насправді ж потенціальна крива , як видно з рис.12, є несиметричною відносно прямої 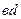: її ліва частина 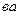піднімається крутіше від правої частини . Це означає, що коливання частинок у твердому тілі є ангармонічними. Для врахування асиметрії потенціальної кривої в рівняння (2) вводиться додатковий член і рівняння (2) набуває вигляду:

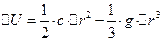, (3)

де - коефіцієнт пропорціональності.

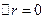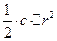Під час відхилення частинки 2 вправо () член віднімається від й частина йде пологіше від частини ; під час відхилення вліво (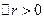) член додається до 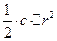і частина 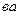йде крутіше від частини .

Рис.11.

Несиметричний характер потенціальної кривої призводить до того, що відхилення частинки 2 вправо і вліво є неоднаковими: вправо частинка відхиляється сильніше, ніж вліво (див. рис. 11). Внаслідок цього середнє положення цієї частинки (точка 0) вже не збігається з положенням рівноваги 0, а зміщується вправо від нього на віддаль 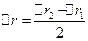. Це відповідає збільшенню середньої віддалі між частинками 1 і 2 на величину .

Таким чином, під час нагрівання тіла середні віддалі між частинками повинні збільшуватись і тіло повинно розширятись. Причиною цьому є ангармонічний характер коливань частинок твердого тіла, що призводить до асиметрії кривої лінійної залежності енергії взаємодії частинок від віддалі ніж ними.

Розрахунок показує, що під час нагрівання тіла до температури Т середні віддані ніж частинками збільшуються на величину , яка визначається за формулою:

,

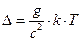де 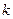- стала Больцмана.

Відносне лінійне розширення тіла чисельно дорівнює відношенню зміни середньої віддалі між частинками до нормальної віддалі між ними 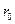, пропорційне абсолютній температурі тіла й дорівнює:

.

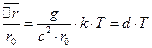Коефіцієнт пропорційності є коефіцієнтом лінійного розширення тіла. Підстановка числових значень 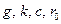дає для 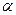величину порядка 10^-4—10^-5, що добре узгоджується з дослідом. Дослід підтверджує також, що під час достатньо високих температурах розширення тіла пропорційне його абсолютній температурі, а коефіцієнт розширення 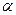не залежить від температури. Однак, в області низьких температур коефіцієнт лінійного розширення 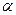зменшується із зменшенням температури й під час наближення її до абсолютного нуля прямує до нуля.

Практично коефіцієнт лінійного розширення визначають із співвідношення:

, (4)

де 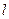початкова довжина тіла, 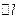- видовження до зміни температури на .

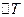Тобто коефіцієнт лінійного розширення дорівнює відносній зміні його довжини до зміни температури на 1ºС.

Коефіцієнт об’ємного розширення визначається формулою:

, (5)

і дорівнює відносній зміні об’єму 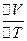, віднесеній до 1 град. З (4) і (5) випливає, що довжина і об’єм за деякої температури, яка відрізняється від початкової на 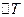градусів, виражаються формулою (за деякого ) ;

,

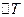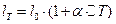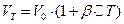де - початкові довжини та об’єм тіла.

Внаслідок анізотропії кристалів коефіцієнт лінійного розширення 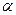є різним у різних напрямках. Це означає, що коли з даного кристалу виточити кулю, то після її нагрівання вона втратить сферичну форму. У найзагальнішому випадку така куля під час нагрівання перетвориться в тривісний еліпсоїд, осі якого зв’язані з кристалографічними осями кристала. Для кристалів з кубічною симетрією, як і для ізотропних тіл, 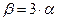. Коефіцієнт лінійного й об’ємного розширення практично залишаються сталими, якщо інтервали температур, у яких їх вимірюють, малі, а самі температури високі. Взагалі коефіцієнти теплового розширення залежать від температури й притому так само, як теплоємність, тобто під час низьких температур коефіцієнти 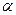і зменшуються із зниженням температури пропорційно кубу температури, прямуючи, як і теплоємність, до нуля за абсолютного нуля. Це не дивно, бо і теплоємність, і розширення пов’язані з коливаннями ґратки. Теплоємність дає кількість теплоти, необхідну для збільшення середньої енергії теплових коливань атомів, яка залежить від амплітуди коливань, а коефіцієнт теплового розширення безпосередньо пов’язаний з середніми відстанями між атомами, які також залежать від амплітуди атомних коливань. Звідси випливає важливий закон, відкритий Грюнейзеном: відношення коефіцієнта теплового розширення до атомної теплоємності твердого тіла для даної речовини є величина стала (тобто така, що не залежить від температури).

Дата добавления: 2014-12-10