Розв’язання. Ідентифікуємо змінні:

Ідентифікуємо змінні:

Y - витрати на харчування (залежна змінна);

Х (х₁, х₂) - незалежні змінні: х₁ - загальні витрати, г.о.; х₂ - розмір сім'ї (кількість членів сім'ї).

Практикою спостережень, наприклад, встановлено, що дана модель може бути специфікована у лінійній формі:

де Y, 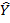- відповідно фактичні та розрахункові значення тижневих витрат на харчування за моделлю; u - залишки; 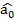, ₁, ₂ - оцінка параметрів моделі.

Оператор оцінки параметрів моделі а}- при використанні 1МНК має вигляд:

Х΄- матриця, транспонована до Х.

Одиниця в матриці незалежних змінних X дописується тоді, коли економетрична модель має вільний член а₀ (як у нашому випадку).

Згідно з оператором оцінювання обчисляємо матриці:

Отже, економетрична модель множинної регресії для тижневих витрат на харчування запишеться так:

Зробимо економетричні висновки.

Коли за всіх однакових умов незалежна змінна х₁ (загальні витрати) змінюється (збільшується або зменшується) на одиницю, то залежна змінна У змінюється на 0,2 одиниць. Якщо при тих же умовах незалежна змінна х₂ (розмір сім'ї) змінюється на одиницю, то залежна змінна У змінюється на 6,97 одиниць.

Визначимо множинні коефіцієнти детермінації та кореляції:

№ з/п	У		( - ) ^2	(У - ) ^2	u = = У -	u^2 = = (У - ) ^2
	2				6
		20,3			1,7	2,89
		27,0
		39,0
		58,0
		42,9			4,1	16,81
		55,1			10,9	118,8
		69,9		18,5	11,1	123,2
		96,8	132.2		9,2	84,6
		66,1			3,9	15,21
		82,0	10,9	94,1
		104,6			14,4	207,4
		131,7			11,3	127,7
		95,0	94,1	59,3	-2
		119,6			13,4	179,6
		150,8			18,2	331,2
		202,0			-5
І		1364,8			-	1656,4
У середньому		85,3	-	-	-	-

Визначимо коефіцієнти детермінації та кореляції, якщо (n-1)=(16-1)=15 і (n-m₁)=(16-3)=13:

=0.950; R=0.975.

Коефіцієнти детермінації та кореляції наближені до одиниці, тому зв'язок між змінними X та У - тісний. Значення коефіцієнта витрат на харчування на 95% визначається варіаціями загальних витрат та розміром сім'ї, а 5% припадає на невраховані фактори.

Визначимо значимість зв'язку між змінними X та У за допомогою F-критерію Фішера

=

Обчислене фактичне значення критерія Фішера F порівнюється з табличним F_табл, (див. додаток А). При ступенях вільності чисельника (m₁-1)=(3-1)=2 та знаменника (n-m₁)=(16-3)=13 і прийнятому рівню довіри (1-α)=(1-0,05)=0,95 F_табл для розглянутої моделі дорівнює F_табл =3,81. Так як F>F_тавл (141,0>3,81), то це означає значимість зв'язку в економетричній моделі.

Для перевірки значимісті коефіцієнта кореляції R розраховуємо t-критерій Ст'юдента:

Звикористаннямстатистичнихтаблиць (додатокБ) прирівнізначимостіα =0,05 тачислуступеніввільності (n-m1)=(16-3)=13 вибираємо t_табл =1,771.

Оскільки t_α>t_табл, то можна зробити висновок про значимість коефіцієнта кореляції.

Для оцінки значимості оцінок параметрів моделі множинної регресії обчислимо t-критерій. Дисперсія залишокдорівнює

=

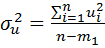Тоді з урахуванням стандартної помилки оцінки параметрів розраховуєм значення t-критеріїв:

Вище було визначене табличне значення t-критерію t_табл=1,771. Порівняння розрахованих та табличного значень t-критеріїв приводить до такого: t_1α <t_табл, що свідчить про нестійкість впливу змінної х₁ на результативну ознаку У; t_2α <t_табл. та t_3α <t_табл, що показує істотний зв'язок цих залежних змінних (х₂, х₃) на залежну У.

На основі t-критеріїв та стандартної помилки

можуть бути визначені довірчі інтервали для параметрів моделі:

Так як значення стандартних помилок S_aj не перевищують абсолютні значення оцінок параметрів _j, то цеозначає, що оцінки параметрів є незміщеними.

Нарешті, побудуємо точковий та інтервальний прогнози для економетричної моделі.

Визначимо прогнозне значення залежної змінної при

.

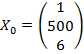Тоді М(Y₀) можна розглядати як оцінку прогнозного значення математичного сподівання та індивідуального значення витрат на харчування при відомих загальних витратах х₁ та розміру сім'ї х₂.

Получимо інтервальний прогноз математичного сподівання М(Y₀).

Визначимо для цього дисперсію прогнозну 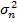з урахуванням матриці охибок (X`X)^-1, яка для розглядаємого прикладу має наведений вигляд:

Елементи дисперсійно-коваріаційної матриці за формулами мають значення:

Тоді дисперсіно-коваріаційна матриця запишеться у

вигляді:

Знайлемо дисперсію помилок: =

Стандартнапомилкапрогнозу математичногосподівання М():

Тоді інтервальний прогноз математичного сподівання М()буде вмежах:

Обчислимо дисперсію та стандартнупомилкупрогнозу індивідуального значення У₀:

Визначимо індивідуальний прогноз індивідуальногозначення У₀:

Отже, при 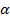=0,05 рівні довіри (1- 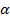)=0,95, що відповідає ймовірності р=0,95, прогноз математичного сподівання М(У₀) потрапляє в інтервал [103,8; 197,4], а прогноз індивідуального значення - в інтервал [99,8; 201,4]. В економічної інтерпретації це означає, що при прогнозних загальних витратах у 500 одиниць при сім'ї з шести осіб середні витрати на харчування потрапляють в інтервал103,8

Водночас окреміінтервальні витратимістяться в інтервали 99,8

Дата добавления: 2014-12-10