Предмет математической статистики 1 страница

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

В основе научных знаний лежат наблюдения за изучаемыми объектами и процессами, присущими данным объектам. Однако, ясно, что единичное наблюдение вряд ли позволит сразу установить свойства наблюдаемого объкта. Поэтому для установления свойств и связей изучаемого объекта его приходится наблюдать многократно, а затем результаты наблюдений обрабатывать и лишь после этого делать выводы.

В математической статистике изучаются случайные величины и системы случайных величин при помощи наблюдений. В связи с этим в математической статистике (которая достаточно долго развивалась независимо от теории вероятностей) случайные величины принято называть наблюдаемыми признаками.

Первичная обработка результатов измерений.

Пусть рассматривается некоторый наблюдаемый признак Х. Назовем генеральной совокупностью наблюдаемого признака Х множество значений, которые может принимать этот наблюдаемый признак.

Набор значений 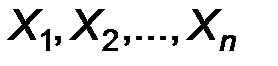, являющихся результатами наблюдений (измерений) наблюдаемого признака Х, назовем выборкой объема п из генеральной совокупности.

Отметим, что на выборку можно смотреть с двух точек зрения:

1. 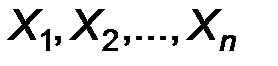-результаты измерений (конкретные числа),

2. 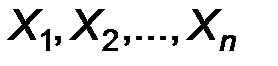- совокупность п случайных величин, имеющих такие же распределения как и наблюдаемый признак.

Разумеется, первой точки зрения на выборку придерживаются после проведения измерений, а второй – до проведения измерений.

В этом пункте мы будем рассматривать выборку как результаты наблюдений. Как правило, объем выборки весьма велик и это мешает увидеть закономерности, присущие наблюдаемому признаку. В связи с этим возникает задача о выборе сравнительно небольшого числа представителей выборки так, чтобы были сохранены основные закономерности, описываемые исходной выборкой. Процедура решения

этой задачи называется первичной обработкой результатов измерений. Первичная обработка проводится по-разному в зависимости от типа наблюдаемого признака.

1. Ранжирование.

Пусть наблюдаемый признак Х является дискретной СВ. В этом случае, как известно, генеральная совокупность представляет собой не более чем счетное множество. В таком случае, всякая выборка есть конечное подмножество этого множества. Под ранжированием понимают расположение в порядке возрастания значений, упомянутых в выборке, с указанием количества повторов каждого значения.

Поясним сказанное примером.

Пример. Пусть Х – количество сбоев станка в течении смены. В результате проведения наблюдений получены следующие данные:

5,1,3,2,4,1,2,3,4,5,3,2,2,1,2,5,4,4,4,3,1,2,3,4,5. Требуется провести первичную обработку результатов измерений.

В данном случае, очевидно, что наблюдаемый признак является ДСВ, поэтому первичная обработка есть ранжирование:

Х

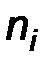
Значения 1,2,3,4,5, встречающиеся в приведенной таблице, называют вариантами, числа 4,6,5,6,4 – их частотами соответственно, а саму таблицу - вариационным рядом частот.

Отметим, что сумма частот 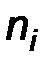совпадает с объемом выборки: 4+6+5+6+4=25.

Иногда вместо вариационного ряда частот используют вариационный ряд относительных частот, который отличается от вариационного ряда частот тем, что вместо частот 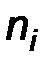используются относительные частоты 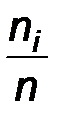. Ясно, что сумма относительных частот обязательно равна 1: .

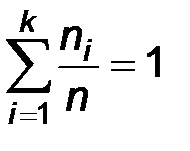В приведенном выше примере вариационный ряд относительных частот имеет вид:

Х
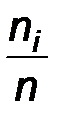
	0,16	0,24	0.20	0,24	0,16

2. Интервальная обработка выборки.

В этом пункте мы рассматриваем случай, когда генеральная совокупность не является дискретным множеством. Нашей целью является построение вариационных рядов, аналогичных рассмотренным выше. Достигается поставленная цель при помощи, описываемого ниже эмпирического алгоритма, называемого интервальной обработкой выборки.

По выборке 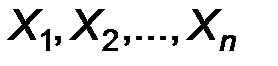объема п строят, так называемый интервальный ряд частот:

Х			………………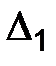
			………………

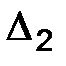
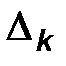
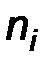
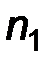
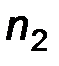
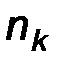
где 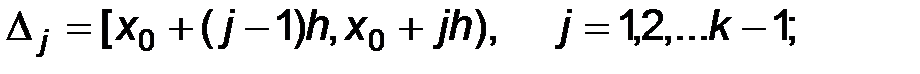а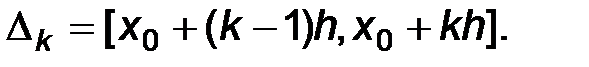

При этом число интервалов расчитывается по эмпирической формуле Стерджеса 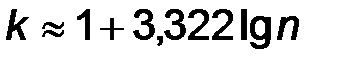, шаг h определяется по формуле 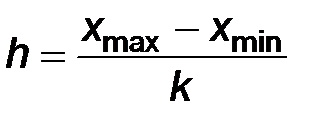, а через 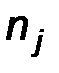обозначают число наблюдений, попавших в интервал 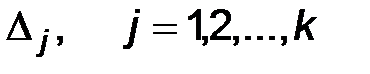. В качестве 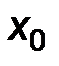рекомендуют выбирать .

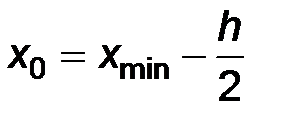После построения интервального ряда частот вариационный ряд частот получают из него, заменяя каждый из интервалов его одним представителем. Как правило, в качестве представителя интервала берут его середину.

Пример. Построить вариационный ряд частот и относительных частот по результатам измерений:

2,3; 2,5; 2,7; 2,35; 2,71; 2,32; 2,36; 2,44; 2,61; 2,67; 2,83; 2,86; 3,01; 3,12; 3,14; 2,61;2,49; 2,57; 2,52; 2,54; 3,03; 3,05.

Очевидно, в рассматриваемом случае п =25; 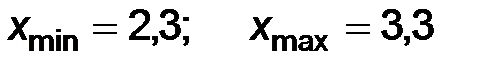, поэтому

.

Руководствуясь изложенными выше соображениями, строим интервальный ряд частот:

Х	[2,2; 2,4)	[2,4; 2,6)	[2,6; 2,8)	[2,8; 3,0)	[3,0; 3,2)	[3,2; 3,4]

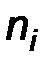
Заменяя интервалы их серединами, получаем вариационный ряд частот, а затем вариационный ряд относительных частот:

Х	2,3	2,5	2,7	2,9	3,1	3,3

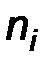
Х	2,3	2,5	2,7	2,9	3,1	3,3
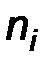
	0,16	0,24	0,2	0,08	0,24	0,08

Всюду ниже мы считаем, что первичная обработка результатов измерений произведена и выборка представлена в виде вариационного ряда частот или относительных частот.

Графическое изображение результатов измерений. Гистограмма. Полигон распределения

Гистограмма служит для графического изображения интервальных рядов и строится следующим образом: на оси абсцисс наносятся интервалы, в которых принимает значения наблюдаемый признак, а на оси ординат – частоты (относительные частоты) попадания наблюдаемого признака в соответствующий интервал. Гистограммой является ступенчатая фигура, ограничиваемая построенными таким образом прямоугольниками.

Для определенности будем считать, что задан интервальный ряд частот.

Х	[ , )	[ , )	…………	[ , ]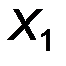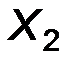
			…………

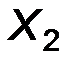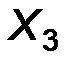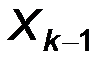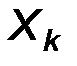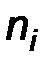
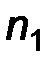
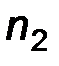
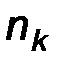
Тогда, согласно определению, данному выше, гистограмма этого интервального ряда имеет следующий вид:

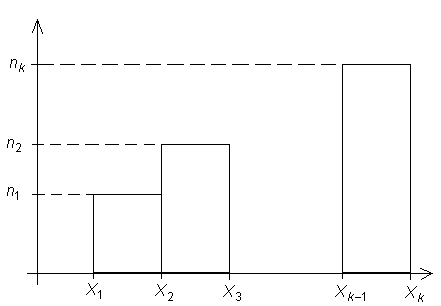
Вариационные ряды геометрически изображают при помощи полигонов частот или относительных частот. Пусть, для определенности, задан вариационный ряд частот

Х			…………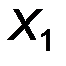
			…………

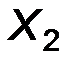
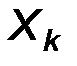
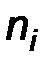
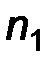
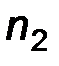
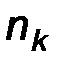
На плоскость наносят точки с координатами 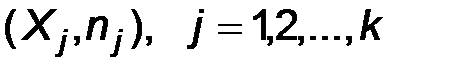и соединяют их ломаной. Крайние левую и правую точки соединяют с ближайшими точками вида 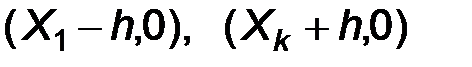, где h – шаг. Таким образом, полигон имеет следующий вид:

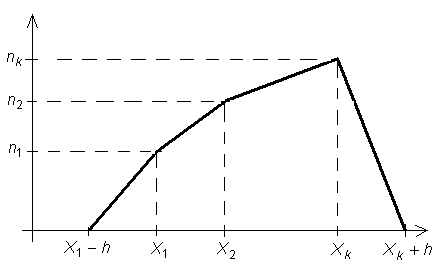
Замечание. Иногда для графического изображения вариационных рядов используют не полигоны, а, так называемые, куммулятивные кривые. Например, куммулятивная кривая частот есть ломанная, соединяющая точки 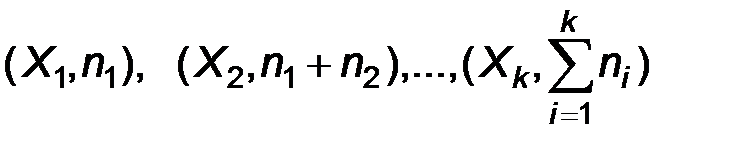. Аналогичным образом определяется куммулятивная кривая относительных частот.

Эмпирическая функция распределения. Эмпирические числовые характеристики.

Пусть наблюдаемый признак задан вариационным рядом относительных частот

Х			……………..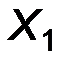
			……………..

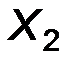
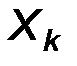
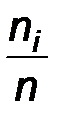
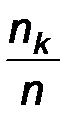
Поскольку 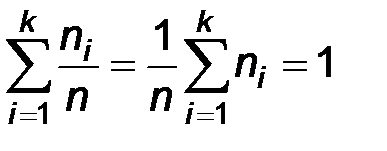, то вариационный ряд относительных частот является законом распределения для некоторой дискретной случайной величины 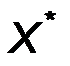. Случайную величину 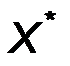называют эмпирической СВ, соответствующей рассматриваемой выборке наблюдаемого признака Х. Разумеется при изменении выборки эмпирическая СВ также меняется. Обозначим через 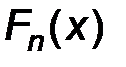функцию распределения СВ 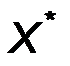, построенную по выборке объема п. Эту функцию называют эмпирической функцией распределения СВ Х. Эмпирическая функция распределения при неограниченном увеличении объема выборки в некотором смысле приближается к функции распределения наблюдаемого признака Х. Точнее, имеет место следующее утверждение.

Теорема Гливенко-Кантелли. Эмпирическая функция распределения при неограниченном увеличении объема выборки сходится к функции распределения наблюдаемого признака по вероятности равномерно по х, то есть .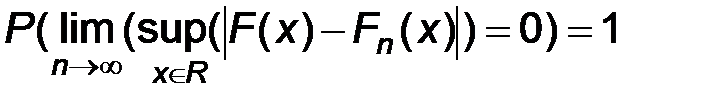

Определение. Числовые характеристики эмпирической СВ называются эмпирическими числовыми характеристиками.

Это означает, что определены эмпирическое математическое ожидание, эмпирическая дисперсия, эмпирическое среднее квадратическое отклонение. Условимся в обозначениях эмпирических числовых характеристик употреблять в качестве нижнего индекса букву «э». Таким образом, по определению:

, ,

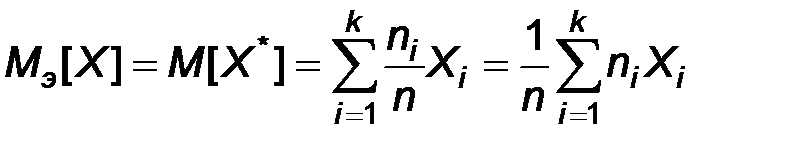
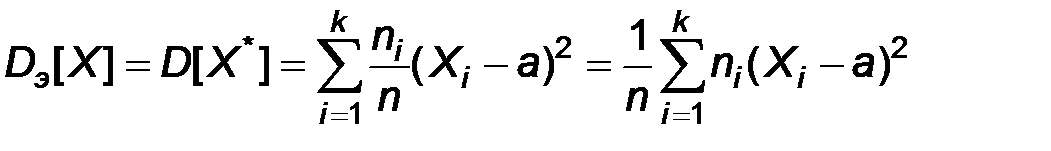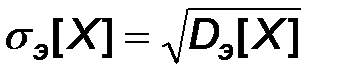при этом, как обычно, .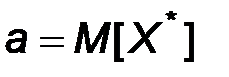

Теорема Гливенко-Кантелли наводит на мысль о том, что эмпирические числовые характеристики должны быть приближенно равны соответствующим числовым характеристикам наблюдаемого признака.

Понятие о точечном оценивании параметров.

Пусть Х – наблюдаемый признак с известным видом функции (плотности, закона) распределения. Будем предполагать, что функция распределения зависит от параметров: .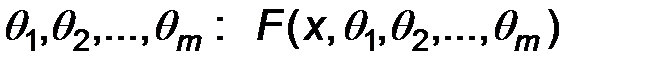

Назовем точечной оценкой параметра 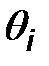всякую формулу, которая по результатам выборки позволяет расчитывать приближенное значение параметра: .

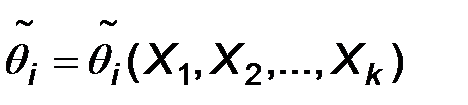Отметим, что точечную оценку, как и выборку, можно рассматривать с двух точек зрения: как расчетную формулу или как случайную величину.

Пример. Как известно, нормально распределенная СВ задается плотностью распределения

,

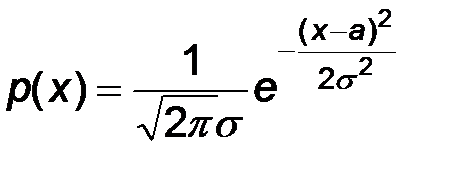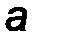зависящей от двух параметров . Поскольку при этом является математическим ожиданием, а - средним квдратическим отклонением, то учитывая теорему Гливенко-Кантелли, естественно предположить, что 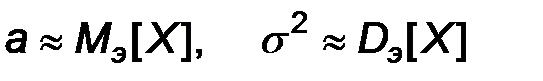. Эти соображения приводят к следующей паре точечных оценок

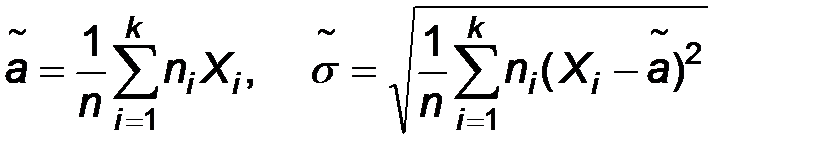
Замечание. Разумеется, для одного и того же параметра, как правило, существует много оценок. Например, в предыдущем примере в качестве оценки математического ожидания можно выбрать первое из производимых измерений наблюдаемого признака.

В связи с этим, среди оценок следует выбирать наилучшие. Для отбора используют следующие критерии:

1. Несмещенность. Точечная оценка параметра называется несмещенной, если математическое ожидание оценки совпадает с истинным значением этого параметра: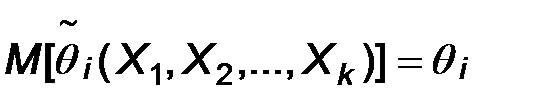

2. Состоятельность. Точечная оценка параметра называется состоятельной, если при неограниченном увеличении объема выборки СВ 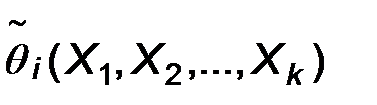сходится по вероятности к истинному значению этого параметра, т.е. если 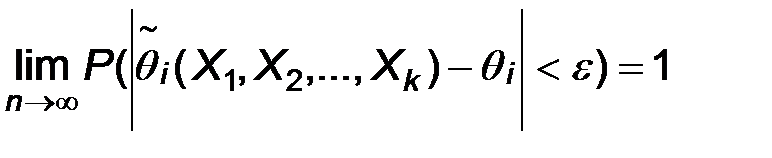каково бы ни было .

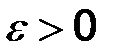3. Эффективность. Несмещенная точечная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок рассматриваемого параметра.

Замечание. При формулировке критериев, предъявляемых к точечным оценкам мы рассматривали последние как случайные величины.

Точечная оценка математического ожидания.

Пусть задан вариационный ряд частот наблюдаемого признака Х. Назовем выборочным средним и будем обозначать среднее арифметическое значений, наблюденных в выборке: 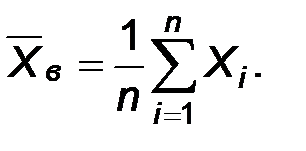Учитывая повторяющиеся значения, последнее выражение можно преобразовать следующим образом:

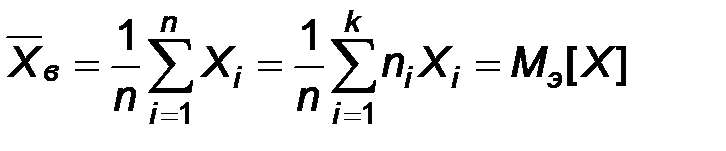
Таким образом, выборочное среднее является эмпирическим математическим ожиданием и, поэтому, во-первых, обладает всеми свойствами математического ожидания, во-вторых, является точечной оценкой математического ожидания наблюдаемого признака. Более того, эта оценка яляется наилучшей в силу следующей теоремы.

Теорема. Выборочное среднее есть несмещенная, состоятельная, эффективная оценка математического ожидания.

Доказательство. Учитывая, что результаты наблюдений можно рассматривать как случайные величины, имеющие такое же распределение, как и наблюдаемый признак, получаем

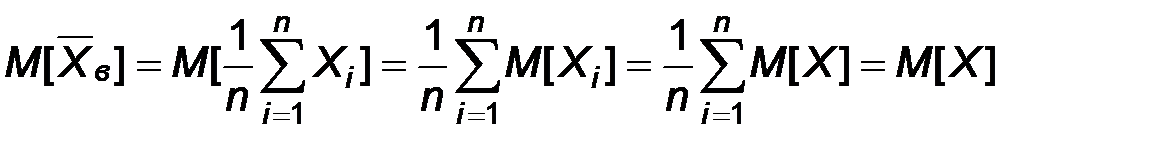
Таким образом, несмещенность доказана.

С другой стороны, в силу теоремы закона больших чисел

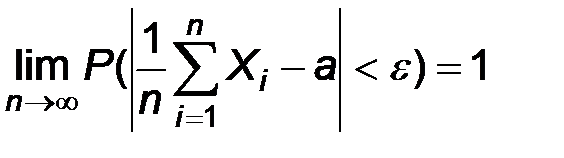
каково бы ни было e>0. Последнее означает состоятельность выборочного среднего как точечной оценки математического ожидания.

Доказательство эффективности проводится по следующей схеме. Сначала показывают, что минимумом для дисперсий среди всех несмещенных оценок математического ожидания является величина 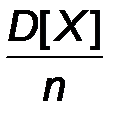, а затем замечают, что .

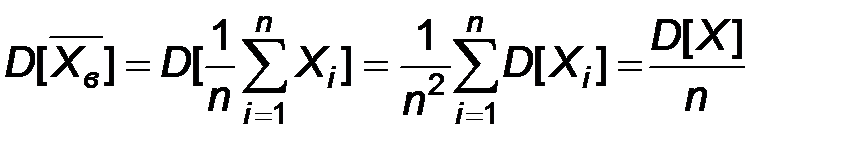Теорема доказана.

Точечные оценки дисперсии.

По аналогии с математическим ожиданием в качестве точечной оценки дисперсии будем считать точечной оценкой дисперсии среднюю выборочную дисперсию:

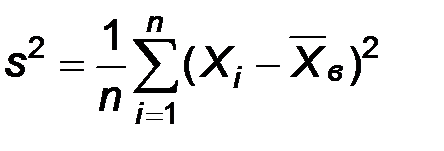
Теорема. Оценка 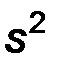является смещенной, а именно 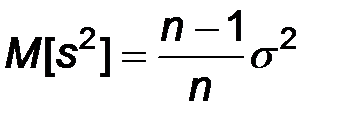, где 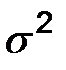- дисперсия наблюдаемого признака.

Доказательство. Пусть a –математическое ожидание наблюдаемого признака, тогда

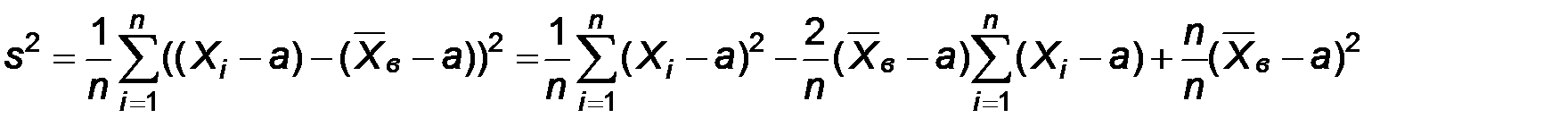Принимая во внимание, что 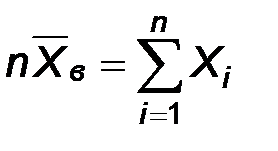, получим

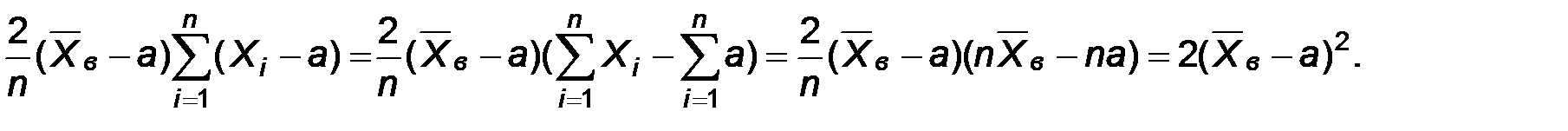Тогда

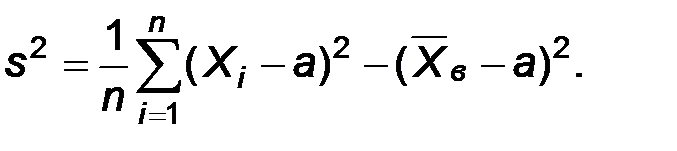
Следовательно,

.

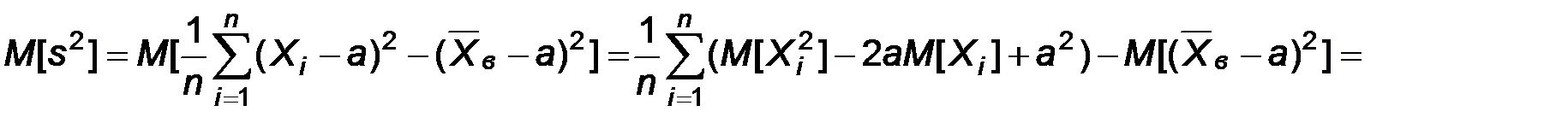
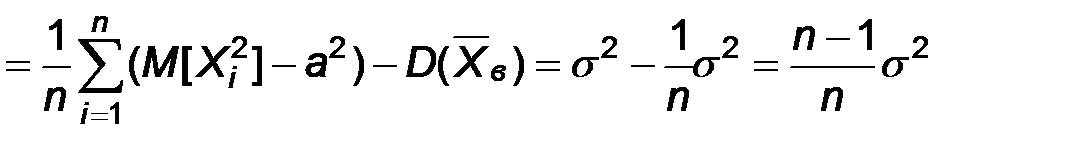Теорема доказана.

Следствие. Несмещенной оценкой дисперсии является

.

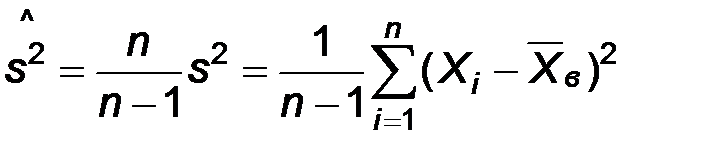Эту оценку называют исправленной выборочной дисперсией.

Дробь 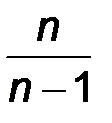называют поправкой Бесселя. Очевидно, эта поправка стремится к 1 при увеличении объема выборки и при п >50 разница между исправленной дисперсией и дисперсией выборки практически неощутима. Пользуясь законом больших чисел можно показать, что обе рассмотренные оценки являются состоятельными. Однако, исправленная выборочная дисперсия не является эффективной оценкой дисперсии. Можно показать, что несмещенной, состоятельной, эффективной оценкой дисперсии является следующая оценка 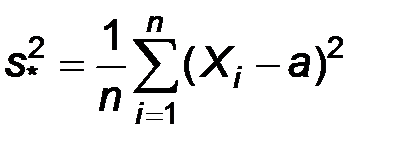. Однако, эта оценка практически неприменима, ибо для ее построения необходимо знание точного значения математического ожидания.

Методы построения точечных оценок.

1. Метод максимального правдоподобия.

Пусть 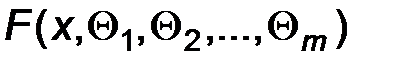- функция распределения, плотность распределения или вероятность того, что случайная величина Х примет значение х.

Ясно, что первые две функции используют для непрерывных наблюдаемых признаков, а первую и третью – для дискретных наблюдаемых признаков.

Назовем функцией правдоподобия следующую функцию

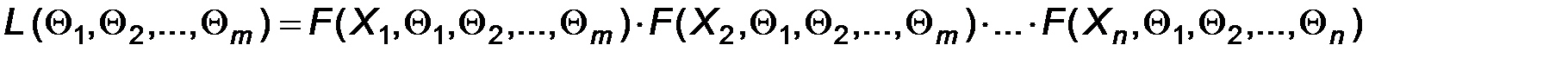где 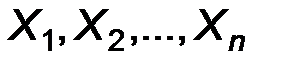- выборка объема и значений Х.

Теорема. Пусть 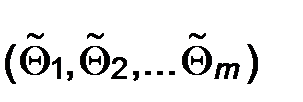- точка максимума функции L, тогда 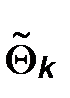есть состоятельная оценка параметра .

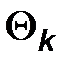Эту теорему мы приводим без доказательства.

Из приведенной теоремы вытекает следующая схема поиска точечных оценок:

1. Составить функцию максимального правдоподобия L.

2. Исследовать функцию L на максимум, для чего составить и решить систему уравнений

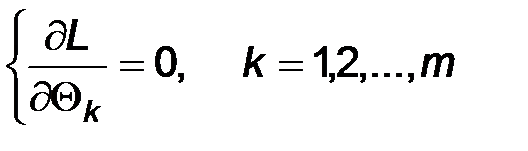
После чего проверить, что найденные решения этой системы доставляют максимум функции L.

3. Выписать полученные точечные оценки.

Замечание. Если f(x) возрастающая функция, то функция L и f(L) имеют максимумы в одних и тех же точках. Поэтому в пункте 2 схемы можно вместо функции L использовать функцию f(L), что иногда проще при удачном выборе функции f(x).

Пример. Построить точечные оценки параметров 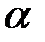и 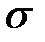нормально распределенного признака по результатам выборки. .

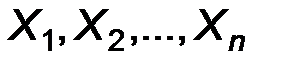Поскольку плотность распределения в рассматриваемом случае имеет вид: , то функция правдоподобия имеет вид

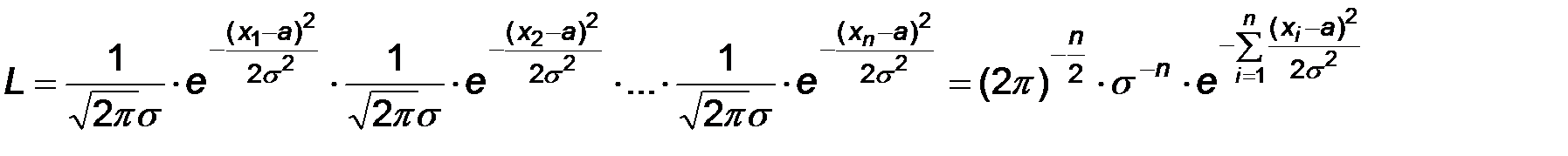Будем рассматривать вместо функции L, следую замечанию, функцию lnL:

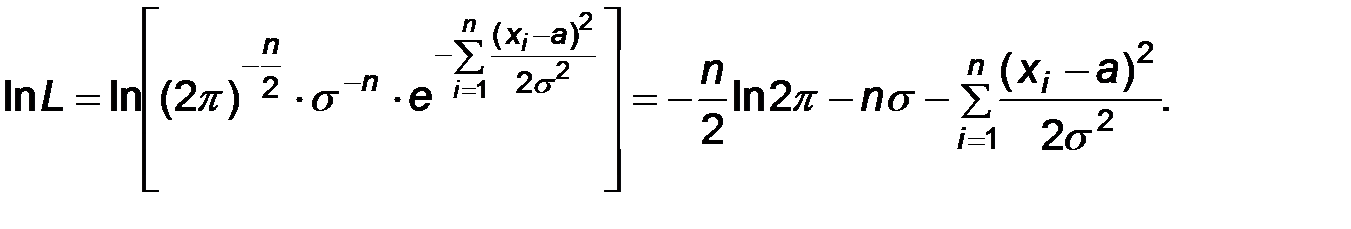
Тогда

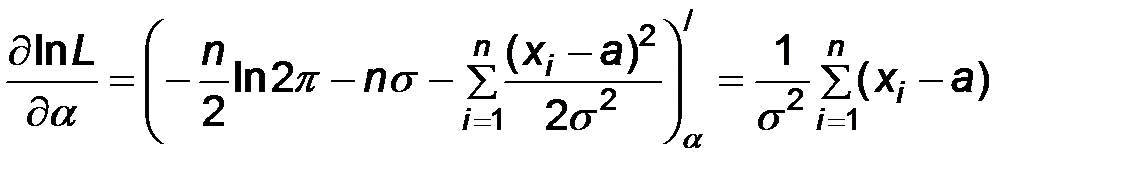
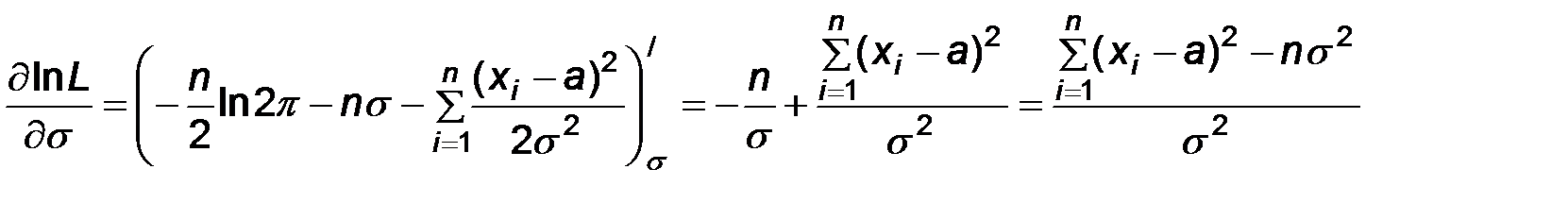
Приравнивая к нулю частные производные, получаем

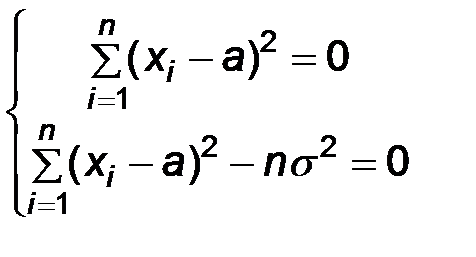
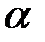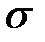Решая эту систему относительно и , получаем:

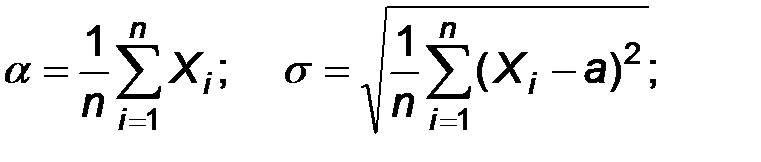
Можно проверить, что полученные значения действительно доставляют максимум функции lnL.

Следствие. В рассмотренном примере получены следующие оценки математического ожидания и дисперсии

, .

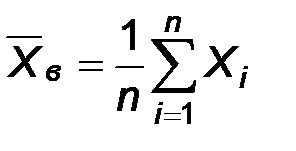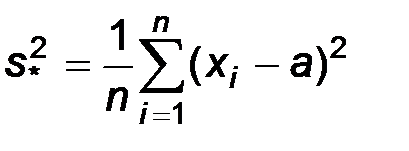2. Метод моментов.

Пусть 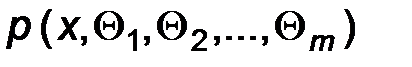- плотность распределения признака Х, а 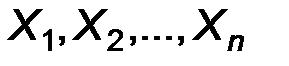- выборка объема n.

Представим эту выборку в виде вариационного ряда относительных частот:

X*			…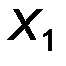
			…

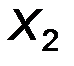
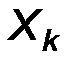
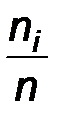
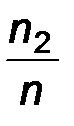
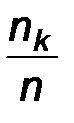
Этот ряд, как отмечалось выше, определяет эмпирическую случайную величину Х*, которая является некоторым приближением наблюдаемого признака Х. Последнее означает, что моменты произвольных порядков величин Х и Х * должны быть приблизительно равны:

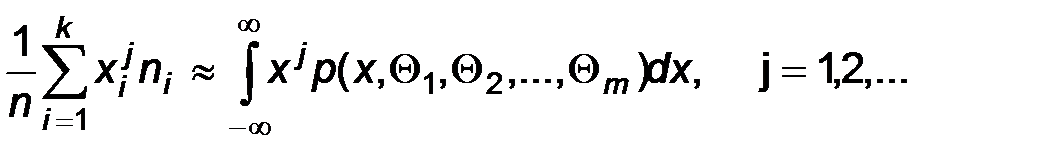
Выбирая m уравнений, получаем систему, решения которой дают оценки параметров .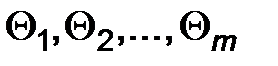

Пример. Методом моментов построить оценку параметра 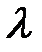для распределения Пуассона.

Плотность распределения имеет вид

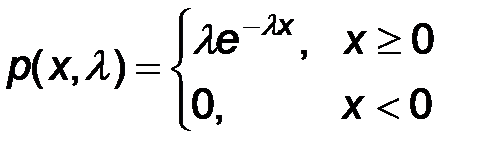
где: 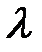>0/.

Найдем моменты первого порядка случайных величин Х и Х*:

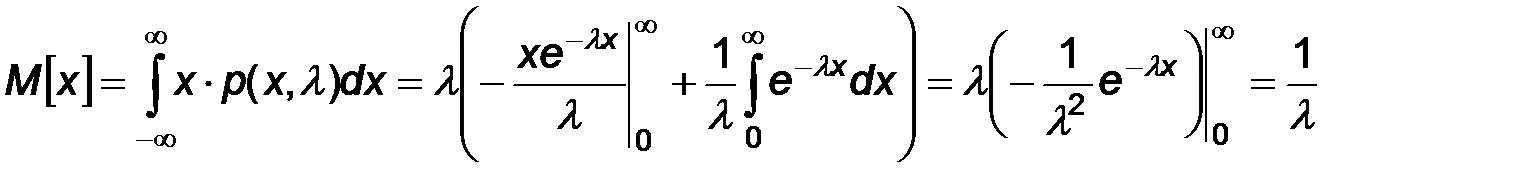
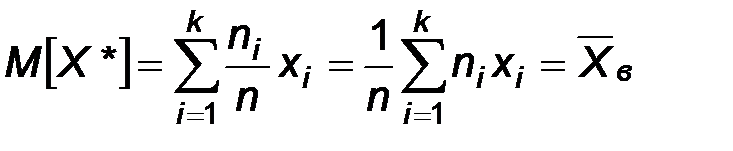
Следовательно, 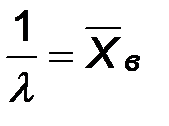и .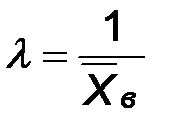

Доверительное оценивание параметров.

Дата добавления: 2014-12-10