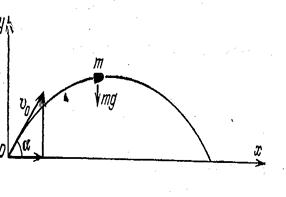
Тело, брошено под углом к горизонту

Как и в случае горизонтально брошенного тела, тело движется, в результате комбинации двух движений: равномерного прямолинейного движения под углом к горизонту и свободного падения в вертикальном направлении (под действием только силы тяжести – без реакции опоры).

В двумерной постановке тело, брошенное под углом к горизонту, рассматривается как материальная точка, движущаяся под действием лишь одной силы - постоянной силы его веса Р, направленной вертикально вниз. Начало координат – в точке приложения силы, обеспечившей начальную скорость полета.

Тело массы m, брошенное под углом к горизонту, движется под действием постоянной силы веса Р = F _т, направленной вертикально вниз Р = mg.

Уравнения движения можно представить как в векторной, так и в координатной форме.

Для произвольной точки М (х, у) траектории тела:

m v = Р t + m v ₀, или v = gt + v ₀.

Проецируя векторные соотношения на оси координат, получим уравнения движения в координатной форме.

m dv _x / dt = 0, v _x = dx / dt,

m dv _y / dt = - mg, v _y = dy / dt

Необходимо найти зависимости x (t), y (t), v _x(t), v _y(t) из решения полученной системы дифференциальных уравнений при начальных условиях:

x (0) = x ₀, y (0) = y ₀, v _x (0) = v ₀ cos Θ ₀, v _y (0) = v ₀ sin Θ ₀.

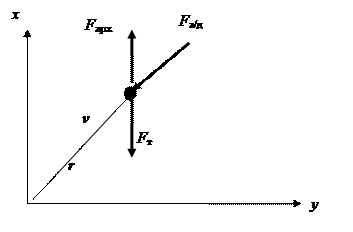
Сопротивление воздуха

Cила сопротивления воздуха F _а/д (полная аэродинамическая сила) направлена противоположно вектору скорости тела прямо пропорциональна величине скоростного потока q и характерной площади тела S:

F _а/д = - C r qS, q = ρv ²/2,

где C r - коэффициент сопротивления, зависящий от свойств среды и тела, скорости потока, ρ [кг/м³] – плотность воздуха, зависит от высоты.

Коэффициент сопротивления определяется опытным путем, и для приближенных расчетов для тела в форме шара может быть принят независимым от скорости потока и равным 0,25 (плюс – минус 0,05 – в зависимости от скорости).

Тогда система уравнений запишется в виде:

dv _x / dt = C r qS cos Θ / m, v _x = dx / dt,

dv _y / dt = C r qS sin Θ / m - g, v _y = dy / dt

ρ = ρ (y), α = arctg v _x / v _y, q = ρv ²/2

при начальных условиях:

x (0) = x ₀, y (0) = y ₀,

v _x (0) = v ₀ cos Θ ₀, v _y (0) = v ₀ sin Θ ₀.

Зависимость ρ = ρ (y) может быть задана в табличном или в аналитическом виде.

Задача не имеет аналитического решения и решается численным интегрированием. Определяется влияние шага интегрирования на точность решения задачи.

Изменение с высотой величины ускорения силы тяжести Земли

Ускорение свободного падения одинаково для всех тел и, также как и вес, зависит от географической широты и высоты над уровнем моря.

Стандартное (нормальное) значение ускорения свободного падения на уровне моря составляет g0 = 9,81 м/сек². Для определения ускорения при удалении от поверхности Земли на высоту h используется формула g = g₀[R₀/(R₀ + h)]², R₀ = 6370 км - радиус Земли. На географических полюсах (φ = 900) Fц = 0 и вес тела равен силе притяжения его к Земле. Вследствие того, что центростремительная сила зависит от широты, вес тела максимален на полюсах и минимален на экваторе, различие не превышает 0,55%.

Величина выталкивающей силы (закон Архимеда)

На тело действует выталкивающая сила воды в соответствии с законом Архимеда.

По закону Архимеда выталкивающая сила равна F _арх = g (y) Vρ ₀(y). Здесь Vρ ₀(y) – масса вытесненного воздуха, V – объем тела.

Величины присоединенной массы

Присоединенная масса может быть определена по формуле: m = 0,5 Vρ ₀.

Изменения плотности атмосферы с высотой

Гипотеза о постоянстве плотности атмосферы (ρ ₀ = 1,225 кг/м³) с высотой полета изменяется ρ = ρ (h), где h – высота над уровнем моря [м]: ρ = ρ ₀^{- 0, 00014 h}.

Кривизны Земли

Для учета кривизны Земли необходимо строить новую математическую модель - начало системы координат помещается в центр Земли. В этом случае сила притяжения направлена в начало координат (а не перпендикулярно оси координат), и тип кривой полета становится другим (эллипс, а не парабола).

Дата добавления: 2014-11-29