Истинность высказываний с кванторами

Выясним теперь, как устанавливают значения истинности высказываний, содержащих кванторы.

Рассмотрим сначала высказывание с квантором общности, т.е. высказывание вида (" х Î Х) А(х). В нем утверждается, что для любого х из множества Х истинно А(х), поэтому, чтобы убедится в истинности этого высказывания, надо показать, что множество истинности Т_А высказывательной формы А(х) совпадает с множеством Х (Т_А = Х). Чтобы убедится в ложности высказывания (" х Î Х) А(х), достаточно показать, что Т_А ¹ Х, т.е. показать, что существует такое значение х Î Х, при котором высказывательная форма обращается в ложное высказывание.

Задача 2. Установить, истинны или ложны следующие высказывания:

а) Для каждого х из множества {0, 1, 4} значение выражения (4–х): (2х+ 1) есть число целое.

б) Произведение двух любых последовательных натуральных чисел кратно 2.

в) Всякое натуральное число делится на 5.

Решение. а) Если мы хотим убедиться в истинности данного высказывания, то надо показать, что при подстановке каждого числа из множества{0, 1, 4}в выражение (4 – х): (2х +1) получается целое число. Имеем:

если х = 0, то (4-0): (2×0+1)=4;

если х = 1, то (4-1): (2×1+1)=1;

если х = 4, то (4-4): (2×4+1)=0.

Действительно, значение выражения (4 – х): (2х +1) при всех заданных значениях х есть число целое. Установили мы это путем перебора всех возможных случаев.

б) Воспользуемся результатом задачи 1 (случай б) и представим данное высказывание в таком виде: (" хÎ N) х (х+1) 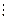2.

Мы не знаем, истинно оно или ложно, поэтому рассмотрим несколько случаев. Если х =1, то произведение 1×2 кратно 2, так как на 2 делится второй множитель. Если х =2, то произведение 2 × 3 тоже кратно 2, так как на 2 делится первый множитель. Если х = 7, то и в этом случае 7 × 8 кратно 2, поскольку второй множитель 8 делится на 2. Исходя из рассмотренных случаев, можно предположить, что данное высказывание истинное, но убедится в этом путем перебора (как в первом предложении) нельзя, поскольку невозможно перебрать все натуральные значения х. Будем рассуждать. Из двух последовательных натуральных чисел одно обязательно четное. Но если в произведении один из множителей делится на 2, то, как известно, и все произведение делится на 2. Следовательно, при любом натуральном х произведение х (х+1) делится на 2.

в) Высказывание «всякое натуральное число делится на 5» – ложное. Убедится в этом можно, назвав натуральное число, которое не делится на 5, например число 12.

В математике говорят, что в ложности данного высказывания мы убедились, приведя контрпример.

Замечание. Истинность высказывания с квантором общности устанавливается путем доказательства. Показать ложность таких высказываний можно, приведя контрпример.

Выясним, как устанавливается значение истинности высказываний, содержащих квантор существования. В высказывании ($ х Î Х) А(х) утверждается, что в множестве Х есть такой элемент х, который обладает свойством А. Поэтому оно будет истинно, если множество истинности высказывательной формы А(х) не пусто (Т_А ¹Æ). Для того чтобы показать это, достаточно найти такое значение переменной х, при котором высказывательная форма А(х) обращается в истинное высказывание, т.е. привести пример.

Высказывание ($ х Î Х) А(х) ложно в том случае, когда Т_А = Æ. Убедится в этом можно лишь путем доказательства.

Задача 3. Установить, истинны или ложны следующие высказывания:

а) Среди треугольников есть прямоугольные.

б) Некоторые прямоугольные треугольники являются равносторонними.

Решение. а) Данное высказывание содержит квантор существования, который выражен словом «есть». Чтобы убедится в истинности такого высказывания, достаточно привести пример. В данном случае прямоугольный треугольник можно начертить.

б) В этом случае квантор существования выражен словом «некоторые». Если считать данное высказывание истинным, то надо привести пример, т.е. попытаться начертить треугольник, который был бы одновременно прямоугольным и равносторонним. Из того, что это не удается начертить, еще не следует вывод о ложности данного высказывания. В этом надо убедится путем доказательства.

Действительно, если треугольник прямоугольный, то в нем один угол равен 90°, а в равностороннем все углы 60°. Следовательно, ни один прямоугольный треугольник не может быть равносторонним. Поэтому данное высказывание ложное.

Замечание. Истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Чтобы убедится в ложности такого высказывания, необходимо провести доказательство.

Заметим, что убедится в ложности высказывания – это значит опровергнуть его.

Дата добавления: 2014-12-16