И метода определения момента инерции

Основной закон динамики для вращательного движения

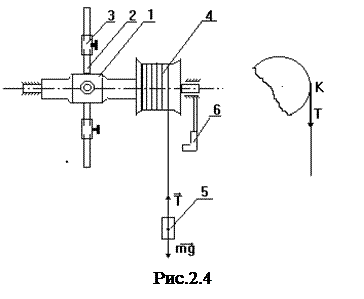
В случае, если момент инерции тела в процессе вращения остается постоянным, “Основной закон...” читается так: момент силы (или результирующий момент сил, если их несколько), действующий на тело относительно оси вращения, равен произведению момента инерции тела относительно этой оси на угловое ускорение, с которым вращается тело:

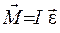. (2.11)

Описание установки

Маятник Обербека представляет собой крестовину, состоящую из втулки 1, четырех спиц 2, укрепленных на одном из концов втулки. На спицах размещены грузы 3. Последние могут перемещаться вдоль спиц и закрепляться на них с помощью винтов. Другой конец втулки выполнен в виде шкива 4, на который наматывается нить-шнур. К свободному концу шнура привязан груз 5. Под влиянием этого груза маятник приходит в ускоренное вращательное движение вокруг непо­д­вижной оси. Трение между втулкой маятника и осью практически сведено к нулю установленными на ось подшипниками. Для установки груза 5 на определенной высоте предусмотрен указатель 6. Исходным уравнением для определения момента инер­ции I маятника является уравнение (2.11), из которого следует, что

, (2.12)

где M - вращающий момент, в данном случае - момент силы Т натяжения шнура, приложенной в точке k (рис.2.4); 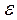- угловое ускорение маятника. Мо­мент силы берется отно­сительно оси вращения, а потому

М = T R, (2.13)

где R - радиус шкива.

Сила T может быть найдена из второго закона Ньютона. записанного для груза 5:

ma = mg - T,

где m - масса груза 5; а - ускорение, с которым он опускается, откуда

Т = m (g - а). (2.14)

Таким образом, подставляя (2.14) в (2.13), получим

М = m(g - a) R. (2.15)

Угловое ускорение e связано с тангенциальным ускорением точек на ободе колеса следующим соотношением:

.

В свою очередь, совпадает с ускорением а, с которым опускается груз 5. Следовательно,

. (2.16)

Ускорение а можно вычислить, если измерить время t опускания груза 5 на определенную высоту h. Действительно

,

а потому

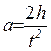. (2.17)

Подставляя (2.17) в (2.16) и (2.15), а затем в (2.12), получим

, (2.18)

где d = 2 R - диаметр шкива.

Заметим, однако, что второе слагаемое в выражении (2.18) оказывается на практике значительно меньше первого, а потому момент инерции маятника можно вычислить как

. (2.19)

Формула (2.19) - рабочая формула для определения I из законов динамики. С другой стороны, как уже отмечалось, момент инерции тела - величина аддитивная. Следовательно, момент инерции маятника Обербека относительно оси вращения можно представить в виде

I = I _в + I _ш + 2 I _сп + 4I _гр, (2.20)

где: I _в - момент инерции втулки; I _ш - момент инерции шкива; I _сп- момент инерции спицы; I _гр - момент инерции одного груза 3. (Разумеется, все эти моменты инерции в данном случае берутся тоже относительно оси вращения.)

Так как ,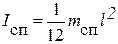

где l и m _пс- общая длина (рис.2.5) и масса двух спиц, а для случая, когда грузы 3 находятся на концах спиц,

I _гр = m _гр l ₁²

(груз - материальная точка), где l ₁- расстояние от центра масс груза до оси, а m _гр - масса груза 3, то

I = (I _в + I _ш ) + 1/6 × m _пс l² + 4 m _гр l ₁². (2.21)

Порядок выполнения работы

1. Внесите в таблицу данные о массе груза 5 и ускорении свободного падения для широты г. Пермь (написаны на приборе).

2.Установите грузы 4 на концы спиц, причем так, чтобы маятник находился в безразличном равновесии.

3. Наматывая нить на шкив, установите груз 5 так, чтобы основание груза совпало с указателем 6 (см. рис.2.4), (следите за тем, чтобы витки нити на шкив наматывались в один слой, а нить намоталась бы с внешней стороны маятника). В этом положении маятник придерживайте рукой за одну из спиц.

4. Измерьте время t ₁падения груза 5 с установленной высоты до пола. Для чего отпустите маятник без толчка, включив одновременно секундомер. Опыт повторите не менее 7 раз. Результаты занесите в таблицу.

5. Передвиньте грузы 3 примерно на середину спиц и установите их так, чтобы маятник находился в безразличном равновесии.

По п. 4 измерьте время t ₂ движения груза в этом случае. Результаты запишите в таблицу.

6. Измерьте диаметр шкива d и высоту падения груза h, оцените ошибкиD d иD h в измерении этих величин. Данные занесите в таблицу.

7. Вычислите < 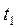> и < > и по формуле

< I > = ,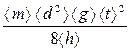

вычислите среднее значение моментов инерции и 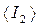(для того и другого расположения грузов 3).

8. Определите абсолютную и относительную погрешности в определении момента инерции (только для или только для , так как погрешности будут приблизительно одинаковыми).

Для чего:

Номер опыта		t2	t1i - < t1>	(t1i - <t1>)^2	Другие данные
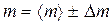. . .					g = … ± … d =… ± … h =… ± … a = D t1 =
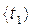	=	=	S (t1i - < t1>)^2 =

а) задайтесь надежностью a (от 0,90 до 0,97), выберите коэффициент Стьюдента , оцените D t _пр для секундомера;

б) вычислите абсолютную погрешность в измерении времени:

;

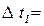
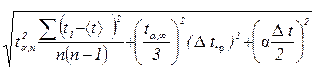в) вычислите относительную погрешность в определении I (например, I ):

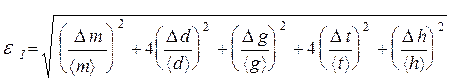
г) вычислите абсолютную погрешность:

;

д) результаты запишите в виде

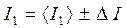, при %,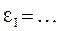

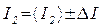. a =...

9. Сравнивая 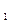I и I 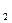, сделайте вывод (касающийся связи величины момента инерции и расположения грузов 3).

10. Измерьте l и l 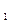(лучше 2 l 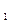) (см. рис.2.5) и по формуле (2.20) вычислите момент инерции как аддитивную величину I ₁^ад (m _иc, m _гр и (I _в + I _ш ) должны быть даны). Значения всех этих величин внесите в тетрадь.

11. Найдите расхождение в процентах между значениями I ₁ и I ₁^ад, полученными из опыта и вычисленными по формуле (2.21).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется моментом инерции материальной точки относительно оси, моментом инерции твердого тела относительно оси?

В каких единицах измеряется момент инерции?

2. В чем состоит теорема Штейнера? Приведите пример ее использования.

3. Что называется моментом силы относительно оси? В каких единицах он измеряется?

4. Что такое плечо силы?

5. Что называется моментом импульса материальной точки относительно оси вращения, моментом импульса твердого тела относительно оси вращения? В каких единицах измеряется момент импульса?

6. Как связаны между собой момент импульса и момент инерции тела, вычисленные относительно оси вращения?

7. Маятник Обербека: устройство и теория метода определения его инерции.

8. Порядок выполнения работы. Выводы.

ЛАБОРАТОРНАЯ РАБОТА № 3

Дата добавления: 2014-12-16