Определение открытой системы

Система является замкнутой в том и только в том случае, если поток энергии на входе и выходе системы равен нулю.

Однако такая ситуация является лишь частным случаем. В общем случае поток энергии на входе и выходе системы не равен нулю. Замкнутые системы являются частным случаем открытых систем.

Система является открытой тогда и только тогда, когда она обменивается потоками энергии с окружающей ее средой.

Полный поток. Активный поток. Пассивный поток

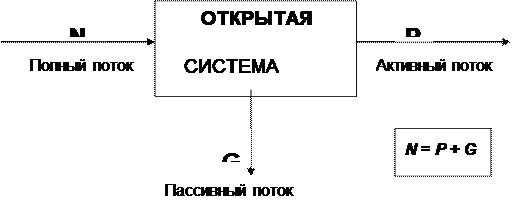Принципиальной особенностью открытых систем является то, что полный поток N на входе в систему равен сумме активного P и пассивного G (или потерь) потоков на выходе из системы (рис. 3.7):

18. Полная мощность. Полезная мощность и мощность потерь

Полная мощность системы — это полный поток энергии на входе в систему N.

Полезная мощность системы — это активный поток энергии (поток свободной энергии) на выходе системы P.

Мощность потерь системы — это пассивный поток энергии или поток связной энергии G.

19. Уравнение полной мощности

В соответствии с данными определениями полная мощность системы равна сумме полезной мощности и мощности потерь:

N = P + G 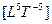. (3.18)

20. Связь мощности, энергии и энтропии

Мощность и энергия различаются на величину производной по времени. Имеем:

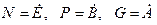. (3.19)

Из этих определений видно, что поток связной энергии 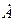есть мощность потерь G. Следовательно, связная энергия — это интеграл от мощности потерь, то есть «отработанная» энергия, или теплота. Однако такое понимание теплоты расходится с существующим представлением теплоты как лучистой энергии, которая рассеивается звездами в мировое пространство. Мы считаем, что хотя лучистую энергию и принято называть теплотой — тем не менее это утверждение является некорректным. Это электромагнитное излучение превращается в теплоту тогда и только тогда, когда прошел эффект поглощения этого электромагнитного излучения веществом (в газовой, жидкой или твердой фазе). Теплота нагретых тел, в какой бы фазе эти тела не находились, опять излучаются в виде электромагнитного потока в соответствии с законом Стефана—Больцмана, пропорционально четвертой степени абсолютной температуры. Мы специально остановились на этом вопросе потому, что это имеет принципиальное значение при выяснении того, что представляет энтропия. Энтропия и есть накопленный поток связной или «отработанной» энергии (теплоты) или точнее интеграл от мощности потерь, отнесенный к единице объема.

21. Различные формы энергии и мощности

Все возможные виды энергии: механическая, тепловая, магнитная, электрическая и др. являются ФОРМОЙ ЭНЕРГИИ и имеют единую пространственно-временную размерность .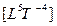

Также и мощность может быть представлена в различных формах. Например, механическая форма мощности имеет выражение:

,

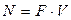где F — сила 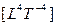, а V — скорость .

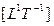Электрическая форма: 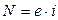, где e — напряжение 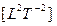, а 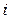— сила тока 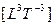; волновая форма мощности: 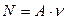, где А — амплитуда изменения свободной энергии 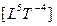, а 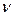— частота рабочих циклов .

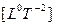Однако, полная мощность N произвольной системы равна сумме активной (полезной) Р и пассивной (мощность потерь) G частей, каждая из которых имеет размерность .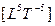

22. Закон сохранения мощности

В общем виде закон сохранения мощности записывается как инвариантность величины мощности:

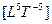= const. (3.20)

Из уравнения полной мощности N = P + G следует, что полезная мощность и мощность потерь проективно инверсны и поэтому любое изменение свободной энергии 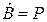компенсируются изменением мощности потерь 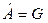под контролем полной мощности .

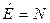Полученный вывод дает основание представить ЗАКОН СОХРАНЕНИЯ МОЩНОСТИ в виде скалярного уравнения:

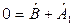, где 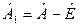. (3.21)

Содержательный смысл уравнения прозрачен: изменение свободной энергии компенсируется разностью между потерями и поступлениями энергии в систему.

Несложно показать, что существует связь мощности с другими потоками, например, действием 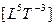, моментом инерции 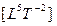и другими.

Связь мощности с действием:

, , .

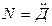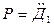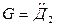Связь мощности с моментом инерции:

, , .

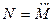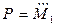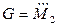Нетрудно установить связи мощности и с другими величинами. Но не это главное. Суть вопроса в том, что все потоки имеют единую структуру законов сохранения. В силу этого мы можем представить закон сохранения мощности как иерархию уравнений:

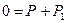, где 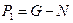, 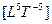(3.22)

или

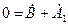, где 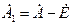, , 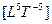(3.23)

или

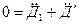, где 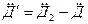, , 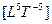(3.24)

или

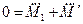, где 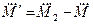, 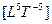. (3.25)

Содержательный смысл этих уравнений сохраняется на всех уровнях.

Изменение активного потока компенсируется разностью между потерями и поступлениями в систему.

Таким образом механизм открытой системы снимает ограничения замкнутости, и тем самым предоставляет возможность дальнейшего движения системы.

Однако этот механизм не показывает возможных направлений движения — эволюции систем. Поэтому он должен быть дополнен механизмами эволюционирующих и неэволюционирующих систем или неравновесных и равновесных.

23. Равновесные и неравновесные системы

Дата добавления: 2014-11-29