История российского государства и права

Задача про призначення

Транспортна задача.

Перевезення вантажів – це обов’язкова компонента нашого повсякденного життя. Тому задача про вартість такого перевезення та її оптимізацію є класичною. В процесі перевезення є дві сторони – постачальники транспортних послуг та одержувачі вантажів (покупці). Класична постановка транспортної задачі є закритою, це означає, що передбачається баланс між обсягами відправленого вантажу від постачальників та одержаного вантажу покупцями за критерієм мінімуму суми транспортних витрат. Якщо ж задача відкрита, то її приводять до закритого типу шляхом введення фіктивного постачальника або покупця.

У задачі відомі можливості кожного постачальника (потужність постачальника) і можливості кожного покупця (потужність покупця), тарифи на перевезення одиниці вантажу від кожного постачальника до кожного покупця.

У якості обмежень виступають умови по обов’язковому задовільненою потреб покупців та використанню всіх ресурсів постачальників.

Таблиця 5.4 Узагальнені дані транспортної задачі для чотирьох постачальників і чотирьох покупців

Постачальник (Bi)	Потуж-ність постача-льника	Потужність покупця (Aj)
Покупець 1	Покупець 2	Покупець 3	Покупець 4
А1	А2	А3	А4
Постачальник 1	В1	С11	С12	С13	С14
Постачальник 2	В2	С21	С22	С23	С24
Постачальник 3	В3	С31	С32	С33	С34
Постачальник 4	В4	С41	С42	С43	С44

Математична модель задачі.

Змінні – кількість одиниць вантажу, який перевозиться від і-го постачальника до j-го покупця – х_ij.

Цільова функція: ,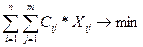

де n – кількість постачальників,

m – кількість покупців,

Cij – тарифи на перевезення одиниці вантажу від і-го постачальника до j -го покупця,

Обмеження:

для постачальників ,

для покупців .

Приклад 5.2. Вантаж перевозиться від чотирьох постачальників чотирьом покупцям. Всі вхідні дані зведені у таб. 5.5. На перехресті рядків і стовпців вказані тарифи на перевезення. Необхідно скласти оптимальний план перевезень за критерієм мінімуму витрат.

Таблиця 5.5 Дані для приклада 5.2

Постачальник	Потуж-ність постача-льника	Потужність покупця	Разом
Покупець 1	Покупець 2	Покупець 3	Покупець 4
Постачальник 1
Постачальник 2
Постачальник 3
Постачальник 4
Разом

Виконання.

1. Перевірка задачі на закритість – підрахувати суми потужностей покупців та постачальників (Разом по стовпцю і Разом по рядку). Обсяг вантажу у постачальників менше, ніж потрібно покупцям. З таб. 5.5 випливає, що сумарний обсяг вантажу у постачальників на 20 од. Менше, ніж потрібно покупцям.

Розв’язання такого типу задачі можна виконати двома способами:

Варіант 1. Привести задачу до класичного варіанту шляхом введення в таблицю Фіктивного постачальника з обсягом вантажу в 20 од. і з нульовими транспортними тарифами. Тоді будуть збалансовані обсяги і задача буде розв’язана класичним методом.

Варіант 2. Не вводити фіктивного постачальника, але тоді в системі обмежень змінити умови постачання покупцю: знак строгої рівності замінити на нестрогу рівність <=.

Розглянемо рішення задачі послідовно в двох варіантах.

2. Додамо в таблицю 5.5 рядок з фіктивним постачальником з обсягом постачання 20 од. та нульовими транспортними витратами (таб. 5.6).

3. Для застосування метода Поиск решения Excel необхідно підготувати чарунки так, як на рис. 5.6. Для скорочення запису цільової функції задачі варто використати математичну функцію СУММПРОИЗВ: =СУММПРОИЗВ(C16:F20;C4:F8).

Таблиця 5.6 Модифіковані дані для приклада 3.16

	A	B	C	D	E	F	G
	Постачальник	Потуж-ність постача-льника	Потужність покупця	Ра-зом
	Покупець 1	Покупець 2	Покупець 3	Покупець 4
	Постачальник 1
	Постачальник 2
	Постачальник 3
	Постачальник 4
	Фіктивнийпостачальник
	Разом

Рисунок 5.6 - Підготовка даних до використання методу Поиск решения

4. Викликати вікно метода Поиск решения та заповнити його (рис. 5.7).

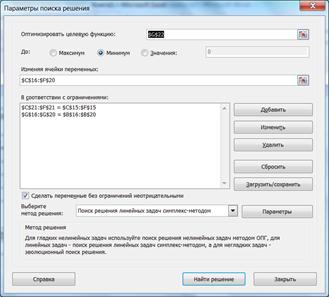
Рисунок 5.7 – Заповнення полів вікна Поиск решения при розв’язанні транспортної задачі

В результаті рішення був одержаний наступний розподіл вантажних потоків (таб. 5.7):

Таблиця 5.7 - Результати розрахунків транспортної задачі

	A	B	C	D	E	F	G
	Постачальник	Потуж-ність постача-льника	Потужність покупця	Ра-зом
	Покупець 1	Покупець 2	Покупець 3	Покупець 4
	Постачальник 1
	Постачальник 2
	Постачальник 3
	Постачальник 4
	Фіктивнийпостачальник
	Разом
					Цільова функція

З таб. 5.7 випливає, що Покупець 1 недоотримав вантаж в обсязі 20 од., тому, що введення фіктивного постачальника необхідно було для балансування обсягів поставки з обсягами споживання.

Тепер розглянемо другий варіант розв’язання відкритої транспортної задачі.

З вхідної таблиці 5.5 бачимо, що потужність постачальників на 20 од. менше потужності споживачів, тому у діалоговому вікні Поиск решения обмеження по покупцям не можуть йти зі знаком «=», їх потрібно вказувати зі знаком «<=»:

Тоді в результаті оптимізації одержимо рішення у таб 5.8.

Порівняння результатів розв’язання задачі 1 і 2 способами показують їх ідентичність. Суми транспортних витрат співпадають. Різниця тільки в тому, що при введені фіктивного постачальника будуть збалансовані загальні обсяги поставок і потреби покупців на реальну величину недопостачання вантажу - 20 одиниць.

Таблиця 5.8 Результати розв’язання транспортної задачі за варіантом 2

	A	B	C	D	E	F	G
	Постачаль-ник	Потуж-ність постача-льника	Потужність покупця	Разом
	Покупець1	Покупець 2	Покупець 3	Покупець 4
	Постачаль-ник 1
	Постачаль-ник 2
	Постачаль-ник 3
	Постачаль-ник 4
	Разом
					Цільова функція

У разі наявності у постачальників вантажу більше, ніж потребують покупці розв’язання задачі можна також виконувати будь-яким з приведених варіантів.

У разі використання покупцем послуг транспортних фірм мінімізація витрат покупця не буде задовольняти потреби постачальника послуг, якому потрібен максимум загальної вартості постачання. У цьому випадку має сенс використання консенсусного значення у діалоговому вікні Поиск решения для цільової чарунки (перемикач Значение).

Метою задачі про призначення є оптимальний розподіл робіт на підприємстві харчування. Класична трактовка мети розв’язання задачі міститься у наступному: необхідно скласти план виконання робіт так, щоб всі роботи були виконані, кожний робітник був завантажений тільки на одній роботі, а сумарна вартість виконаних робіт була мінімальною.

Таким чином, змінними у цій задачі виступають логічні параметри х_ij, які приймають значення 1, якщо I-a робота виконується j-м робітником, і 0, якщо вона не виконується цим робітником.

Вхідними даними будуть розцінки на роботи визначеного робітника (розрядність, кваліфікація, тощо) - c_ij.

Обмеження – один робітник на одну роботу. Це означає, що суми змінних по кожній роботі повинні дорівнювати 1 і суми змінних по кожному робітнику теж дорівнюють 1.

Цільова функція – сума добутку всіх змінних на розцінки робіт.

Приклад 5.3. П’ятеро робітників (бригада) на кухні можуть виконувати п’ять видів робіт. Вартість виконання і -м робітником j-ої роботи - С_іj (наведена в таблиці).

Працівники (і)	Види робіт (j) та почасова ставка відповідно кваліфікаційного розряду робітника (грн./час)
Підготовка продуктів	Закуски	Перші страви	Другі страви	Десерти
Астогина
Петров
Васильєва
Миронов
Романова

Виконання.

1. Спочатку треба підготувати робочий лист Excel до розв’язання задачі: виділити діапазон клітинок під змінні С20:G24 (рис. 5.8), ввести формули для обмежень у клітинки Н20:Н24 для працівників, у клітинки С25:G25 – на види робіт, у клітинки І20:І24 та С26:G26 ввести одиниці у якості правої сторони обмежень. У Н26 ввести формулу цільової функції.

2. Викликати надбудову Поиск Решения та ввести необхідні параметри (рис. 5.9). При цьому треба мати на увазі, змінні повинні бути цілочисельними, бо працювати пів людини не може.

	B	C	D	E	F	G	H	Константи для порівняння
	Працівники (і)	Види робіт (j) та почасова ставка відповідно кваліфікаційного розряду робітника (грн./час)	Обмеження на кількість виконуваних робіт 1 працівником
	Підготовка продуктів	Закуски	Перші страви	Другі страви	Десерти
	Астогина						=СУММ(C20:G20)
	Петров						=СУММ(C21:G21)
	Васильєва						=СУММ(C22:G22)
	Миронов						=СУММ(C23:G23)
	Романова						=СУММ(C24:G24)
	Обмеження на види робіт	=СУММ (C20:C24)	=СУММ (D20:D24)	=СУММ (E20:E24)	=СУММ (F20:F24)	=СУММ (G20:G24)	Цільова функція
							=СУММПРОИЗВ(C7:G11; C20:G24)

Рисунок 5.8 - Підготовка робочого листа до розв’язання задачі за прикладом 5.3

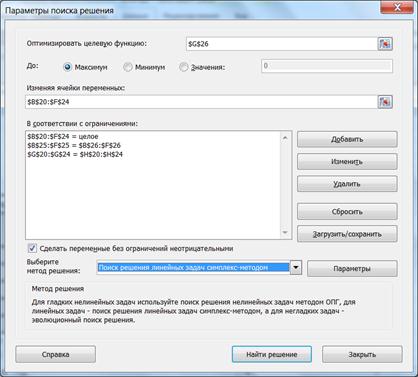
Рисунок 5.9 – Заповнення діалогового вікна Поиск решения для прикладу 5.3

Результати розв’язання задачі на мінімум вартості робіт мають наступний вигляд:

	B	C	D	E	F	G	H
	Працівники (і)	Види робіт (j) та почасова ставка відповідно кваліфікаційного розряду робітника (грн./час)	Обмеження на кількість виконуваних робіт 1 працівником
	Підготовка продуктів	Закус-ки	Перші страви	Другі страви	Десерти
	Астогина
	Петров
	Васильева
	Миронов
	Романова
	Обмеження на види робіт

Як бачимо, кожний робітник кухні буде зайнятий тільки на одній роботі. Тепер, виходячи з відпрацьованих годин у день і кількості виходів до роботи, одержимо денний заробіток кожного робітника за відпрацьовані робочі дні (таб. 5.9 А). У таб. 5.9 Б надані формули, по яких розраховані значення таблиці А.

Таким чином, мінімальна годинна вартість робіт всієї бригади складає 20,00 грн. При цьому, мінімальна вартість всіх виконаних робіт складе 3610 грн. /місяць. Але такий розподіл робіт не може задовольнити працівників через низьку бригадну суму зарплати. Тому спочатку розв’яжемо задачу з інтересів працівників (цільова функція максимум), а потім знайдемо консенсусне рішення для працівників та адміністрації.

При переключені в діалоговому вікні Поиск решения перемикача цільової функції на максимум знайдемо рішення й перерахуємо заробітну плату (таб. 5.10). Максимальна годинна вартість роботи всієї бригади складає 43,00 грн., а максимальна зарплата бригади складає 8570 грн./місяць, що набагато вище мінімального значення. Але підприємство харчування не має фінансових можливостей оплачувати бригаді таку суму. Необхідна договірна вартість робіт (консенсусна вартість), яка буде влаштовувати всіх. Консенсусна вартість повинна знаходитися у діапазоні між мінімумом та максимумом.

Допустимо, що в нашому випадку вона складає 35,00 грн./час. Тепер у діалоговому вікні встановлюваємо перемикач цільової функції на значение та вводимо 35, в результаті рішення одержимо перерозподіл робіт (таб. 5.11). Консенсусна годинна вартість робіт всієї бригади складає 35,00 грн., договірна зарплата бригади складає 6341,50 грн./місяць.

Як бачимо з вищенаведених таблиць в останньому стовпці вказана рекомендована оплата кожному робітнику відповідно цільової функції оптимізації. Але враховуючи бригадну роботу, робітники кухні можуть самостійно розподіляти загальну договірну суму бригади.

Таким чином, використовуючи такий інструментарій, як надбудову MS EXCEL Поиск решения можна моделювати розподіл не тільки будь - яких робіт, але й виконувати оптимізаційні розрахунки економічних показників з урахуванням обмежень матеріальних ресурсів

УЧЕБНИК

Дата добавления: 2014-12-16