Кратчайший путь между двумя пунктами

Метод присвоения меток

Методы определения кратчайших путей

Элементы теории графов

Методы и модели теории графов

		Рис. 1. Несвязный неориентированный граф

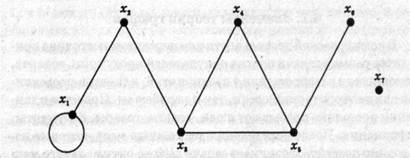
Для неориентированного графа на рис. 2 множество вер­шин X и ребер U можно записать так:

X = (х₁, …х₇)

U = ((х₁,х₁),(х₁,х₂)…(х₄, х₅), (х₅, х₆))

		Рис. 2 Ориентированный граф

Для ориентированного графа множества вершин и дуг запи­сываются следующим образом:

X = (х₁, …х₇)

U = ((х₁,х₂),(х₁,х₃), (х₃, х₂), (х₃, х₃), (х₃, х₄))

		Рис. Графы

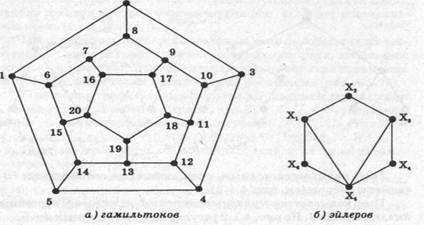
Самостоятельно. Для гамильтонова графа указать гамильтонову цепь и гамильтонов цикл.

Задача состоит в том, чтобы найти кратчайший путь на графе от какой-то выделенной вершины до любой другой вершины.

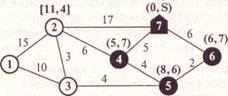
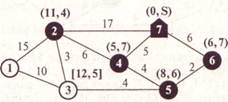
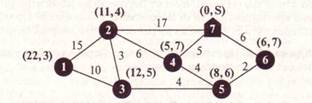
Пример. Узел 7 — склад, остальные узлы — строительные площадки компании. Показатели на дугах — расстояния в километрах.

Решение.

Как кратчайшим путем попасть из одной вершины графа в другую? В терминах управления цепями поставок: как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной.

Обозначения:

xi - исходный узел;

х_n - узел назначения;

d_ij - расстояние на сети между смежными узлами х_i и х_j.

Uj - кратчайшее расстояние от узла х_i до узла х_j. U₁=0.

Алгоритм нахождения кратчайшего пути состоит в последо­вательном нахождении значений Uj для каждого узла от исходно­го узла до узла назначения. Значение Uj для каждого узла рассчи­тывается по формуле:

Uj = min{ U_i + d_ij }

Процедура заканчивается, когда получено значение U_n для узла назначения.

Кратчайший маршрут от исходного узла до узла назначения определяется, начиная с узла назначения, путем прохождения узлов в обратном направлении по дугам, на которых реализова­лись минимальные значения расстояний на каждом шаге.

Пример. Определить кратчайшее расстояние между узлами x₁ и х₇.

U₁=0;

U₂ = U₁ + d₁₂ = 0 + 2 = 2;

U₃= U₁ + d₁₃ = 0 + 4 = 4;

U₄= min{ U₁ + d₁₄, U₂+d₂₄, U₃+d₃₄} = min{0 + 10,2 + 11,4 + 3} = 7;

U₅= min{ U₂ + d₂₅, U₄ + d₄₅ } = min{2 + 5, 7 + 8} = 7;

U₆ = min{ U₃ + d₃₆, U₄+d₄₆ } = min{4+ 1, 7 + 7} = 5;

U₇ = min{ U₅ + d₅₇, U₆+d₆₁ } = min{7 + 6, 5 + 9} = 13.

Дата добавления: 2014-12-16