Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши

Напомним, что множество называется односвязным, если любой замкнутый контур, лежащий в 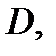можно стянуть в точку, не выходя из 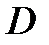. Множество 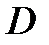называется 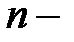связным, если его граница состоит из попарно не пересекающихся между собой замкнутых контуров. Например, на рисунке A изображена односвязная область, на рисунке B – 4-связная область (одна внешняя граница и три внутренних границ). При этом будем говорить, что направление на границе является положительным ( – положительно ориентирована), если при её обходе область остаётся слева. Например, на рисунке C граница двухсвязной области положительно ориентирована. Ориентация, противоположная положительной, называется отрицательной.

Теорема Коши для односвязной области. Пусть область 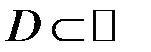односвязная и функция аналитична в Тогда каков бы ни был кусочно-

гладкий замкнутый контур 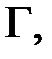лежащий внутри интеграл от по равен нулю.

Доказательство. Вычислим интеграл

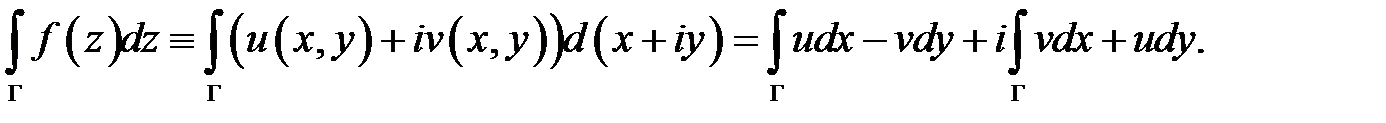
Воспользуемся формулой Грина:

где 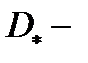область, охватываемая контуром Будем иметь

(здесь в квадратных скобках выписаны условия Коши-Римана, которые выполняются, так как функция 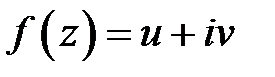аналитична в области ). Теорема доказана.

Теорема Коши для многосвязной области. Пусть область связна,причем её внешняя граница, а её внутренние границы, обходимые все против часовой стрелки. Пусть функция 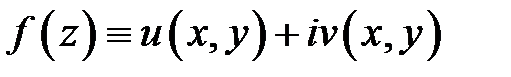аналитична в Тогда имеет место равенство

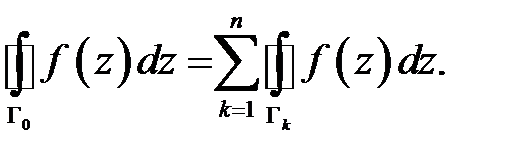
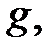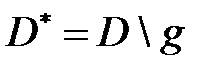Доказательство проведём для двухсвязной области Сделаем разрез соединяющий внутреннюю и внешнюю границы и Тогда область будет односвязной, а замкнутый контур 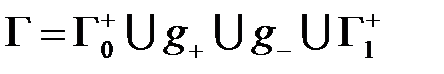лежит в Значит, для этого контура справедлива предыдущая теорема: Применяя свойство аддитивности интеграла, будем иметь

Рис. 10

Учитывая, что приходим к равенству

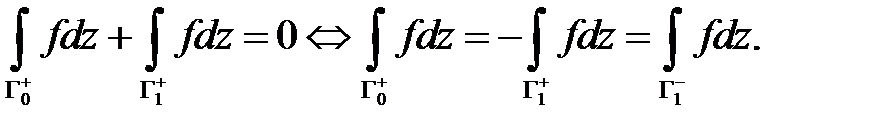
Остаётся учесть, что здесь контуры и 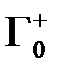обходятся против часовой стрелки. Теорема доказана.

И, наконец, сформулируем без доказательство следующее важное утверждение.

Интегральная теорема Коши. Пусть функция 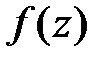аналитична в односвязной области 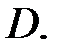Тогда какова бы ни была точка 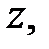лежащая внутри области 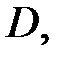и замкнутый кусочно-гладкий контур 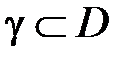, охватывающий точку 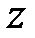и обходимый против часовой стрелки, справедлива интегральная формула Коши

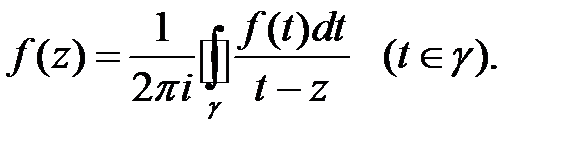
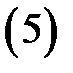
При этом функция 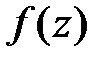имеет всюду в производные любого порядка, для которых справедлива формула

.

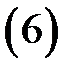
Замечание 1. Если функция аналитична в замкнутой ограниченной области с кусочно гладкой границей то в качестве контура в (6) можно взять границу Тогда из (5) вытекает, что аналитическая в 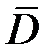функция полностью определяется своими значениями на границе Таким свойством действительные функции не обладают.

Интегральная формула Коши имеет многочисленные применения, о которых будет сказано в дальнейшим. Рассмотрим несколько примеров.

Пример 1. Вычислить

Решение. Внутри окружности 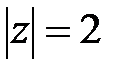знаменатель дроби обращается в нуль в точке 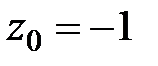. Для удобства применения формулы (5) перепишем интеграл в виде

.

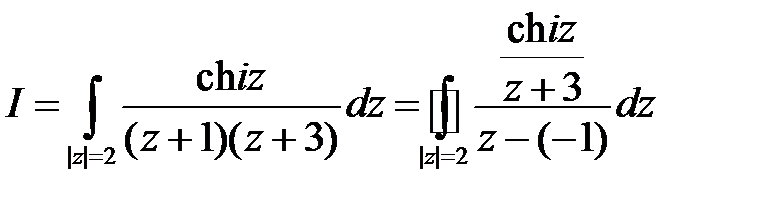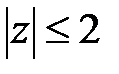Здесь и аналитична в круге . Тогда .

Пример 2. Вычислить 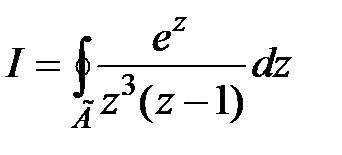: по

а) контуру ; б) .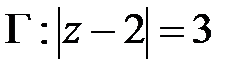

Решение. а) В круге 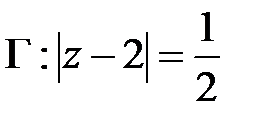функция 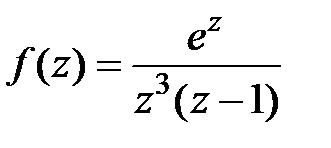аналитична. Следовательно, по теореме Коши для односвязной области получаем, что .

б) Так как внутри контура интегрирования знаменатель подынтегральной функции обращается в нуль в точках и 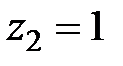, то для того, чтобы стало возможным применить формулу (5), рассмотрим многосвязную область (рис. 11), ограниченную окружностью и внутренними контурами и .

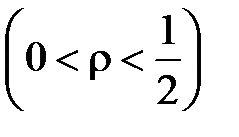Рис. 11

Тогда в области 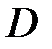функция является аналитической, и по теореме Коши для многосвязной области можно записать: . Для вычисления интегралов справа применим формулу (5):

;

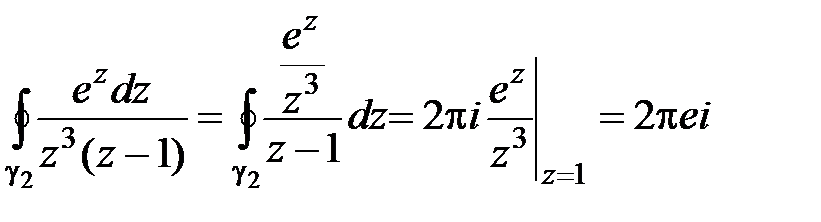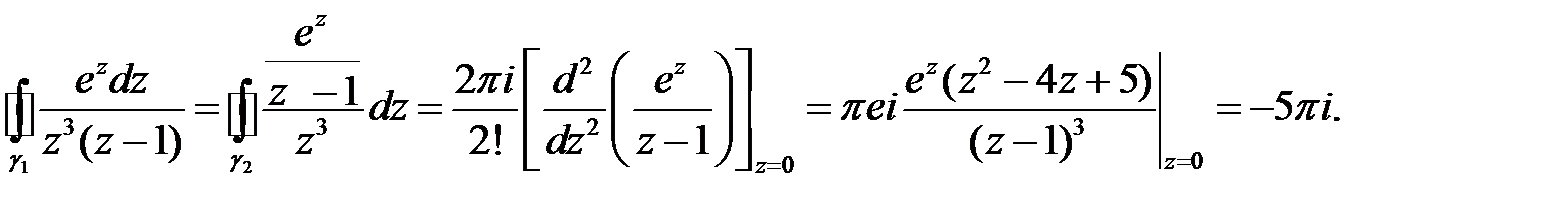
Таким образом, .

Дата добавления: 2014-11-29