Метод быстрой сортировки

Основная причина медленной работы алгоритма сортировки простыми включениями заключается в том, что все сравнения и обмены между ключами в последователь­ности элементов происходят для пар из соседних элементов. При таком способе требуется довольно большое время, чтобы поставить ключ, находящийся не на месте, в нужную позицию в сортируемой последовательности.

К.Хоор изобрел и весьма эффективно применил идею сравнения пары элементов, находящихся далеко друг от друга в последовательности. Это значительно сократило время сортировки. Для того чтобы понять этот алгоритм целесообразно рассмотреть следующий пример.

Предположим, что мы хотим отсортировать последовательность чисел из первой строки на рис.6.2. Начнем с предположения, что первый ключ в этой последовательности (38) служит хорошей аппрок­симацией ключа, который в конечном счете появится в середине от­сортированной последовательности. Используем это значение в ка­честве ведущего элемента, относительно которого ключи могут ме­няться местами, и продолжим следующим образом. Устанавливаем два указателя I и J, из которых I начинает отсчет слева (I=1), а J — справа в последовательности (J=N). Сравниваем аi и аj. Если ai<=aj, то устанавливаем J=-J—1 и проводим следующее сравнение. Продолжаем уменьшать J до тех пор, пока не достигнем ai>=aj. Тогда поменяем местами аi и аj (рис. 6.2, строка 5, обмен ключей 38 и 04), устанавливаем I=I+1 и продолжаем увеличивать I до тех пор, пока не получим ai>aj. После следующего обмена (строка 10, 79,38 поменялись местами) снова уменьшаем J. Чередуя уменьшение J и увеличение I, продолжаем этот процесс с обоих концов последовательности к «сере­дине» до тех пор, пока не получим I=J.

рис.6.2 Начальные шаги алгоритма метода быстрой сортировки.

Теперь имеют место два факта. Во-первых, ключ (38), который сначала находился в первой позиции, к этому времени занимает над­лежащее место в сортируемой последовательности. Во-вторых, все ключи слева от этого элемента будут меньшими, а все ключи справа — большими.

Ту же процедуру можно применить к левой и правой подпоследо­вательностям для окончательной сортировки всей последователь­ности. Последняя строка (с номером 22) рис.6.2 показывает, что когда будет получено I=J, то I=7. После этого процедура снова применяется к подпоследовательностям (1,6) и (8,16).

Рекурсивный характер алгоритма наводит на мысль, что следует значения индексов крайних элементов большей из двух неотсортиро­ванных подпоследовательностей (8,16) поместить на стек и затем пе­рейти к сортировке меньшей подпоследовательности (1,6).

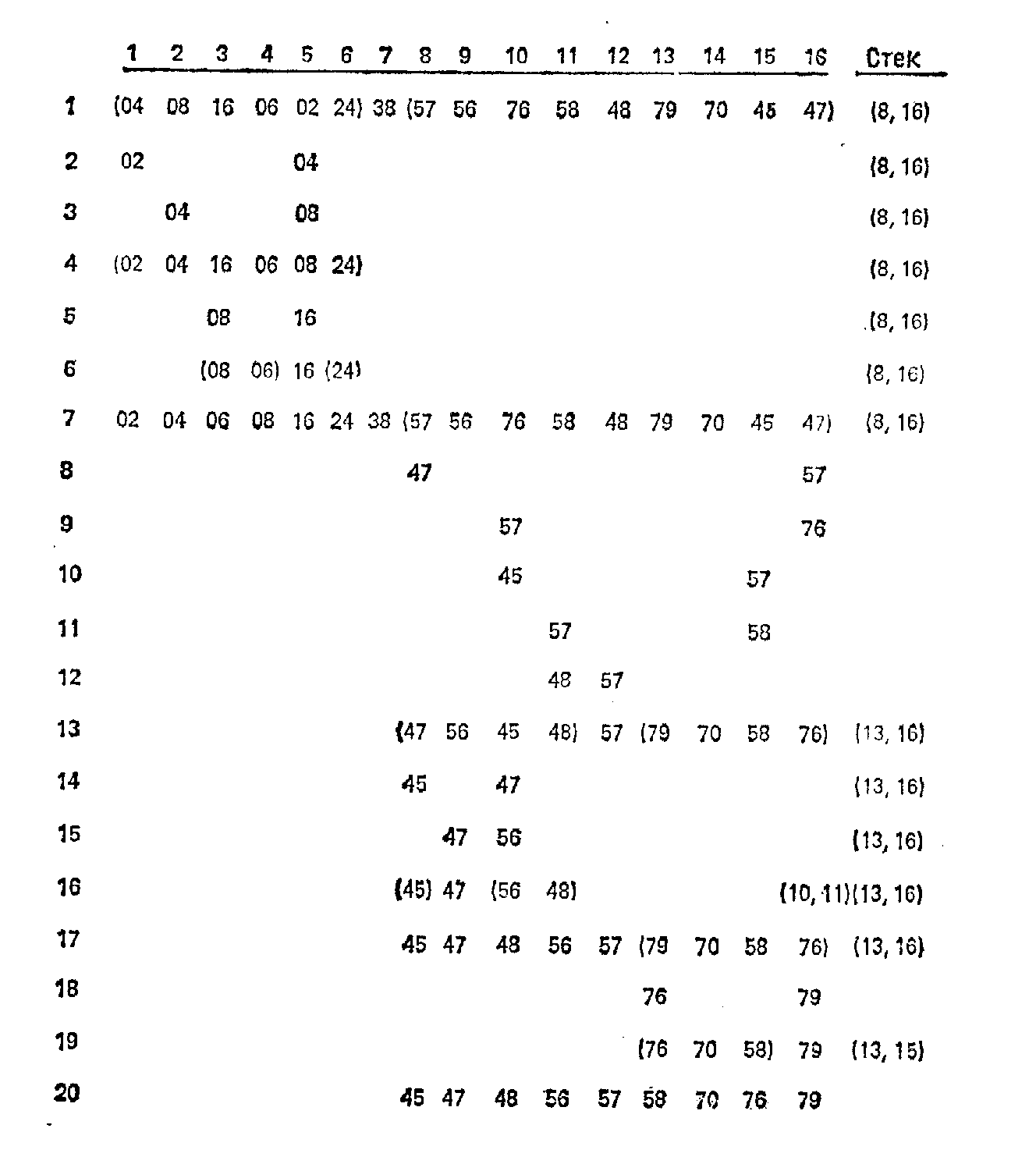
рис. 6.3. Завершение работы алгоритма быстрой сортировки.

В строке 4 на рис. 6.3 число 04 перешло в позицию 2 и сорти­ровке подлежат подпоследовательности (1,1) и (3,6). Так как (1,1) уже отсортирована (число 02), сортируем (3,6), что в свою очередь ведет к строке 6, в которой подлежат сортировке (3,4) и (6,6). В строке 7 подпоследовательность (1,6) отсортирована. Теперь извле­каем (8,16) из стека и начинаем сортировку этой подпоследователь­ности. В строке 13 находятся подпоследовательности (8, II) и (13, 16), которые надо отсортировать. Помещаем (13, 16) на стек, сортируем (8,11) и т. д. В строке 20 последовательность целиком отсортирована.

Математически доказано, что последовательность с большим числом элементов таким алгоритмом сортируется быстрее, чем методом сортировки простым включением, но если число элементов мало, то быстродействие рассмотренного метода значительно падает. В данном разделе мы не будем исследовать почему это происходит, а только укажем это. Строгие математические расчеты показывают, что для последовательностей с числом элементов больше 9 метод быстрой сортировки оказывается более быстродействующим. Если же число элементов меньше 9, то более быстродействующим оказывается метод простым включением.

Следовательно, большие массивы данных целесообразно обрабатывать методом быстрой сортировки, а для массивов данных с числом менее 9 с помощью метода прямого включения. На практике, для больших последовательностей, выгоднее применять оба эти метода для одной последовательности данных. Смысл такого применения заключается в том, что вначале последовательность обрабатывается методом быстрой сортировки, а потом когда размер подпоследовательностей станет меньше 9 данных, обработка продолжается методом прямого включения.

Дата добавления: 2014-12-16