Лекция 7

Коды Хемминга

В разработке и создании ряда помехоустойчивых кодов существенная роль отводится различным способам проверки на четность принимаемых кодовых комбинаций. В начале 50-х годов Хеммингом был предложен код, в котором контрольные символы размещались в кодовой комбинации не произвольно, а на строго определенных местах, что, естественно, облегчало декодирование.

Была разработана система проведения проверок правильности переданного кодированного сообщения, включающая алгоритм определения синдрома ошибки, указывающего не только на наличие ошибки, но и номер искаженной кодовой позиции.

Наибольшее распространение получили две модели кода Хемминга: код с обнаружением и исправлением одиночной ошибки (минимальное кодовое расстояние d = 3) и код с исправлением одиночной ошибки и обнаружением двойной (d = 4).

Для синтеза кода Хемминга необходимо решить следующие задачи:

Определить число контрольных символов, обеспечивающих заданные требования по помехозащищенности.

Установить, на каких позициях кодовой комбинации следует разместить контрольные символы и какие позиции займут информационные символы.

Собрав макет кодовой комбинации, определить значение каждого контрольного символа.

Составить кодовые комбинации, включающие как контрольные, так и информационные символы.

Дать алгоритм проверок, позволяющий установить наличие и место ошибки.

Синтез кода с d = 3

При этом исходным, как правило, является число информационных символов n_и , которое, в свою очередь, определяется множеством сообщений 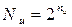. Иногда может задаваться общее число символов в кодовой комбинации n.

Первая задача.

Определить число контрольных символов n_к.

Для этого, если задано n или n_и , необходимо воспользоваться соответственно формулами

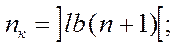(1)

, (2)

где ] b [ - знак округления до ближайшего большего целого числа.

Вторая задача.

Определить места, на которых в общей кодовой комбинации должны располагаться эти контрольные разряды.

Контрольные символы должны составить двоичное число (синдром ошибки), которое бы указывало номер ошибочной позиции.

В результате первой частной проверки на четность получается символ первого (младшего) разряда синдрома, в результате второй проверки - символ второго и т. д.

Итак, если синдром ошибки представить в виде двоичного четырехзначного числа и рядом записать соответствующие десятичные эквиваленты, то получим таблицу 1.

Десят-й эквив-т	Синдром ошибки

Выпишем последовательно в виде небольшой таблицы номера позиций, участвующих в каждой проверке на четность.

В первой проверке должны участвовать те позиции, которые содержат единицу в младшем разряде. Исходя из табл. 1, это будут 1, 3, 5, 9,.....

В второй проверке должны участвовать те позиции, которые содержат единицу во втором разряде. По табл. 1, это будут 2, 3, 6, 7,.....

В третьей проверке должны участвовать 4, 5, 6, 7,.... позиции.

В результате получим таблицу 2.

Номер проверки	Номера поз-й, охватыв-х этой проверкой
Первая
Вторая
Третья

Анализируя таблицу 2 можно заключить, что контрольные символы К_m должны размещаться на следующих позициях: К₁ на позиции 1, т.е. 2⁰;

К₂ на позиции 2, т.е. 2¹; К₃ на позиции 4, т.е. 2²; К₄ на позиции 8, т.е. 2³;

К_m на позиции 2^m.

Третья задача.

Определить значение контрольных символов. Составляется макет кода Хемминга. Пусть n_и =4, n_к = 3, n = 7. Тогда в общем виде он выглядит следующим образом:

Номера позиций 1 2 3 4 5 6 7

Символы К₁ К₂ И₃ К₃ И₂ И₁ И₀,

где И_i - информационные символы.

Алгоритм определения контрольных символов

Определение значения К_1. Составляется сумма по модулю 2 всех символов, включая и К₁, размещенных на позициях 1, 3, 5, 7, 9,..., охватываемых первой проверкой, т.е.

К₁ Å И₃ Å И₂ Å И₀. (3)

Значение символа К₁ определяется из условия обращения суммы (3) в нуль, т.е. из условия четности. Если число единиц (без К₁) нечетное, то К₁=1, если четное, то К₁=0.

Определение значения К_2. Составляется сумма по модулю 2 всех символов, включая и К₁, размещенных на позициях, охватываемых второй проверкой, т.е.

К₂ Å И₃ Å И₁ Å И₀. (4)

Значение символа К₂ определяется из условия обращения суммы (4) в нуль, т.е. из условия четности. Если число единиц (без К₂) нечетное, то К₂=1, если четное, то К₂=0.

Определение значения К_3. Составляется сумма по модулю 2 всех символов, включая и К₃, размещенных на позициях, охватываемых третьей проверкой т.е.

К₃ Å И₂ Å И₁ Å И₀. (5)

Символ К₃ одолжен обращать в нуль двоичную сумму (5).

Аналогично находятся К₄, К₅ и остальные символы, только для этого требуется проводить четвертую, пятую и остальные проверки и составлять соответствующие суммы.

Четвертая задача.

Составить кодовые комбинации. Для этого надо выписать все комбинации исходного безызбыточного двоичного кода и, пользуясь макетом кодового слова, а так же вычисленными на основании сумм (3), (4), (5) и так далее значениями контрольных символов К_m, записать все n _и комбинаций кода Хемминга.

Что касается пятой задачи - разработки алгоритма проверок, то она будет рассмотрена ниже, так как относится к декодированию кода Хемминга.

Рассмотрим пример синтеза кода Хемминга.

Пусть имеется ансамбль из 16 сообщений и его необходимо закодировать кодом Хемминга (d = 3).

Решение:

1) определяем число контрольных символов. Поскольку задан ансамбль сообщений N _и = 16, то задано число информационных символов n_и =lb16=4. Следовательно необходимо пользоваться формулой

Таким образом, n_к = 3, n = n_и + n_к = 4 + 3 = 7.

2) определяем позиции, на которых должны быть размещены эти три контрольных символа. Это будут позиции 1, 2 и 4 (см. таб. 2).

3) составляем таблицу комбинаций двоичного безызбыточного кода, не заполняя первую, вторую и четвертую графы. Всего комбинаций будет 16 (табл. 3).

4) находим значения контрольных символов:

для нулевой комбинации все К_j=0.

Для символа К_1.

Значение символа К₁ определяется из уравнения

К₁ Å И₃ Å И₂ Å И₀ =0.

а) К₁ = 0

б) К₁ Å 0 Å 0 Å 1 =0; К₁ = 1

в) К₁ Å 0 Å 0 Å 0 =0; К₁ = 0

г) К₁ Å 0 Å 1 Å 0 =0; К₁ = 1

д) К₁ Å 0 Å 1 Å 0 =0; К₁ = 1

е) К₁ Å 0 Å 1 Å 1 =0; К₁ = 0

Таблица 3.

Комби	Номера								Допол
нация	п/п	К1	К2	И3	К3	И2	И1	И0	Кдоп
а б в г д е

Для символа К_2.

Значение символа К₂ определяется из уравнения

К₂ Å И₃ Å И₁ Å И₀ =0.

а) К₂ = 0

б) К₂ Å 0 Å 0 Å 1 =0; К₂ = 1

в) К₂ Å 0 Å 1 Å 0 =0; К₂ = 1

г) К₂ Å 0 Å 1 Å 1 =0; К₂ = 0

д) К₂ Å 0 Å 0 Å 0 =0; К₂ = 0

е) К₂ Å 0 Å 0 Å 1 =0; К₂ = 1

Для символа К_3.

Значение символа К₃ определяется из уравнения

К₃ Å И₂ Å И₁ Å И₀ =0.

а) К₃ = 0

б) К₃ Å 0 Å 0 Å 1 =0; К₃ = 1

в) К₃ Å 0 Å 1 Å 0 =0; К₃ = 1

г) К₃ Å 0 Å 1 Å 1 =0; К₃ = 0

д) К₃ Å 1 Å 0 Å 0 =0; К₃ = 1

е) К₃ Å 1 Å 0 Å 1 =0; К₃ = 0

Проставляем значение контрольных символов в табл. 3. Код синтезирован. Поставленная задача решена. (Студенту предлагается в порядке упражнения самостоятельно завершить заполнение табл. 3).

На примере полученного кода Хемминга с d = 3 можно показать, как строится код Хемминга с d = 4, ïîçâîëÿþùèé îáíàðóæèâàòü äâóхêðàòíûå îшибки. Число контрольных символов в таком коде должно быть на единицу больше, т.е. для рассматриваемого примера n_к = 3 + 1 = 4, следовательно, код будет восьмипозиционный.

Принцип получения такого кода следующий:

* к каждой кодовой комбинации добавляется еще один дополнительный контрольный символ, позволяющий осуществить общую проверку на четность;

* значение дополнительного контрольного символа определяется исходя из наличия в каждой комбинации кода Хемминга (т.е. учитывая и контрольные символы) четного числа единиц. Таким образом, в нашей табл. 3 появляется еще одна графа К_доп;

* заполняем эту графу, т.е. определяем значение контрольных символов и размещаем их на последней (восьмой) кодовой позиции:

а) К_доп = 0

б) К_доп = 0

в) К_доп = 1

г) К_доп = 1

д) К_доп = 1

е) К_доп = 1

Дата добавления: 2014-12-16