Закон ослабления потока рентгеновских лучей

144.

143.

142.

141.

140.

139.

138.

137.

134.

129.

127.

126.

125.

124.

121.

119. 120.

119,120 ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ.ПОЛЯРИЗАЦИЯ СВЕТА.ЗАКОН МАЛЮСА. Электромагнитную волну,в кот. векторы Е и,=>,векторы В во вполне определенных плоскостях,наз. плоскополяризованной. Плоскость,проход-ая через электрич-ий вектор Е и направл-е распростран-я электромагн-ой волны,явл. плоскостью поляризации. Естеств-ый свет-идущий от Солнца,пламени,наколен.нити лампы…Прямая с черточ-ми или точками обознач-т луч плоскополяриз-го света.Луч света,сост-го из неполяризов-ой и поляризов-ой состав-щих и наз-го частичнополяризов-ым, причем соотнош-е числа стрелок и точек усл-но иллюстр-ет степень поляризации,т.е.долю интенсив-ти поляриз-ой составл-щей относ-но полной интенсив-ти света.Устройство,позвол-щее получать поляриз-ый свет из естеств-го,наз. поляризатором. Он пропускает только составл-щую вектора Е на некот-ую плоскость- главную плоскость поляриз-ра, кот. содерж.световой вектор Е и направл-е распростр-ия света.Поляризатор,использов-ый для анализа поляризов-го света,наз. анализатором. Если плоскополяриз-ый свет с амплитудой электрич-го вектора Е_о падает на анализатор,то он пропустит только составл-щую,равную Е=Е_оcos,где угол между глав-ми плоскостями поляриз-ра Р и анализатора А.Т.к. интенсивность света пропорц-на квадрату амплитуды колебаний,то получ.I=I_o ,где I_o-интенсивн-ть плоскополяризов-го света,пад-щего на анализатор,I-интенсивн-ть света,вышедшего из анализатора.Уравн-ие выраж-т закон Малюса. Из закона видно,что при повороте анализатора относ-но луча падающего плоскополяриз-го света интенсивн-ть прошедшего света измен-ся от 0 до I_o.Если при повороте анализатора вокруг падающего луча как оси вращ-ия интенсивн-ть прошедшего света не измен-ся,то свет естественный; если при этом интенсивн-ть измен-ся по закону,то падающий свет- плоскополяризов-ый. ”Поляризация света”-1)свойство света,характериз-еся пространств-но-временной упорядочен-тью ориентации электрич-го и магнит-го векторов;2)это процесс поляризов-го света.

122. ПОЛЯРИЗАЦИОННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ БИОЛОГИЧЕСКИХ ОБЬЕКТОВ. Поляризационный микроскоп аналогичен обычному биологич-микроскопу,но имеет поляризатор перед конденсором и анализатор в тубусе между объективом и окуляром.Предметный столик вращ-ся вокруг оптической оси микроскопа.Таким образом,объект освещают поляриз-ми лучами и рассматр-ют через анализатор.Если скрестить поляризатор и анализатор,то поле зрения будет темным.Анизотроп-е предметы изменяют поле зрения в соотв-ии с тем влиянием,кот. они окажут на направл-е плоскости колебаний поляризов-го света.Некот-ые ткани обладают оптич-кой анизотропией,=>,возможна полязац-ная микроскопия биолог-их объектов. Поляризов-ный свет можно использ-ать в модельных условиях для оценки механич-их напряжений, возник-щих в костных тканях. – Это явление фотоупругости,кот. заключ-ся в возникн-ии оптич-кой анизотропии в первонач-ном изотропных твердых телах под действием механич-их нагрузок.

123..Поляриметрия. Поляризационные приборы. Для р-ров был установлен кол-венный закон: _С, где С-конц-ция оптически активного в-ва, -толщина слоя р-ра, _- удельное вращение,кот-ое приблиз-но обратнопропорцион-но квадрату длины волны волны и зависит от темп-ры и св-тв р-рителя. Это соотнош-ие лежит в основе метода измерения конц-ции р-ренных в-тв (сахара). Этот метод (поляриметрия или сахариметрия) исп-зуют в медицине для определ-ия конц-ции сахара в моче, в биофизич-ких исслед-ниях, в пищевой промышл-сти.=> измерит-ные приборы – поляриметры или сахариметры. Поляриметр позволяет измерять удельное вращение. Используя различные светофильтры можно найти завис-ость удельного вращения от длины волны (дисперсия оптич-кой активности), для этих целей применяют спец.приборы – спектрополяриметры. Поляриметрию применяют как метод исслед-ния структурных превращений (в молекул-ной биофизике).

128.

130. Люминесценция (Л)–тепл. из­луч. тела,имеющее длительность,превы­шающ. период(10-15 с) излучаемых свет. волн.Св-ва: 1.Л. наблюд-ся в видимой или УФ областях спектра. 2.Л. наблюд-ся при любых температурах (холодное свечением). 3.Признак длительности (Вавилов) - для того, чтобы отличить Л. от других явлений вторичного свечения (отраже­ние и рассеяния света). 4.Люминесцируют электронно-возбужд. м-лы (ато­мы). Виды: 1.Л., вызванная заряжен. ч-цами: ионами — ионо-, электронами — катодо-, ядер­н. излуч. — радио-, рентген. и у-излуч. – рентгено-, фотонами видимого света — фотолюминесценции. Л., сопровожд. экзо­термич. хим. р-цию, - хемилюминесц. Фотолюминесц.: флуоресценцию (кратковрем. после­свечение) и фосфоресценцию (длительн. послесве­чение). Начальн. акт фотолюминесц. – возбужд. фотоном с энергией атома или м-лы. В одноатомн. парах и газах при низк. давлении, атом возвращ. в основное сост., излучая фотон света той же частоты. Это – резонансн. флуоресц. (возник. через 10-8 с после освещения в-ва, поэт. не явл. рассеянием). При ↑ давления или добавлении в люминесцир. пары инородн. газов (Н₂, О₂) резонанс. флуоресц. ↓ и появл. другие линии флу­оресц. Причина этого: возбужд. атомы сталк-ся с окруж. атомами или м-лами. → возбужден. атомы переходят в основн. сост., а окруж. ч-цы приобрет. кине­тич. энергию. Органич. м-лы, имеющ. сис. сопряженных двой­ных связей, в основн. (невозбужд.) сост. находятся в нижнем колебательном сост. электрон. уровня S₀. Распределение м-л по энергетич. уровням за счет тепл. энергии распределением Больцмана: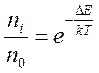

где n₀ и n_i — число м-л в основн. и возбужд. со­ст., ∆E_i — разность энергий для этих состояний, k — посто­янная Больцмана, Т — абсолют. температура. Под действием света может произойти возбуждение м-лы с переходом на разные колеба­т. уровни. Пути расходования энергии возбужде­ния: часть м-л отдает энергию окруж. ч-цам, нагре­вая тело; другая часть излуч. кванты флуоресценции, переходя на ка­кой-либо колебат. уровень. Каждый из этот процессов происх. с опред. вероятностью - квантовым выходом (φ_фл). Число излу­ченных квантов флуоресц. к числу поглощен. квантов (отношение потока флуоресц.)- (Ф_фл); поток поглощен­. света - I₀(1 - T)S, где I₀—интенсивн. возбуждающ. све­та, S — площадь поглощающ. поверхности, (1 - Т) — коэфф. поглощения:

Поток флуоресц. (Ф_фл) пропорци­онален коэфф. поглощ. (1 - Т), кот. нелинейно за­висит от концентрации. →флуоресц. завис. от концентрации нелинейно. Интенсивн. флуоресц. I_фл: I_фл = kI₀(1 - T)φ_фл = kI₀(1 – 10^{-ε Cl}) φ_фл

где k — коэффициент, определ. чувствительностью прибо­ра, Т = 10^{-ε Cl}.

Закон Стокса: спектр Л. сдвинут в длинновол­н. область относительно спектра поглощения того же соеди­нения. Причина сдвига спектров: электронный переход при поглощении происх. с нижнего ко­лебат. уровня основн. сост. на любые колебат. уровни возбужд. электрон. уровней (часть энергии возбуждения м-л переходит в теп­ло – волнист. стрелки), и они оказываются на нижнем колебат. уровне нижнего возбужд. элек­тронного сост.. Излучение происходит только с такого уров­ня на любые колебательные подуровни основного состояния. Дли­на стрелок, изображающих поглощательные и излучательные пе­реходы в молекуле, пропорциональна энергии. Форма спектра Л. (правило Каши) и квантовый выход Л. (закон Вавилова) не завис. от длины волны возбуждения Л. Причина: излучение Л. происх. всегда с нижнего колеба­т. уровня нижнего возбужд. электронного сост. Спектр фотолюминесценции по форме совпад. со спектрами других типов Л. данного вида м-л, т. е. форма спектра Л. не завис. от способа воз­буждения м-лы. Спектральное положение полосы флуоресц. завис. от длины сист. со­пряженных двойных связей I: чем больше I, тем большей длине волны соответст. максимум флуоресценции.

131..Медицинское применение люминесцентных методов исследования. К люминисцентным приборам относятся лазеры, которые используются в разных отрослях науки. Первый лазер был создан в 1960 году и являлся лазером с кристаллом рубина в качестве рабочей среды. Применение лазеров основано на свойствах их излучения: высокая монохроматичность, достаточно большая мощность, узость пучка и когерентность. Широкое применение лазеры нашли в хирургии, стоматологии, офтальмологии, дерматологии онкологии. Все лазеры, используемые в медицине, условно подразделяются на 2а вида: низкоинтенсивные (терапев-тические – не вызывают заметного деструктивного дейст-вия на ткани непосредственно во время облучения) и высо-коинтенсивные (хирургические).

131.Использ. флуорес­центно-меченых антител. Если добавить такие антитела к суспен­зии смеси клеток, то они связываются только с теми из них, на поверхности которых находятся специфические к данному анти­телу антигены. Возникает яркая флуоресценция определенных клонов клеток, хорошо видная в люминесцентных микроскопах, в кот. в отличие от обычных источников света, используют ртутные лампы высокого и сверхвысокого давлений и применяют два светофильтра. Один из них, расположенный перед конденсором, выделяет область спектра. Значения квантового выхода флуоресценции для разных ве­ществ сильно отличаются. Для флуоресцеина Ффл = 0,9, для бел­ков — варьирует в пределах 0,01—0,03. Флуоресцирующие соеди­нения удается с высокой чувствительностью обнаруживать в сложных смесях нефлуоресцирующих соединений. По флуоресценции удается обнаруживать грибковые повреждения волос и кожи, следовые количества наркотических веществ, на­чальные стадии порчи некоторых продуктов.

132. Хар-ка теплового излуч. Средняя мощность излучения за время, большее периода световых колебаний, - поток излучения Ф. В СИ - в ваттах (Вт). Поток излучения, испускаемый 1 м² поверхности, - энергетич. светимостью R_e (Вт/м²). Нагретое тело излучает электромагнитные волны различ. дли­ны волны. Выделим небольшой интервал длин волн от λ до λ+dλ. Энергетич. светимость, соответст. этому интервалу, про­порциональна ширине интервала: dR_λ=r_λdλ,где r_λ—спектральн. плотность энергетич. светимос­ти тела, = отношению энергетич. светимости узкого участка спектра к ширине этого участка, Вт/м³. Зависимость спектральной плотности энергетич. свети­мости от длины волны - спектр излуч. тела. Выражение для энергетич. светимости тела: R_e=∫r_λdλ. Способность тела поглощать энергию излучения хар-­ют коэфф. поглощения, = отношению потока из­луч., поглощенного данным телом, к потоку излуч., упав­шего на него: α=Ф_погл/Ф_пад . Т.к. коэфф. поглощения зави­сит от длины волны, то для монохроматич. излуч. определяют монохрома­тич. коэфф. поглощения: α_λ=Ф_погл(λ)/Ф_пад(λ). Коэффициенты поглощения могут при­нимать знач. от 0 до 1. Хорошо поглощают излуч. тела черного цвета: черная бумага, ткани, бархат, сажа, пла­тиновая чернь; плохо - тела с белой поверхно­стью и зеркала. Тело, коэффициент поглощ. кот. = 1 для всех длин волн (частот), наз. черным. Оно погло­щает все падающее на него излучение при любой темпера­туре. Черных тел в природе нет, это понятие — физич. абстрак­ция. Модель черного тела - маленькое отверстие в зам­кнутой непрозрач. полости. Луч, попавший в это отверстие, многократно отразившись от стенок, почти полностью будет поглощен. Тело, коэфф. поглощения кот. <1 и не зависит от длины волны света, падающ. на него, на­з. серым. Серых тел в природе нет, однако некоторые тела в определен­ном интервале длин волн излучают и поглощают как серые. Так, тело человека иногда считают серым, имеющим коэф­ф. поглощения приблиз. 0,9 для инфракрасной об­ласти спектра.

133. Закон Кирхгофа. Между спектральной плотностью энергетич. светимости и монохроматич. коэфф. поглощения тел сущ. определенная связь, кот. можно пояснить на следующем при­мере. В замкнутой адиабатной оболочке находятся 2 разных тела в условиях термодинамич. равновесия, при этом их темпера­туры одинаковы. Т.к. сост. тел не изменяется, то каждое из них излуч. и поглощ. одинаковую энергию. Спектр излу­чения каждого тела должен совпадать со спектром электромаг­нит. волн, поглощаемых им, иначе нарушилось бы термодина­мич. равновесие. Это означает, что если одно из тел излучает какие-либо волны, например красные, больше, чем другое, то оно должно больше их и поглощать. Количественная связь между излуч. и поглощ. была установлена Г. Кирхгофом в 1859 г.: при одинак. температу­ре отношение спектральной плотности энергетич. свети­мости к монохроматич. коэфф. поглощения одина­ково для любых тел, в том числе и для черных (закон Кирх­гофа): (r_λ/α_λ)₁=(r_λ/α_λ)₂=…=ε_λ/1, где ε_λ — спектральная плотность энергетической светимости чер­ного тела (индексы у скобок означают тела 1, 2 и т. д.). Закон Кирхгофа может быть записан и в таком виде: r_λ/α_λ= ε_λ. Отношение спектральной плотности энергетич. светимос­ти любого тела к его соответствующему монохроматич. ко­эфф. поглощения = спектральной плотности энергети­ч. светимости черного тела при той же температуре. r_λ=α_λε_λ. Т.к. для любого тела (нечерного) α_λ< 1, то спектральная плотность энергетич. светимости любо­го тела < спектральн. плотности энергетич. свети­мости черного тела при той же температуре. Черное тело при про­чих равных условиях является наиболее интенсивным источни­ком теплового излуч.. Eсли тело не поглощает какое-либо излуче­ние (α_λ = 0), то оно его и не излучает (r_λ= 0). Пользуясь законом Кирхгофа и зная из эксперимента спектр излучения черного тела ε_λ=f₁(λ), а также зависимость мо­нохроматич. коэфф. поглощения тела от длины вол­ны α_λ=f₂(λ), можно найти спектр излуче­ния тела r_λ = f₃(λ) = f₁(λ) • f₂(λ).

135.. Теории Бора. Постулаты. Первый постулат: атом и атомные сис. могут длительно пребывать только в опред. стационарных со­ст. Находясь в таких сост., атом не излучает и не по­глощает энергии. Стационарным сост. соответствуют диск­ретные значения энергии: E1, Е2,. Любое изменение энергии атома или атомной сис. связано со скачкообразным переходом из одного стационарного сост. в другое. Второй постулат: при переходе атома из одного сост. в другое атом испуск. или поглощает фотон частоты v, энергия кот. определяется разностью энергий Еi, Ек атомных состо­яний: hv = Ei - Ek. Переход из сост. с больш. энергией в сост. с мень­ш. энергией сопровождается излучением фотона. Обратн. про­цесс - при поглощении фотона. По теор. Б., электрон в атоме Н вращ. по круговой орбите вокруг ядра. Из всех возможных орбит стаци­онар. сост. соответствуют только тем, для кот. мо­мент импульса (орбитальный механич. момент) = цел. числу h/2π: mv_nr_n= h/2π, где n=1,2,3 и тд, m — масса электрона, v_n— его скорость на n-й орбите, r_n — ее радиус. На электрон, вращающ. по круговой орбите в атоме (ионе), действует кулоновская сила притяж. со стороны + заряженного ядра, кот., по 2 з-ну Ньютона, = произвед. массы электрона на центростремит. ускоре­ние: Ze·e/4πε_or_n²=Ze²/4πε_or_n²=mv_n²/r_n где е — заряд электрона, Ze — заряд ядра. Для водорода Z = 1, для водородоподобных ионов Z > 1. r_n =ε₀h²n²/πZe²m. Находим кинетич. энергию электрона: E_к=mv_n²/2=Ze²/8πε_or_n. Cумма кинетической и потенциальной энергий дает полную энергию электрона:E=Eк+Eп= Ze² /8πε_or_n – Ze²/4πε_or_n = - Ze²/8πε_or_n. Дискретные знач. энергии Е_п= -me⁴Z²/8ε_o²h²n². На основании 2 пост. Б. получил формулу, объясняющую сериальные закономернос­ти спектра атома H и водородоподобных ионов. ν = me⁴/8ε₀²h³[1/n_k²-1/n_i²]. Несмотря на успех теор. Б., не удалось объяснить раз­личия интенсивностей спектральных линий (почему одни переходы между энергетич. уровнями бо­лее вероятны, чем другие). Теор. Б. не раскрыла спектральн. закономерностей более сложн. атомных сис. Недостаток теор. Б. - ее внутр. противоречи­вость. Эта теория объединяла в себе положения принципиально отличных теорий: классич. и квантовой физики. В первой четверти двадцатого века стало ясно, что теория Бора должна быть заменена другой теорией атома, в связи с чем и по­явилась квантовая механика.

136. Волновая функция.

Гипотеза о том, что микрочастицы обладают волновыми свойствами, была высказана французским физиком-теоретиком Луи де Бройлем, за что он получил Нобелевскую премию A929). Согласно этой гипотезе, движение

микрочастиц с массой т и скоростью v подобно волновому процессу, длина волны которого определяется по формуле Л = h/mv, где h — постоянная Планка (h = 6,6 • 10~34 Дж-с). Для описания состояний микрочастиц в квантовой механике используют волновую функцию зависящую от координат и времени. Эта функция аналогична функции для механической волны (см. лекцию 7). Далее мы будем рассматривать только стационарное состояние, в котором энергия частицы имеет определенное (и не меняющееся со временем) значение. Для стационарного состояния волновую функцию можно представить в виде произведения двух сомножителей, 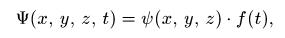) один из которых зависит только от координат, а другой только от времени. Для стационарного состояния зависимость от времени не существенна, и для описания используется только функция ф(х, у, z).

конечной шириной

Уравнение Шредингера Уравнение, определяющее волновую функцию (волновое уравнение), было составлено Э. Шредингером, австрийским физиком-теоретиком A887-1961). По своему значению это уравнение квантовой механики ана- логично 2-му закону Ньютона в классической механике, но нахождение его решений — задача во много раз более сложная. Поэтому мы рассмотрим только простейшую ситуацию, которая демонстрирует особенности стационарных состояний микрочастицы. Применительно к любому стационарному состоянию уравне- ние Шредингера записывается в следующем виде:

,

где т — масса частицы, Е и Еп — ее полная и потенциальная энергии. Рассмотрим одномерный случай, когда частица перемещается только вдоль оси ОХ. В этом случае уравнение C4.9) упрощается:

Потенциальная энергия Еп определяется воздействием силового поля, в котором находится частица.

145-150.. (в отдельном файле)

Рентгеновским называется электромагнитное излучение с длинами волн от 0,001 до 50 нанометров

В результате многих процессов пучек ослабляется в соотв. С Законом: Ф= 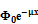, μ - линейный коэф. ослабл.Его можно представить в виде 3х слогаемых(Когерентное рассеяние,некогерентное и фотоэффект) μ= + +

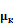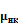Поток рентг.излуч. ослабл. пропорц. числу атомов в-ва,через кот. проходит.

Линейный коэф. ослабления зависит от плотности в-ва.

Поэтому используют массовый коэф. ослабл.,кот. = отнош. Линейного к плотности поглотителя и не зависит от плотности в-ва. = μ/р

Экспоненциальный закон ослабления пучка -фотонов выпол­няется приближенно, особенно при больших энергиях. Это обус­ловл. вторичными процессами, возник.при взаимод. -излучения с в-ом. Поток нейтронов тоже –ионизир. излуч, т.к. в результате взаимод. нейтронов с ядрами атомов обр.заряженные частицы и -излучение.

Дата добавления: 2014-12-16