Методы определения проницаемости пород

При измерении проницаемости по газу в выражении (1.4.6):

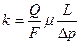
следует в качестве Q записать средний расход газа в условиях образца - 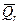, приведенный к среднему давлению в образце. Такая замена вызвана непостоянством объемного расхода газа при естественном уменьшении давления по длине образца. В результате вместо (1.4.6) имеем для определения газопроницаемости:

(1.4.24)

При малых длинах используемых образцов среднее давление по длине керна можно выразить следующим образом:

(1.4.25)

где Р₁ - давление газа на входе в образец, Р₂ - давление на выходе.

Полагая, что процесс расширения газа при фильтрации через образец происходит изотермически, по закону Бойля-Мариотта, используя (1.4.25), получим:

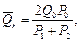(1.4.26)

где Q₀ - расход газа при атмосферном давлении.

Подставив (1.4.26) в (1.4.24), получим формулу для определения газопроницаемости пород в виде:

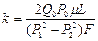(1.4.27)

Формула (1.4.27) может быть получена и из более строгих соображений:

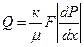
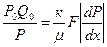
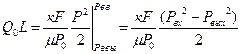
Из полученного выражения получим формулу, аналогичную (1.4.27).

Полученная формула соответствует закону Дарси при линейном потоке. Она лежит в основе определения абсолютной проницаемости в лабораторных условиях на приборе Товарова (см. дополнительный материал Приложения).

В случае необходимости определения проницаемости образцов при радиальной фильтрации жидкости и газа (случай скважиной фильтрации) пользуются несколько иными формулами. При фильтрации жидкости проницаемость определяется по формуле Дюпюи:

(1.4.28)

а при фильтрации газа:

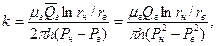(1.4.29)

где Q_ж - расход жидкости; Q_r, 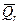- расход газа при атмосферном и среднем давлении в образце; - вязкости жидкости и газа; Р_н и Р_в - давление у наружной и внутренней поверхностей цилиндрического образца; r_н и r_в - наружный и внутренний радиусы цилиндра; h - высота цилиндра.

Для определения абсолютной проницаемости горных пород существуют разнообразные лабораторные установки. Однако принципиальные схемы их устройства большей частью одинаковы. Все они содержат одинаковые основные элементы: кернодержатель, позволяющий фильтровать жидкости и газы через пористую среду, приборы для измерения давления на входе и выходе из керна, расходомеры и приспособления, создающие и поддерживающие постоянный расход жидкости или газа через образец породы.

Вопросы для закрепления:

1. Что понимают под проницаемостью горных пород? Дайте определение проницаемости.

2. В каких единицах измеряется проницаемость?

3. Какая проницаемость называется абсолютной, фазовой, относительной?

4. В чем состоит линейный закон фильтрации в пористой среде?

5. Выведите формулу для определения проницаемости для газа.

6. Как определяется проницаемость в случае радиальной фильтрации? Дайте вывод формулы Дюпюи.

7. Как связаны проницаемость и пористость горных пород?

8. Какие существуют методы определения проницаемости?

9. Из каких основных элементов состоят лабораторные установки для определения проницаемости горных пород?

10. Как определяется проницаемость на аппарате Товарова?

Дата добавления: 2014-12-16