Упругие свойства горных пород

Касательных напряжений.

На рис. 6.2 показано, как под действием одной пары касательных напряжений τ _xy (рис. 6.2. а) и другой - τ _yx (рис. 6.2. б) будет выглядеть суммарный результат деформации грани (рис. 6.2. в). При этом прямой угол этой грани уменьшится на сумму углов γ₁ и γ₂: γ_xy= γ₁+γ₂. В случае однородных изотропных пород угол сдвига удвоится: γ_xy= 2γ₁.

Известно, что деформация тела обычно продолжается до тех пор, пока не наступит равновесие во всех точках между внешними и внутренними силами. Если после прекращения действия внешних сил деформация исчезает и тело принимает свою первоначальную форму, то такая деформация называется упругой. При этом действующие на тело внешние силы не превосходят определенного предела, называемого пределом упругости, а процесс является обратимым.

Неупругие деформации характеризуют необратимые процессы, связанные в горных породах, например с перегруппировкой зерен, скольжение их по поверхностям соприкосновения, разрушением и дроблением и т.д., так пористость не восстанавливается, но это характерно в основном для очень глубоко залегающих пластов весьма редко.

Упругость пород и пластовых жидкостей влияют на перераспределение давления в пласте. Сильно сжатые породы могут быть значительным источником энергии в пласте при снижении в них давления. Эффект упругости жидкости и пласта приводит к немгновенному перераспределению давления в пласте и по скорости этих длительных неустановившихся процессов можно судить, например, о проницаемости. Так, при упругом режиме снижение внутрипластового давления приводит к расширению жидкости или газа, сужению поровых каналов, так как внешнее давление остается постоянным.

Если тело полностью изотропно, то связь между напряжениями (σ) и деформациями (ε) выражается уравнениями, вытекающими из закона Гука:

,

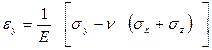, (1.6.3)

,

, , ,

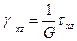где Е - модуль Юнга (коэффициент продольной упругости); G -модуль сдвига, ν -коэффициент Пуассона, равный отношению поперечной деформации сжатия к продольной.

Рассмотрим некоторые частные случаи.

1. Будем считать, что при геологическом формировании горной породы напряжение осуществлялось, в основном, в вертикальном (по оси z) направлении, т.е. e_z ≠ 0; e_x =e_y =0.

Решая систему уравнений (6.3.) относительно нормальных напряжений при этих условиях, получим:

, (1.6.4)

где 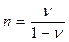называется коэффициентом бокового распора.

Учитывая, что коэффициент Пуассона лежит в пределах от 0 до 0,5, можно заключить, что даже при отсутствии перпендикулярных к оси z нормальных составляющих тензора напряжений, будут иметь место вполне ощутимые деформации горной породы в этих направлениях. Этот же эффект может наблюдаться в процессе бурения нефтяной скважины, приводящий преимущественно к одноосному сжатию породы.

2. Действие тензора напряжений всесторонне (это в большей степени относится к сформировавшейся и находящейся в равновесном состоянии горной породе), т.е. три взаимно перпендикулярных составляющих тензора напряжения равны между собой: σ_x=σ_y=σ_z=σ.

В этом случае из уравнений (1.6.3) получим:

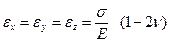. (1.6.5)

Тогда единица объема элемента породы будет изменена на величину:

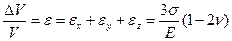
или 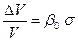(1.6.6)

Здесь 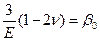- коэффициент объемного сжатия элемента горной породы, который можно определить экспериментально по модулю Юнга (Е) и коэффициенту Пуассона.

Для большинства изученных пород нефтяных месторождений уменьшение или увеличение объема образца связано с изменением пластового давления, следовательно, выражение (6.6) можно представить в виде:

, (1.6.7)

где ∆V_обр - изменение объема образца при изменении пластового давления на ∆P.

В.Н. Щелкачев предложил различать три коэффициента сжимаемости пород:

1. - коэффициент сжимаемости образца; (1.6.8)

2. - коэффициент сжимаемости пор; (1.6.9)

3. - коэффициент сжимаемости среды. (1.6.10)

Из них наибольший интерес представляет коэффициент сжимаемости (объемной упругости) среды , который характеризует относительное (по отношению ко всему объему V_обр) изменение объема порового пространства при изменении давления на 1Па.

Для нефтесодержащих пород =(0.3÷2)10^-10 Па^-1.

Из (6.9) и (6.10) следует, что 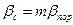. Поскольку всегда m <1, поэтому .

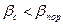Аналогом 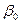для жидкости является коэффициент сжимаемости , определяемый в условиях изотермической фильтрации из выражения:

. (1.6.11)

Для пресной воды 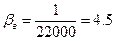∙10^-10 Па^-1.

Для нефти в пластовых условиях 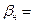(7÷30)10^-10 Па^-1.

В теории упругого режима пласта принято пользоваться более общим коэффициентом - коэффициентом упругоемкости пласта:

β^*= mβ_ж + β_с. (1.6.12)

И хотя обычно коэффициент сжимаемости среды βс меньше коэффициента сжимаемости жидкости β_ж, но т.к. m <1, то оба слагаемых в уравнении (6.12) могут быть вполне равнозначными.

В трещиноватых коллекторах аналогично с β_с введен коэффициент сжимаемости пласта при сокращении трещиноватой среды

На рисунках 1.6.3 и 1.6.4 приведены возможные схемы установки по определению коэффициента сжимаемости горных пород.

По экспериментально определенным значениям коэффициентов сжимаемости можно определить значение пористости образца горной породы в реальных условиях. Действительно, из уравнения (1.6.8) легко получить:

,

где V и V₀ - значения объема образца при давлении p и p₀, соответственно.

Полагая, что в горной породе именно поры претерпевают наибольшее сжатие или растяжение, имеем:

.

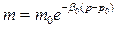Эта формула была предложена В.Н. Николаевским и позволяет переходить от лабораторной пористости (m₀) к пластовой (m).

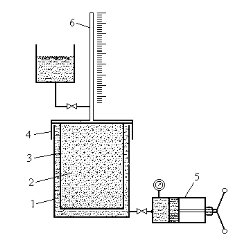
Рис. 1.6.3. Схема установки для определения коэффициента сжимаемости горных пород:

1-камера высокого давления, 2 – образец керна, 3 – эластичная непроницаемая оболочка, 4 – крышка, 5 – пресс для создания давления в камере,

6 – калиброванный капилляр для измерения объема жидкости, вытесняемой из сжимаемого образца.

Рис. 1.6.4. Схема установки для определения коэффициента сжимаемости горных пород:

1- измерительный пресс, 2 - вентиль 3 – термостат, 4 – образец керна, 5 - кернодержатель, 6 - образцовый манометр, 7 - датчик давления, 8 – микропресс.

1.6.3. Прочность и пластичность горных пород.

Большая часть горных пород при отсутствии высокого всестороннего давления как в условиях одноосного, так и сложного напряженного состояния при быстром нагружении или разгрузке в большом диапазоне реально существующих напряжений хорошо подчиняется закону Гука.

При медленном нагружении деформации почти всех горных пород отклоняются от закона Гука (возникают необратимые пластические деформации).

На рис. 1.6.5 приведены характерные кривые зависимости напряжения горных пород от деформации при различной скорости нагружения. Характер зависимости между s и e определяется продолжительностью действия нагрузки (t = 0 мгновенное нагружение, t =¥ — длительное). При s<s_s остаточной деформации не наблюдается в обоих случаях. Из рисунка видно, что чем длительнее процесс нагружения горной породы, тем больше в ней величина остаточной деформации. Если выделить на этих кривых линейный участок, соответствующий упругим деформациям с пределом упругости s_s, то можно оценить насколько долго сохраняются в данной горной породе упругие деформации относительно разрушающего напряжения s_{сж .}. Из экспериментальных исследований известны следующие соотношения: у глин s_s =10-15% s_сж; у твердых горных пород (песчаники, доломиты, известняки) упругие свойства сохраняются до s_s =70-75% s_сж.

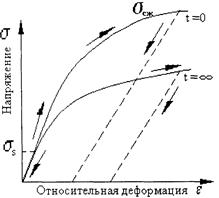
Рис. 1.6.5. Зависимость напряжения горных пород от деформации при различной скорости нагружения. ss – предел упругости; sсж. – разрушающее напряжение

В общем случае кривая, характеризующая связь напряжений и деформаций, имеет вид, представленный на рис. 1.6.6.

Рис. 1.6.6. Связь напряжений и деформаций горных пород с пределами: – упругости (точка В); – пластичности (точка Д); – прочности (точка Е). Точка С соответствует началу пластических деформаций на отрезке ВД.

Когда напряжение превышает предел упругости, тело Гука начинает разрушаться или пластически течь, переходя в тело Сен-Венана.

Сопротивление тела Гука разрушению и переходу в тело Сен-Венана, называют прочностью.

У песчаников прочность s_s =500 атм, известняков s_s =3500 атм. Такой большой диапазон обусловлен:

- кристаллической и агрегатной структурой горной породы,

- плотностью,

- составом,

- характером распределения цементирующего материала.

Один и тот же тип породы на разных глубинах и в разных географических районах может иметь разные механические свойства и прочность.

Горные породы оказывают:

наибольшее сопротивление сжатию,

наименьшее – растяжению (в 67 раз меньше, чем сжатию),

изгибу – в 4-6 раз меньше,

срезу в 2-4,5 раз меньше,

разрыву в 10-100 раз меньше.

Прочность горных пород на больших глубинах больше, чем при нормальных поверхностных условиях. Но прочность известняков и песчаников после проникновения воды уменьшается на 25-30%. Наиболее прочны мелкозернистые породы, что необходимо учитывать при проектировании буровых, взрывных и других работ, связанных с разрушением породы.

Пластичность. Почти все породы при различных условиях приложения нагрузки могут вести себя и как хрупкие, и как пластичные тела. При растяжении, изгибе, одноосном сжатии пластические свойства почти не проявляются.

При всестороннем сжатии многие горные породы, хрупкие при простых деформациях, приобретают пластические свойства (однако, чаще горные породы ограниченно пластичны).

Механизм пластических деформаций может быть различным (зависит от состава и свойств пород, условий залегания, действия нагрузки):

- вследствие межзерновых движений и явлений перекристаллизации;

- отдельные зерна могут двигаться независимо друг от друга (сцементированные зерна - песчаник, доломит);

В результате такого межзернового перемещения порода приобретает ограниченные пластические свойства.

Значительные пластические деформации претерпевают глины, глинистые породы, минералы типа каменной соли.

В песчаниках, известняках и доломитах пластические деформации могут возникнуть из-за появления микротрещин, позволяющих отдельным участкам пластов скользить и перемещаться вдоль плоскостей трещин.

Какова бы ни была природа ползучести и пластических деформаций – это происходит даже на сравнительно небольших глубинах.

На практике – с течением времени нарушенное поле естественных напряжений вокруг горных выработок и скважин восстанавливается, и давление, например, на обсадные колонны после окончания бурения долго возрастает, что объясняется проявлением ползучести и пластичности горных пород.

Дата добавления: 2014-12-16