Достичь звезд 2 страница

8. В настоящее время, помимо теории струн, активно развиваются два других подхода к объединению общей теории относительности и квантовой механики. Один из них, возглавляемый Роджером Пенроузом из Оксфордского университета, известен под названием теории твисторов. Другой подход, появление которого отчасти было инициировано работами Пенроуза, развивается Абхаем Аштекаром

Примечания 255

из университета штата Пенсильвания, и получил название метода новых переменных. Мы не будем рассматривать эти подходы в данной книге, однако появляются все более обоснованные предположения о том, что они могут иметь глубокую связь с теорией струн, и, возможно, все три подхода ведут к одному и тому же решению проблемы объединения общей теории относительности и квантовой механики.

Глава 6

1. Знающий читатель поймет, что в данной главе рассматривается только пертурбативная теория струн; выходящие за рамки теории возмущений аспекты обсуждаются в главах 12 и 13.

2. Интервью с Джоном Шварцем, 23 декабря 1997 г.

3. Схожие предположения были независимо высказаны Тамиаки Йонея, а также Коркутом Бардакчи и Мартином Гальперном. Значительный вклад в разработку теории струн на ранних этапах ее существования был также сделан шведским физиком Ларсом Бринком.

4. Интервью с Джоном Шварцем. 23 декабря 1997 г.

5. Интервью с Майклом Грином, 20 декабря 1997 г.

6. Стандартная модель предлагает механизм, дающий частицам массу, так называемый механизм Хиггса, получивший свое имя в честь шотландского физика Питера Хиггса. Однако с точки зрения объяснения значений масс частиц, задача здесь просто перекладывается на гипотетическую «частицу, дающую массу» — хиггсовский бозон. В настоящее время ведутся поиски этой частицы, но, опять же, даже если удастся обнаружить ее и определить ее свойства, они будут представлять собой входные данные для стандартной модели, не имеющие никакого теоретического объяснения.

7. Для читателей, имеющих математическую подготовку, укажем, что связь между модами колебаний струны и константами взаимодействия может быть более точно описана следующим образом. При квантовании струны ее возможные состояния, как и состояния любой квантово-механической системы, могут быть представлены векторами в гильбертовом пространстве. Эти векторы могут быть разложены по собственным значениям некоторого набора коммутирующих эрмитовых операторов. Среди этих операторов имеется гамильтониан, собственное значение которого дает энергию и, следовательно, массу этой колебательной моды, а также операторы, генерирующие различные калибровочные симметрии этой теории. Собственные значения этих последних операторов и дают константы взаимодействия, которые несут соответствующие колебательные моды струны.

8. Основываясь на догадках, сделанных в ходе второй революции в теории суперструн (обсуждаемой в главе 12), Виттен и Джо Ликкен (из Национальной лаборатории высокоэнергетических исследований) нашли маленькую, но возможную лазейку

в этом заключении. Используя ее, Ликкен предположил, что струны могут находиться под гораздо меньшим натяжением, и, следовательно, иметь гораздо больший размер, чем считалось первоначально. В действительности они могут оказаться столь большими, что могут быть обнаружены с помощью ускорителей частиц следующего поколения. Если эта маловероятная возможность окажется реальностью, открываются волнующие перспективы того, что многие замечательные следствия теории струн, обсуждаемые в этой и в последующих главах, смогут быть экспериментально проверены в течение ближайшего десятилетия. Но, как мы увидим в главе 9, даже в случае более «традиционного» сценария, разделяемого специалистами по теории струн, согласно которому струны обычно имеют длину порядка I0^--33 см, остаются косвенные методы экспериментальной проверки. 9. Знающий читатель поймет, что фотон, образовавшийся при столкновении электрона и позитрона, является виртуальным и, следовательно, должен быстро высвободить свою энергию путем образования пары частица-античастица. 10. Конечно, камера работает, улавливая отражающиеся от интересующих нас объектов фотоны и регистрируя их на фотопленке. Использование камеры в этом примере является символическим, поскольку мы не представляем себе фотонов, отражающихся от сталкивающихся струн. Мы просто хотим зарегистрировать на рис. 6.7 в всю историю взаимодействия. Сказав это, мы должны обратить ваше внимание на один тонкий момент, о котором умалчивает обсуждение в основном тексте. В главе 4 мы узнали, что квантовая механика может быть сформулирована с использованием фейнмановского метода суммирования по траекториям, в котором движение объектов анализируется путем суммирования вклада всех возможных траекторий, ведущих от выбранной начальной точки к некоторой конечной (каждой траектории в методе Фейнмана сопоставляется статистический вес). На рис. 6.6 и 6.7 мы показали вклад бесконечного числа возможных траекторий, по которым точечные частицы (рис. 6.6) или струны (рис. 6.7) следуют от начальной точки к пункту назначения. Однако приводимое в разделе обсуждение в равной мере применимо и к любой другой возможной траектории, а значит и ко всему квантово-механическому процессу в целом. (Фейнмановская формулировка квантовой механики точечных частиц с использованием подхода, основанного на суммировании по траекториям, была обобщена на случай теории струн в работах Стэнли Мандельстама из университета штата Калифорния в Беркли и Александра Полякова, в настоящее время работающего на физическом факультете Принстонского университета.)

Глава 7

1. Цитируется по книге R. Clark, Einstein: The Life and Times. New York: Avon Books, 1984, p. 287.

256 Примечания

2. Если говорить более точно, спин, равный 1/2, означает, что момент импульса электрона, связанный с его спином, составляет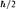

3. Открытие и развитие понятия суперсимметрии имеет непростую историю. В дополнение к тем, кто указан в тексте, основополагающий вклад внесли Р. Хааг, М. Сониус, Дж. Т. Лопушанский, Ю. А. Гольфанд, Е. П. Лихтман, Дж. Л. Шервэ, Б.Сакита, В. П. Акулов, Д. В. Волков и В. А. Сорока. Некоторые из их работ вошли в обзор Rosanne Di Stefano, Notes on the Conceptual Development of Supersymmetry. Institute for Theoretical Physics, State University of New York at Stony Brook, preprint ITP-SB-887S.

4. Для читателя, имеющего математическую подготовку, заметим, что это расширение включает дополнение обычных декартовых координат в пространстве-времени новыми, квантовыми координатами, скажем и и v, которые антикоммутируют: и х v — —v x и. Это позволяет рассматривать суперсимметрию как симметрию относительно трансляций в кванюво-механическом расширении пространства-времени.

5. Для читателя, интересующегося деталями этого технического вопроса, заметим следующее. В примечании 6 к главе 6 мы упоминали, что стандартная модель вводит «частицу, даюшую массу», хиггсовский бозон, которая генерирует измеряемые экспериментально массы элементарных частиц, перечисленных в табл. 1.1 и 1.2. Для того чтобы эта процедура работала, хиггеовская частица сама по себе не должна быть слишком тяжелой: проведенные исследования показывают, что ее масса, во всяком случае, не должна превышать примерно I 000 масс протона. Однако окаилось, что квантовые флуктуации могут вносить значительный вклад в массу хиггеовской частицы: это, в принципе, может приводить к массам, близким к планковской. Тем не менее теоретикам удалось установить, что можно избежать этого результата, указывающего на серьезный дефект стандартной модели, путем тонкой настройки некоторых параметров стандартной модели (прежде всего так называемой голой массы хиггеовской частицы) с точностью порядка 10^--15. что позволяет нейтрализовать влияние квантовых флуктуации па массу хиггсовской частицы.

6. Один тонкий момент, относящийся к рис. 7.1, состоит в том, что на этом рисунке интенсивность слабого взаимодействия занимает промежуточное положение между интенсивностью сильного и электромагнитного взаимодействия, хотя ранее говорилось, что она слабее всех. Объяснение этому можно найти в табл. 1.2, из которой видно, что частицы-переносчики слабого взаимодействия являются достаточно массивными, тогда как частицы, передающие сильное и электромагнитное взаимодействие, являются безмассовыми. В действительности интенсивность слабого взаимодействия (определяемая соответствующей константой — идея, с которой мы столкнемся в главе 12) является такой, как показано на рис. 7.1, но массивная частица, передающая это взаимодействие, довольно пассивно выполняет свои функции, что приводит

к уменьшению интенсивности этого вида взаимодействия. В главе 14 мы увидим, как вписывается в картину рис. 7.1 гравитационное взаимодействие.

7. Эдвард Виттен, из цикла лекций в память Хайнца Пагельса. г. Аспен, Колорадо, 1997 год.

8. Углубленное обсуждение этой и ряда других смежных идей приведено в книге Steven Weinberg, Dreams of a Final Theory. (Рус. пер.: Вайнберг С. Мечты об окончательной теории. М.: УРСС. 2004.)

Глава 8

1. Эго простая идея, однако, поскольку несовершенство нашего обычного языка приводит иногда к недопониманию, приведем два пояснения. Во-первых, мы считаем, что муравей живет на поверхности Садового шланга. Если бы муравей мог зарываться вглубь шланга, т. е. если бы он мог проникать внутрь резины, из которой сделан шланг, нам бы потребовалось три числа, чтобы указать его местоположение, поскольку нужно было бы указать, как глубоко он закопался. Однако если муравей живет только на поверхности шланга, то чтобы указать его положение, достаточно двух чисел. Отсюда следует необходимость второго пояснения. Даже тогда, когда муравей живет на поверхности шланга, мы можем, если захотим, указывать его положение с помощью трех чисел: обычных положений в направлениях влево-вправо, вперед-назад и вверх-вниз в нашем привычном трехмерном пространстве. Однако когда известно, что муравей живет на поверхности шланга, два числа, упомянутые в тексте, представляют собой минимальный набор величин, однозначно определяющих положение муравья. Именно это имелось в виду, когда мы говорили, что поверхность шланга двумерна.

2. Как ни удивительно, физики Савас Димопулос, Нима Аркани-Хамед и Гия Двали, основываясь на более ранних догадках Игнатиоса Антониадиса и Джозефа Ликкена, смогли показать, что даже если бы свернутые дополнительные измерения были столь велики, что достигали размера в один миллиметр, они могли бы оставаться необнаруженными экспериментально. Причина состоит в том, что ускорители частиц исследуют микромир с помощью сильного, слабого и электромагнитного взаимодействий. Гравитационное взаимодействие, которое при технологически достижимых энергиях остается чрезвычайно слабым, обычно игнорируется. Однако Димопулос с коллегами показали, что свернутые измерения оказывают влияние преимущественно на гравитационное взаимодействие (что выглядит вполне правдоподобно в теории струн); этот эффект вполне мог быть пропущен во всех экспериментах, выполненных до настоящего времени. В ближайшем будущем с использованием высокоточной аппаратуры будут проведены новые эксперименты по изучению гравитационных эффектов, предназначенные для поиска таких «крупных» свернутых измерений. Положительный результат будет означать одно из величайших открытий в истории человечества.

Примечания 257

3. Edwin Abbott, Flatland, Princeton: Princeton University Press, 1991. (Рус. пер.: Эббот Э. Флатляндия. М.: Амфора, 2001.)

4. Письмо А. Эйнштейна к Т. Калуце. Цитируется по книге: Abraham Pais, Subtle Is the Lord. New York: Oxford University Press, 1982, p. 330. (Рус. пер.: Пайс А. Научная деятельность и жизнь Альберта Эйнштейна. М.: Наука, Физматлит, 1989.)

5. Письмо А.Эйнштейна к Т. Калуце. Цитируется по статье: D. Freedman and P. van Nieuwenhuizen, The Hidden Dimensions of Spacetime, Scientific American, 252(1985), 62.

6. Там же.

7. Физики установили, что в многомерную формулировку труднее всего включить такое понятие стандартной модели как киральность. Поэтому, чтобы не перегружать обсуждение, мы не стали рассматривать это понятие в основном тексте. Для читателей, интересующихся этим вопросом, дадим здесь его краткое описание. Представьте, что кто-то показывает вам фильм, демонстрирующий некоторый научный эксперимент, и предлагает необычное задание — определить, показывает ли фильм сам эксперимент или его отражение в зеркале. Поскольку оператор был очень опытным, никаких признаков наличия зеркала на ленте не видно. Можете ли вы решить эту задачу? В середине 1950-х гг. теоретические работы Т. Д. Ли и Ч. Н.Янга, а также экспериментальные результаты Ц. С. By и ее коллег показали, что вы можете решить эту задачу, если на пленке снят подходящий эксперимент. А именно, их работы доказали, что законы мироздания не обладают полной зеркальной симметрией в том смысле, что зеркальные аналоги некоторых процессов, определяемых слабым взаимодействием, не могут существовать в нашем мире, даже если исходные процессы существуют. Таким образом, если, просматривая фильм, вы увидите, что он демонстрирует один из таких запрещенных процессов, вы будете знать, что наблюдаете зеркальное отражение, а не сам эксперимент. Поскольку зеркальное отражение меняет местами левое и правое, работы Ли, Янга и By показали, что Вселенная не обладает полной симметрией левого и правого, или, используя специальную терминологию, что Вселенная является киральной. Именно это свойство стандартной модели (в частности, слабого взаимодействия) физики считали почти невозможным включить в теорию супергравитации высших размерностей. Чтобы избежать недоразумений, отметим, что в главе 10 мы будем обсуждать концепцию теории струн, известную под названием «зеркальной симметрии», но там слово «зеркальная» будет использоваться в совершенно ином смысле.

8. Для читателя, имеющего математическую подготовку, отметим, что многообразие Калаби—Яу представляет собой комплексное кэлерово многообразие с нулевым первым классом Черна. В 1957 г. Калаби высказал предположение, что каждое такое многообразие допускает Риччи-плоскую метрику, а в 1977 г. Яу доказал справедливость этого предположения.

9. Эта иллюстрация была любезно предоставлена Эндрю Хэнсоном из университета штата Индиана, она была создана с использованием графического пакета Mathematica 3-D.

10. Для читателя, имеющего математическую подготовку, заметим, что это конкретное пространство Калаби—Яу представляет собой действительное трехмерное сечение гиперповерхности пятого порядка в комплексном проективном четырехмерном пространстве.

Глава 9

1. Edward Witten, Reflections on the Fate of Spacetime, Physics Today, April 1996, p. 24.

2. Интервью с Эдвардом Виттеном, 11 мая 1998 г.

3. Sheldon Glashow and Paul Ginsparg, Desperately Seeking Superstrings? Physics Today, May 1986, p. 7.

4. Sheldon Glashow. Опубликовано в The Supervorld I, ed. A. Zichichi, New York: Plenum, 1990, p. 250.

5. Sheldon Glashow, Interactions, New York: Warner Books, 1988, p. 335.

6. Richard Feynman. Опубликовано в Superstrings: A Theory of Everything? ed. Paul Davies and Julian Brown, Cambridge, Eng: Cambridge University Press, 1988.

7. Howard Georgi. Опубликовано в The New Physics, ed. Paul Davies, Cambridge: Cambridge University Press 1989, p. 446.

8. Интервью с Эдвардом Виттеном, 4 мая 1998 г.

9. Интервью с Кумруном Вафой, 12 января 1998 г.

10. Цитируется по книге: Robert P. Crease and Charles С. Mann, The Second Creation. New Brunswick, N. J.: Rutgers University Press, 1996, p. 414.

11. Интервью с Шелдоном Глэшоу, 28 декабря 1997 г.

12. Там же.

13. Интервью с Говардом Джорджи, 28 декабря 1997 г. Во время интервью Джорджи также отметил, что экспериментальное опровержение предсказанного распада протонов, которое следовало из предложенной им и Глэшоу первой теории великого объединения (см. главу 7), сыграло существенную роль в его нежелании принять теорию суперструн. Он горько заметил, что его теория великого объединения требует намного больших энергий, чем любая другая теория, когда-либо выносившаяся на суд, и когда его предсказание оказалось неверным, когда «он был нокаутирован природой», его отношение к изучению физики чрезвычайно высоких энергий резко изменилось. Когда я спросил его, не будет ли для него экспериментальное подтверждение теории великого объединения стимулом включиться в наступление на область планковских масштабов, он ответил: «Да, очень может быть»,

14. David Gross, Superstrings and Unification. Опубликовано в Proceedings of the XXIV International Conference on High Energy Physics, ed. R. Kotthaus and J. Kuhn. Berlin: Springer-Verlag, 1988, p. 329.

258 Примечания

15. Сказав это, следует помнить о возможности, указанной в примечании 8 к главе 6, что струны могут иметь значительно больший размер, чем считалось первоначально, и, следовательно, могут стать объектом прямого экспериментального изучения на ускорителях в течение ближайших десятилетий.

16. Для читателя, имеющего математическую подготовку, заметим, что согласно более точной математической формулировке число семейств равно половине абсолютного значения числа Эйлера для пространства Калаби—Яу. Число Эйлера представляет собой сумму размерностей групп гомологий многообразия, где группы гомологии это то, что мы на нашем нестрогом языке назвали многомерными отверстиями. Таким образом, количество семейств, равное трем, следует из того, что число Эйлера для этих пространств Калаби—Яу равно ±6.

17. Интервью с Джоном Шварцем, 23 декабря 1997 г.

18. Для читателя, имеющего математическую подготовку, заметим, что мы ставим в соответствие многообразию Калаби—Яу конечную нетривиальную фундаментальную группу, порядок которой в некоторых случаях определяет знаменатель дробного заряда.

19. Интервью с Эдвардом Виттеном, 4 марта 1998 г.

20. Для читателей, хорошо знакомых с рассматриваемыми вопросами, заметим, что некоторые из этих процессов нарушают закон сохранения лептонного числа, а также СРТ-симметрию (инвариантность относительно изменения знака заряда, четности и направления времени).

Глава 10

1. Отметим для полноты, что хотя большая часть приведенных выше аргументов в равной степени справедлива как для открытых струн (струн со свободными концами), так и для замкнутых струн (которым мы уделяли основное внимание), в рассматриваемом вопросе два типа струн могут, кажется, проявлять различные свойства. Действительно, открытая струна не может быть «насажена» на циклическое измерение. Тем не менее, в результате исследований, сыгравших в конце концов ключевую роль во второй революции суперструн, Джо Польчински из Калифорнийского университета в городе Санта-Барбара и двое его студентов, Джиан-Хюи Дай и Роберт Лей, в 1989 г. продемонстрировали, что открытые струны прекрасно вписываются в схему, которая будет описана в данной главе.

2. Чтобы ответить на вопрос о том, почему возможные энергии однородных колебаний равны целым кратным 1/R, достаточно лишь вспомнить обсуждение квантовой механики (в частности, примера с ангаром) в главе 4. Там мы узнали о том, что согласно квантовой механике энергия, как и деньги, существуют в виде дискретных порций, т. е. в виде целых кратных различных энергетических единиц. В случае однородного колебательного

движения струны во вселенной Садового шланга эта энергетическая единица в точности равна 1/R, как объясняется в основном тексте на основе соотношения неопределенностей. Таким образом, энергия однородных колебаний равна произведению целых чисел на 1 /R.

3. Математически равенство энергий струн во вселенной с радиусом циклического измерения R или 1 /R есть следствие формулы для энергии v/R+wR, где v — колебательное число, а w - топологическое число. Данное уравнение инвариантно относительно одновременных взаимных замен v на w и R на 1/R, т. е. при перестановке колебательных и топологических чисел с одновременной инверсией радиуса. Мы используем планковские единицы, но можно работать и в более привычных единицах, если переписать формулу для энергии через так называемую струнную шкалу 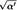, значение которого примерно равно планковской длине, т.е. 10~³³ сантиметра. В результате энергия записывается в виде выражения v/R + wR/', инвариантного относительно взаимной замены v на w и R на  '/R, где последние две величины выражены в стандартных единицах расстояния.

4. У читателя может возникнуть вопрос, каким образом с помощью струны, намотанной вокруг циклического измерения радиусом Я, можно измерить значение радиуса 1/R. Хотя этот вопрос совершенно правомерен, ответ на него, в действительности, заключается в том, что сам вопрос сформулирован некорректно. Когда мы говорим, что струна намотана на окружность радиуса R, мы с необходимостью используем определение расстояния (чтобы фраза «радиус R» имела смысл). Однако это определение расстояния относится к модам ненамотанной струны, т. е. к колебательным модам. С точки зрения этого определения расстояния (и только этого!) конфигурация намотанной струны выглядит так, что струна обернута вокруг циклической компоненты пространства. Однако с точки зрения другого определения расстояния, соответствующего конфигурациям намотанных струн, топологические моды точно так же локализованы в пространстве, как и колебательные моды с точки зрения первого определения, и радиус, который они «видят», равен 1/ R, что и отмечено в тексте.

Эти пояснения дают некоторое представление о том, почему расстояния, измеренные с помощью намотанных и ненамотанных струн, обратно пропорциональны друг другу. Однако, так как данный момент достаточно тонкий, возможно, имеет смысл привести технические подробности для читателя, склонного к математическому образу мышления. В обычной квантовой механике точечных частиц расстояние и импульс (по существу, энергия) связаны преобразованием Фурье. Иными словами, собственный вектор оператора координаты \х) на окружности радиусом R можно определить как 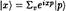, где р = v/R, а \р) есть собственный вектор оператора импульса (прямой аналог того, что мы называли общей колебательной модой струны — движение без изменения формы). В теории струн, однако, есть еще один собственный

Примечания 259

вектор оператора координаты , определяемый состояниями намотанной струны: ,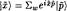

где 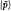— собственный вектор для намотанной струны с . Из этих определений немед-

ленно следует, что х периодична с периодом 2R, а х периодична с периодом 2 /R, так что х есть координата на окружности радиусом R, а — координата на окружности радиусом 1 /R. Более конкретно, можно рассмотреть два волновых пакета 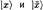, распространяющихся из начала координат и эволюционирующих во времени, с помощью которых можно дать практическое определение расстояния. Радиус окружности, измеренный с помощью каждого из пакетов, будет пропорционален времени возвращения пакета в исходную точку. Так как состояние с энергией Е эволюционирует с фазовым множителем, пропорциональным Et, видно, что время, а, следовательно и радиус, равны t ~ 1 /Е ~ R для колебательных мод и t ~ 1 /Е ~ 1/R для топологических мод.

5. Для читателя, сведущего в математике, отметим, что число семейств колебательных мод струны равно половине абсолютного значения эйлеровой характеристики многообразия Калаби—Яу, как указано в примечании 16 к главе 9. Эта величина равна абсолютному значению разности

где 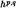обозначает число Ходжа (p,q). С точ-

ностью до константы эти значения равны числу нетривиальных гомологии 3-циклов (трехмерных отверстий) и числу гомологии 2-циклов (двумерных отверстий). Таким образом, хотя в основном содержании говорится о полном числе отверстий, более точный анализ показывает, что число семейств зависит от абсолютного значения разности между числами четномерных и нечетномерных отверстий. Выводы, однако, те же самые. Например, если два пространства Калаби—Яу отличаются перестановкой соответствующих чисел Ходжа и , то число семейств частиц — полное число отверстий — не изменится.

6. Название объясняется тем, что «ромбы Ходжа», математические выражения чисел отверстий различных размерностей для пространств Калаби—Яу, являются зеркальными отражениями друг друга для каждой зеркальной пары.

7. Термин зеркальная симметрия используется в физике и в других контекстах, совершенно не связанных с данным, например, в связи с понятием киральности, т. е. в связи с вопросом о том, является ли Вселенная инвариантной относительно замены правого на левое (см. примечание 7 к главе 8).

Глава 11

1. Для читателя, склонного к математической строгости рассуждений, будет понятно, что вопрос состоит в том, является ли топология пространства динамической, т. е. может ли она меняться во времени. Отметим, что хотя представление о динамических изменениях топологии часто используется в этой книге, на практике обычно рассматривается

однопараметрическое семейство пространственно-временных многообразий, чья топология меняется при изменении параметра семейства. Формально этот параметр не является временем, но в определенном контексте может с ним отождествляться.

2. Для математически подкованного читателя отметим, что процедура включает сдутие рациональных кривых на многообразии Калаби—Яу. Далее используется тот факт, что при определенных условиях образовавшаяся сингулярность может быть устранена серией последовательных раздутий.

3. К. С. Cole, New York Times Magazine, October 18, 1987, p. 20.

Глава 12

1. Цитируется по книге: John D. Barrow, Theories of Everything. New York: Fawcett-Columbine, 1992, p. 13. (В рус. пер. цитата есть в книге: Кузнецов Б. Г. Эйнштейн: Жизнь. Смерть. Бессмертие. М: Наука, 1980, с. 363.)

2. Кратко поясним различия между пятью теориями струн. Для этого отметим, что колебательные возбуждения вдоль струнной петли могут распространяться по часовой стрелке и против нее. Теории струн типов IIА и IIB отличаются тем, что в последней теории колебания в обоих направлениях идентичны, а в первой теории противоположны по форме. Противоположность в данном контексте имеет точный математический смысл, но нагляднее всего ее можно представлять в терминах вращений колебательных мод в каждой теории. В теории типа IIВ оказывается, что все частицы вращаются в одном направлении (у них одна и та же киральность), а в теории типа IIА — в разных направлениях (у них разная киральность). Тем не менее, в каждой теории реализуется суперсимметрия. Две гетеротические теории имеют аналогичные, но более эффектные отличия. Все моды колебаний по часовой стрелке выглядят так же, как и моды струн типа II (если рассматривать только колебания по часовой стрелке, то теории струн типов ПА и IIB идентичны), но колебания против часовой стрелки совпадают с колебаниями исходной теории бозонных струн. Хотя в бозонных струнах возникают неразрешимые проблемы, если рассматривать их колебания в обоих направлениях, в 1985 г. Дэвид Росс, Джеффри Харви, Эмиль Мартинек и Райан Ром (все они в то время работали в Принстонском университете и их прозвали «Принстонский струнный квартет») показали, что при использовании этих струн в комбинации со струнами типа II получается вполне согласованная теория. Однако в этом союзе была странная особенность, известная со времен работ Клода Лавлейса из университета Ратчерса 1971 г. и Ричарда Броуэра из Бостонского университета, Питера Годдарда из Кембриджского университета и Чарльза Торна из Гейнсвилльского университета (штат Флорида) 1972 г. А именно, для

260 Примечания

бозонной струны требовалось 26 пространственно-временных измерений, а для суперструны, как обсуждалось, требовалось 10. Так что гетеротические струны (от греческого 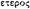, т. е. разный)

являются странными гибридами, в которых колебательные моды против часовой стрелки живут в 26 измерениях, а колебательные моды по часовой стрелке — в 10! Пока читатель окончательно не запутался, пытаясь понять этот странный союз, сообщим ему о работе Гросса и его коллег, в которой было показано, что 16 лишних бозонных измерений должны скручиваться в одно из двух торообразных многообразий очень специального вида, приводя к теориям О- и Е-гетеротических струн. Так как 16 добавочных бозонных измерений компактифицированы, каждая из этих теорий ведет себя так, как если бы в ней было 10 измерений, т.е. как теории струн типа II. В гетеротических теориях также реализован свой вариант суперсимметрии. И, наконец, теория типа I аналогична теории ИВ, за исключением того, что помимо замкнутых струн, рассмотренных в предыдущих главах, в ней имеются струны со свободными концами, называемые открытыми струнами.

Дата добавления: 2014-11-29