
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания по выполнению практических и лабораторных работ
|
|
|
|
Самоконтроль
Чтение учебников
Изучение курса обязательно должно дополняться работой с учебником. Работа с учебником предполагает закрепление основных понятий, формул и рассмотрение дополнительных примеров. Кроме того, в разделе самостоятельная работа рабочей программы указаны конкретные вопросы, подлежащие дополнительную изучению с помощью рекомендованных учебников. При работе с учебником студентам рекомендуется вести дополнительный конспект (помимо лекционного), направленный на закрепление рассмотренного материала.
Результатом изучение определенной темы должно стать усвоение понятий, определений и формул. Студентам рекомендуется осуществлять самоконтроль степени усвоения материала как на формальном, так и на понятийном уровне. Это представляется особенно важным в условиях фактической взаимосвязанности всех тем учебной дисциплины "Теория вероятностей и математическая статистика". В случае трудностей с усвоением материала рекомендуется обратиться за помощью к преподавателю.
| Практические занятия | ||
| № Занятия | Модуль 1 «Теория вероятностей» | Кол.часов |
| Тема «Комбинаторика. Классификация событий. Классическое и статистическое определение вероятности». Размещения, сочетания, перестановки и перестановки с повторениями. Расчет вероятности непосредственно по определению и с применением комбинаторики. Задача о безвозвратной выборке. Решение задач из Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с.: №№ 2.4(а), 2.1, 2.9, 2.10, 2.12, 2.13, 2.15, 2.40, 2.19, 2.20, 2.21, 2.8, 2.16. №№ 3.16, 3.12, 3.18, 3.20, 3.21, 3.22, 3.23, 3.24, 3.25, 3.52. | ||
| Тема «Основные теоремы теории вероятностей». 1) Контроль знаний по теме «Основные понятия и определения теории вероятностей» 2) Решение задач с использованием теорем сложения вероятностей совместных и несовместных событий. Расчет вероятностей для зависимых и независимых событий. Решение задач с использованием теорем умножения вероятностей. Расчет вероятностей для событий зависимых и независимых в совокупности. Решение задач с определением вероятности наступления хотя бы одного из n независимых (зависимых) в совокупности событий. Практика совместного применения теорем сложения и умножения. Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 3.26, 3.33, 3.35, 3.62, 3.54, 3.39, 3.71, 3.72, 3.52, 3.65. Тема «Формулы полной вероятности и Бейеса». Решение задач на применение формул полной вероятности и Бейеса. Обсуждение практики применения формулы Байеса при принятии управленческих решений. Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 4.4, 4.5. Задача-шутка из Мостеллера. | ||
Тема «Случайные величины и их числовые характеристики».
1. Самостоятельная работа по теме «Основные теоремы теории вероятностей»
2. Построение ряда распределения, функции и расчет числовых характеристик дискретных СВ.
Гипергеометрическое распределение рассмотреть на задаче:
На станцию под погрузку поступили 6 вагонов, среди которых 3 предназначены для медикаментов. Случайным образом выбираются 2 вагона. Составьте закон распределения числа вагонов с медикаментами, постройте полигон распределения и найдите числовые характеристики 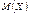 , ,  и и 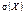 .
Тема «Непрерывные СВ и их числовые характеристики».
Решение задачи: Дана .
Тема «Непрерывные СВ и их числовые характеристики».
Решение задачи: Дана  1) Найти:
1) Найти:  2) Построить графики
2) Построить графики 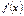 и и 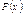 ,
3) Найти ,
3) Найти 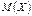 и и  4) Найти
4) Найти 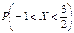
| ||
| Тема «Нормальный закон распределения». Обсуждение особенностей нормального и нормированного нормального распределений. Алгоритмы использования таблиц значений функций нормального закона распределения для определения значений функций нормального распределения с любыми параметрами. Решение задач на расчет вероятности попадания в заданный интервал нормально распределенной случайной величины, вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, правило трех сигм. Решить задачи №№ 6.1, 6.8, 6.9, 6.11-6.13, 6.15 из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с. Тема «Формулы Бернулли и Пуассона». Решить задачу № 5.40 из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с. | ||
| Модуль 2 «Математическая статистика» | ||
Тема: «Вариационный ряд».
Первичная статистическая обработка результатов наблюдений: ранжирование данных, построение вариационных рядов частот и частостей.
Построение интервального вариационного ряда при помощи формулы оптимальной величины интервала.
Построение графиков: полигона, гистограмма, кумуляты и огивы.
Тема: «Числовые характеристики вариационного ряда».
Составляется рабочая таблица для нахождения 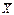 , , 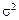 (двумя способами),
находятся среднее квадратическое отклонение и коэффициент вариации. (двумя способами),
находятся среднее квадратическое отклонение и коэффициент вариации.
| ||
Тема: «Статистическое оценивание».
Доверительные интервалы для оценок генеральной средней, генеральной доли при известном и неизвестном 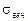 .
Решить задачи №№ 8.60, 8.51 из:
Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с.
Тема: «Статистическая проверка гипотезы».
Проверка гипотезы о значении генеральной средней нормально распределенной генеральной совокупности при известном и неизвестном .
Решить задачи №№ 8.60, 8.51 из:
Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с.
Тема: «Статистическая проверка гипотезы».
Проверка гипотезы о значении генеральной средней нормально распределенной генеральной совокупности при известном и неизвестном 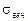 .
Связь доверительного интервала с критической областью. .
Связь доверительного интервала с критической областью.
| ||
| Тема: «Статистическая проверка гипотезы». Проверка гипотез о числовых значениях генеральной доли и генеральной дисперсии. Тема: «Статистическая проверка гипотезы». Проверка гипотезы о равенстве двух дисперсий и двух средних нормально-распределенных генеральных совокупностей. | ||
| Тема: «Статистическая проверка гипотезы». Проверка гипотезы о равенстве двух долей нормально распределенных генеральных совокупностей. Тема: «Статистическая проверка гипотезы». Проверка гипотезы о числовом значении дисперсии генеральной совокупности. | ||
Тема: «Статистическая проверка гипотезы».
Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона 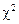 .
Проверка гипотезы о математических ожиданиях нескольких случайных величин методом однофакторного дисперсионного анализа на примере социологического исследования. .
Проверка гипотезы о математических ожиданиях нескольких случайных величин методом однофакторного дисперсионного анализа на примере социологического исследования.
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ
| Темы, задания и рекомендации по самостоятельной работе студентов | |
| Тема «Основные понятия и определения теории вероятностей» Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: глава 4, стр.66-68; §4.2, стр.71-73; §4.1, стр.68-71. Законспектировать самостоятельно: глава 3, §3.1-3.7, стр.57-65 или по Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: стр.58-65, §4.3, стр.73-78. | |
| Тема «Комбинаторика» Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 2.4(а), 2.1, 2.9, 2.10, 2.12, 2.13, 2.15, 2.40, 2.19, 2.20, 2.21, 2.8, 2.16. | |
| Тема «Комбинаторика. Классификация событий. Классическое и статистическое определение вероятности». Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с.: №№ 3.16, 3.12, 3.18, 3.20, 3.21, 3.22, 3.23, 3.24, 3.25, 3.52. | |
| Тема «Основные теоремы теории вероятностей». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: §4.4-§4.5 стр.79-88; §5.1-§5.2, стр.89-95. Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 3.26, 3.33, 3.35, 3.62, 3.54, 3.39, 3.71, 3.72, 3.52, 3.65. | |
| Тема «Формулы полной вероятности и Бейеса». Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: № 3.66 + любые 5 задач из гл.4: №№ 4.1-4.20. | |
Тема «Случайные величины и их числовые характеристики».
Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.:
§6.1-§6.3, стр.100-110, кроме  , §8.2-§8.9.
Самостоятельно: законспектировать §5.3, стр.124-125, разобрать примеры 5.4 и 5.5.
Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.:
пример 5.1, стр.120-121 – разобрать самостоятельно.
Законспектировать гипергеометрическое распределение: §5.6, стр.129-130;
производящая функция: §5.8, стр.132-133.
пример 5.12, стр.133 – разобрать самостоятельно.
Решение задач из:
Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.:
№№ 5.25, 5.26, 5.27, 5.31. , §8.2-§8.9.
Самостоятельно: законспектировать §5.3, стр.124-125, разобрать примеры 5.4 и 5.5.
Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.:
пример 5.1, стр.120-121 – разобрать самостоятельно.
Законспектировать гипергеометрическое распределение: §5.6, стр.129-130;
производящая функция: §5.8, стр.132-133.
пример 5.12, стр.133 – разобрать самостоятельно.
Решение задач из:
Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.:
№№ 5.25, 5.26, 5.27, 5.31.
| |
Тема «Непрерывные СВ и их числовые характеристики».
Решение задачи: Дана 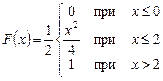 1) Найти:
1) Найти: 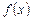 2) Построить графики
2) Построить графики 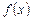 и и  ,
3) Найти ,
3) Найти  и и 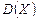 . .
| |
| Тема «Дискретные СВ и их числовые характеристики». Самостоятельно изучить: Равномерное и показательное распределения. Закон больших чисел. Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 9. §9.1-§9.8; глава 7. §7.1-§7.5, стр.123-137. Раздаточный материал. | |
| Тема «Нормальный закон распределения». Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 6.2-6.7, 6.14, 6.19, 6.26, 6.31, 6.32, 6.34, 6.35, 6.33, 6.51, 6.53. | |
| Тема «Формулы Бернулли и Пуассона». Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 5.41-5.43, 5.52, 5.51, 5.80. | |
| Тема: «Вариационный ряд». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 3. §3.1.1-3.1.6; глава 2. §2.1-2.9. Каждый студент выполняет домашнее индивидуальное задание по вариантам. | |
| Тема: «Числовые характеристики вариационного ряда». Каждый студент выполняет домашнее индивидуальное задание по вариантам. | |
| Тема «Выборочный метод и его значение в экономическом анализе». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 11, §11.1-11.5, стр.217-238; глава 13, §13.1, §13,2, §13.4; глава15, стр.225-300. Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: №№ 8.25, 8.30, 8.28, 8.26, 8.17, 8.20, 8.23, 8.48. | |
| Тема: «Статистическая проверка гипотезы». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 16, §16.1, §16.2. Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: примеры 9.2 и 9.3, стр.233-238 – самостоятельно. Ниворожкина Л.И. Статистика. Учебник для бакалавров/ Л.И.Нивороржкина [и др.] под общ. ред. д.э.н., проф. Л.И.Ниворожкиной. – М.:Издательско-торговая корпорация «Дашков и К», 2010, - 416 с.: §8, стр.270-277. | |
| Тема: «Статистическая проверка гипотезы». Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: §9.11, стр.239-242; §9.12, пример 9.6, стр.242-247. | |
| Тема: «Статистическая проверка гипотезы». Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: §9.13-§9.15, стр.248-255. Ниворожкина Л.И. Статистика. Учебник для бакалавров/ Л.И.Ниворожкина [и др.] под общ. ред. д.э.н., проф. Л.И.Ниворожкиной. – М.:Издательско-торговая корпорация «Дашков и К», 2010, - 416 с.: §8.10 и §8.11, стр.291-293. | |
| Тема: «Статистическая проверка гипотезы». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 16, §16.11, стр.339-341; §16.7, стр.325-330. Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: §9.16, пример 9.8, стр.255-258. | |
| Тема: «Статистическая проверка гипотезы». Задачник: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «МарТ», 2005. – 608 с.: §9.12, пример 9.6, стр.242-247. | |
| Тема: «Статистическая проверка гипотезы». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 17, §17, стр.354-360. | |
| Тема: «Статистическая проверка гипотезы». Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.: Глава 17, §11, стр.354-360. |
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 581; Нарушение авторских прав?; Мы поможем в написании вашей работы!