Математические модели процесса получения хлорноватистой кислоты

Проведенные исследования математической модели на устойчивость поливинилхлорида данной марки показали, что положение равновесия системы асимптотически устойчиво.

Полученные результаты кроме теоретического значения имеют и практический характер, так как с их помощью можно более качественно вести технологический процесс полимеризации винилхлорида.

Используя методологию амбивалентных систем, как систем с противоположностями, были получены различные математические модели процесса получения хлорноватистой кислоты. В качестве примера приведем математическую модель процесса получения хлорноватистой кислоты в кислой среде.

Уравнение скорости реакции имеет вид:

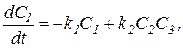
где 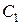- концентрация хлора, 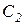- концентрация хлорноватистой кислоты, 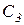- концентрация соляной кислоты, 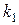- константа скорости прямой реакции, 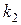- константа скорости обратной реакции.

Так как в любой момент времени хлорноватистая и соляная кислоты образуются в равных концентрациях, то уравнение можно записать в виде:

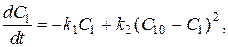
где 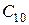- начальная концентрация хлора.

В положении равновесия, когда производная равна нулю, выполняется соотношение:

.

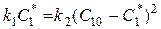Сдвинуть равновесие вправо в направлении образования HOCl можно, выводя из реакции любое из веществ в правой части уравнения. Большинство действующих в промышленности производств получают хлорноватистую кислоту нужной концентрации, связывая соляную кислоту. Добиться этого проще всего прибавлением к реакционной смеси какой-нибудь щелочи. Применяя, например, NaOH, имеем:

HCl + NaOH = NaCl + H₂O.

Процесс получения хлорноватистой кислоты описывается системой четырех нелинейных дифференциальных уравнений первого порядка:

.

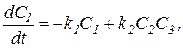
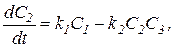
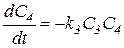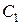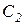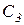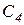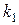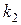В этих обозначениях - концентрация хлора, - концентрация хлорноватистой кислоты, - концентрация соляной кислоты, - концентрация щелочи, и - константы скоростей прямой и обратной реакций в формуле (1), 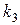- константа скорости реакции.

Константы скоростей отличаются друг от друга на несколько порядков:

, , .

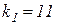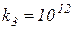Как видно из значений констант скоростей система имеет несколько масштабов времени. Для изучения таких разномасштабных систем широко применяется метод квазистационарных концентраций, который предполагает разделение переменных на два класса: быстрые и медленные и позволяет понизить порядок системы.

Используя принцип выявления противоречия, можно считать, что быстрые и медленные реакции – это и есть противоположности, которые умещаются в одной системе.

Разделим третье и четвертое уравнения системы на больший параметр 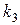и введем обозначения: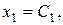

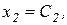
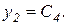
В результате получим систему уравнений с малым параметром при производных:

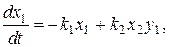
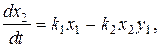
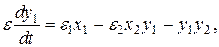
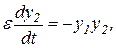
где .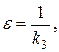

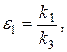
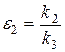Таким образом, система разбилась на две подсистемы. Первые два уравнения системы описывают изменение медленных переменных 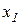и 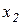, а вторые два уравнения описывают изменение быстрых переменных 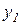и .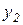

Дата добавления: 2014-12-16