Билет 20. 1. Понятие модели. Информационная модель

1. Понятие модели. Информационная модель. Виды информационных моделей (на примерах). Реализация информационных моделей на компьютере. Пример применения электронной таблицы в качестве инструмента математического моделирования.

Человечество в своей деятельности (научной, образовательной, технологической, художественной) постоянно создает и использует модели окружающего мира.

Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы и др.).

Наглядные модели часто используются в процессе обучения. В курсе географии первые представления о нашей планете Земля мы получаем, изучая ее модель — глобус, в курсе физики изучаем работу двигателя внутреннего сгорания по его модели, в химии при изучении строения вещества используем модели молекул и кристаллических решеток, в биологии изучаем строение человека по анатомическим муляжам и др.

Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т. д. Без предварительного создания чертежа невозможно изготовить даже простую деталь, не говоря уже о сложном механизме.

Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез и пр.), отражающих строение, свойства и поведение реальных объектов.

Все художественное творчество фактически является процессом создания моделей. Более того, практически любое литературное произведение может рассматриваться как модель реальной человеческой жизни. Моделями в художественной форме отражающими реальную действительность, являются также живописные полотна, скульптуры, театральные постановки и пр.

Моделирование — это метод познания, состоящий в создании и исследовании моделей. Каждый объект имеет большое количество различных свойств. В процессе построения модели выделяются главные, наиболее существенные для проводимого исследования свойства.

В процессе исследования аэродинамических качеств модели самолета в аэродинамической трубе важно, чтобы модель имела геометрическое подобие оригинала, но не важен, например, ее цвет. При построении электрических схем — моделей электрических цепей — необходимо учитывать порядок подключения элементов цепи друг к другу, но не важно их геометрическое расположение друг относительно друга и так далее.

Разные науки исследуют объекты и процессы под разными углами зрения и строят различные типы моделей. В физике изучаются процессы взаимодействия и изменения объектов, в химии — их химический состав, в биологии — строение и поведение живых организмов и так далее. Возьмем в качестве примера человека: в разных науках он исследуется в рамках различных моделей. В рамках механики его можно рассматривать как материальную точку, в химии — как объект, состоящий из различных химических веществ, в биологии — как систему, стремящуюся к самосохранению, и так далее.

Модель — это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью. Так, в механике различные материальные тела (от планеты до песчинки) могут рассматриваться как материальные точки, т.е. объекты разные – модель одна.

Никакая модель не может заменить сам объект. Но при решении конкретной задачи, когда нас интересуют определенные свойства изучаемого объекта, модель оказывается полезным, а подчас и единственным инструментом исследования.

Классификация моделей по временному фактору

Статическая модель — это как бы одномоментный срез информации по объекту. Например, обследование учащихся в стоматологической поликлинике дает картину состояния их ротовой полости на данный момент времени: число молочных и постоянных зубов, пломб, дефектов и т.п.

Динамическая модель позволяет увидеть изменения объекта во времени. В примере с поликлиникой карточку школьника, отражающую изменения, происходящие с его зубами за многие годы, можно считать динамической моделью.

При строительстве дома рассчитывают прочность и устойчивость к постоянной нагрузке его фундамента, стен, балок — это статическая модель здания. Но еще надо обеспечить противодействие ветрам, движению грунтовых вод, сейсмическим колебаниям и другим изменяющимся во времени факторам. Это можно решить с помощью динамических моделей.

Предметные и информационные модели

Все модели можно разбить на два больших класса: модели предметные (материальные) и модели информационные.

Предметные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме (глобус, анатомические муляжи, модели кристаллических решеток, макеты зданий и сооружений и др.).

Информационные модели представляют объекты и процессы в образной или знаковой форме.

Образные модели (рисунки, фотографии и др.) представляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кинопленке и др.). Широко используются образные информационные модели в образовании (учебные плакаты по различным предметам) и науках, где требуется классификация объектов по их внешним признакам (в ботанике, биологии, палеонтологии и др.).

Знаковые информационные модели строятся с использованием различных языков (знаковых систем). Знаковая информационная модель может быть представлена в форме текста (например, программы на языке программирования), формулы (например, второго закона Ньютона F = ma), таблицы (например, периодической таблицы элементов Д. И. Менделеева) и так далее.

Иногда при построении знаковых информационных моделей используются одновременно несколько различных языков. Примерами таких моделей могут служить географические карты, графики, диаграммы и пр. Во всех этих моделях используются одновременно как язык графических элементов, так и символьный язык.

Формализация.

На протяжении своей истории человечество использовало различные способы и инструменты для создания информационных моделей. Так, первые информационные модели создавались в форме наскальных рисунков, в настоящее же время информационные модели обычно строятся и исследуются с использованием современных компьютерных технологий.

Процесс построения информационных моделей с помощью формальных языков называется формализацией.

Естественные языки используются для создания описательных информационных моделей. В истории науки известны многочисленные описательные информационные модели. Например, гелиоцентрическая модель мира, которую предложил Коперник, формулировалась следующим образом:

1. Земля вращается вокруг своей оси и вокруг Солнца;

2. орбиты всех планет проходят вокруг Солнца.

С помощью формальных языков строятся формальные информационные модели (математические, логические и др.). Одним из наиболее широко используемых формальных языков является математика. Модели, построенные с использованием математических понятий и формул, называются математическими моделями. Язык математики является совокупностью формальных языков.

Язык алгебры позволяет формализовать функциональные зависимости между величинами. Так, Ньютон формализовал гелиоцентрическую систему мира, открыв законы механики и закон всемирного тяготения и записав их в виде алгебраических функциональных зависимостей. В школьном курсе физики рассматривается много разнообразных функциональных зависимостей, выраженных на языке алгебры, которые представляют собой математические модели изучаемых явлений или процессов.

- матем. запись закона всемирного тяготения

Язык алгебры логики (алгебры высказываний) позволяет строить формальные логические модели. С помощью алгебры высказываний можно формализовать (записать в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Построение логических моделей позволяет решать логические задачи, строить логические модели устройств компьютера (сумматора, триггера) и так далее.

В процессе познания окружающего мира человечество постоянно использует моделирование и формализацию. При изучении нового объекта сначала обычно строится его описательная информационная модель на естественном языке, затем она формализуется, то есть выражается с использованием формальных языков (математики, логики и др.).

Визуализация

В процессе исследования формальных моделей часто производится их визуализация. Для визуализации алгоритмов используются блок-схемы: пространственных соотношений между объектами — чертежи, моделей электрических цепей — электрические схемы, логических моделей устройств — логические схемы и так далее.

Так при визуализации формальных физических моделей с помощью анимации может отображаться динамика процесса, производиться построение графиков изменения физических величин и так далее. Визуальные модели обычно являются интерактивными, то есть исследователь может менять начальные условия и параметры протекания процессов и наблюдать изменения в поведении модели.

Основные этапы разработки и исследования моделей на компьютере

Использование компьютера для исследования информационных моделей различных объектов и систем позволяет изучить их изменения в зависимости от значения тех или иных параметров. Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Часто компьютерные модели проще и удобнее исследовать, они позволяют проводить вычислительные эксперименты, реальная постановка которых затруднена или может дать непредсказуемый результат.

Процесс разработки моделей и их исследования на компьютере можно разделить на несколько основных этапов:

1. Построение описательной информационной модели (выделение существенных параметров).

2. Создание формализованной модели (запись формул).

3. Построение компьютерной модели.

4. Компьютерный эксперимент.

5. Анализ полученных результатов и корректировка исследуемой модели.

На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные с точки зрения целей проводимого исследования параметры объекта, а несущественными параметрами пренебрегает.

На втором этапе создается формализованная модель, то есть описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.

Однако далеко не всегда удается найти формулы явно выражающие искомые величины через исходные данные. В таких случаях используются приближенные математические методы, позволяющие получать результаты с заданной точностью.

На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

1) создание алгоритма решения задачи и его кодирование на одном из языков программирования;

2) формирование компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и т. д.).

В процессе создания компьютерной модели полезно разработать удобный графический интерфейс, который позволит визуализировать формальную модель, а также реализовать интерактивный диалог человека с компьютером на этапе исследования модели.

Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты.

Если компьютерная модель исследуется в приложении, например в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и так далее.

Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности. Например, при построении описательной качественной модели могут быть неправильно отобраны существенные свойства объектов, в процессе формализации могут быть допущены ошибки в формулах и так далее. В этих случаях необходимо провести корректировку модели, причем уточнение модели может проводиться многократно, пока анализ результатов не покажет их соответствие изучаемому объекту.

Исследование математических моделей.

На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы. Точные решения существуют только для некоторых уравнений определенного вида (линейные, квадратные, тригонометрические и др.) поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические, числовые и др.).

Графический метод. Построение графиков функций может использоваться для грубо приближенного решения уравнений. Для не имеющего точного алгебраического решения уравнения вида f(x) = 0, где f(x) — некоторая непрерывная функция, корень (или корни) этого уравнения является точкой (или точками) пересечения графика функции с осью ОХ.

Числовой метод половинного деления. Для решения уравнении с заданной точностью можно применять разработанные в вычислительной математике числовые итерационные методы решения уравнений. Если мы знаем отрезок на котором существует корень, и функция на краях этого отрезка принимает значения разных знаков, то можно использовать метод половинного деления.

Идея метода состоит в выборе точности решения и сведении первоначального отрезка [А;В], на котором существует корень уравнения, к отрезку заданной точности. Процесс сводится к последовательному делению отрезков пополам точкой С = (А+В)/2 и отбрасыванию той половины отрезка ([А;С] или [С;B]), на котором корня нет.

Выбор нужной половины отрезка основывается на проверке знаков значений функции на его краях. Выбирается та половина, на которой произведение значений функции на краях отрицательно, то есть где функция пересекает ось абсцисс.

Процесс продолжается до тех пор, пока длина отрезка не станет меньше удвоенной точности. Деление этого отрезка пополам дает значение корня х = (А+B)/2 с заданной точностью.

Пример. Найти графическим методом корень уравнения 10sin(x)-2x²+5=0.

Формальная модель задана уравнением, для нахождения корня уравнения разработаем компьютерную модель используя электронные таблицы.

Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).

Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.

Приближенное решение уравнения: -0.5 и 2.5.

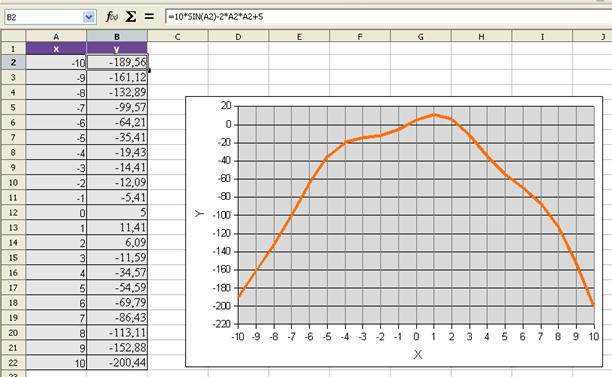
OpenOffice.org Calc

Microsoft Office Excel 2007

Исследование физических моделей

Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол при котором дальность полета будет максимальной.

Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.

1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:

1. тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;

2. изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с² и движение по оси OY можно считать равноускоренным;

3. скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.

2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:

Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:

или

или

3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.

Координата x: =$B$1*COS($B$3*3,14/180)*A6.

Координата y: =$B$2+$B$1*SIN($B$3*3,14/180)*A6-9,8*A6*A6/2.

Визуализируем модель построив график движения тела (зависимость y от x).

4) Исследуем модель и определим искомый угол.

5) Проанализируем полученные результаты.

OpenOffice.org Calc

Microsoft Office Excel 2007

Геоинформационные модели

Геоинформационное моделирование базируется на создании многослойных электронных карт, в которых опорный слой описывает географию определенной территории, а каждый из остальных — один из аспектов состояния этой территории. На географическую карту могут быть выведены различные слои объектов: города, дороги, аэропорты и др.

Широкое распространение получили интерактивные географические карты (мира, различных частей света, России, Москвы и других городов) в Интернете. Такие карты обычно реализуются с использованием векторной графики и поэтому дают возможность пользователю выбирать нужный ему масштаб. Карты связаны с базами данных, которые хранят всю необходимую информацию об объектах, изображенных на картах.

Геоинформационные модели позволяют с помощью географических карт представлять статистическую информацию о различных регионах. Хранящаяся в базах данных информация о количестве населения, развитии промышленности, загрязнении окружающей среды и др. может быть связана с географическими картами и отображена на них. Отображение информации может производиться различными способами: закрашиванием регионов различными цветами, построением диаграмм и так далее.

Например, на сайте http://maps.yandex.ru/ можно сначала выбрать карту (например, Москвы), а затем включить отображение условных обозначений (гостиницы, театры, музеи…).

Во время работы с картой можно менять масштаб (некоторые регионы можно отобразить с точностью до дома).

Можно отобразить не только карту Москвы, но и другого региона...

Дата добавления: 2014-12-16