Главный момент количеств движения системы

Главным моментом количеств движения (или кинетическом моментом) системы относительно данного центра О называется величина 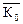, равная геометрической сумме моментов количеств движения всех точек системы относи­тельно этого центра.

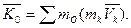
Аналогично определяются моменты количеств движения системы относительно координатных осей:

, , .

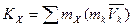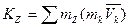При этом 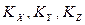представляют собою одновременно проекции вектора 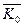на координатные оси.

Подобно тому, как количество движения системы является характеристикой ее поступательного движения, главный момент количеств движения системы является характеристи­кой вращательного движения системы.

Рисунок 25

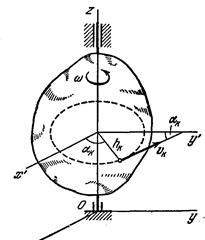
Чтобы уяснить механический смысл величины Ко и иметь необхо­димые формулы для решения задач, вычислим кинетический момент тела, вращающегося вокруг неподвижнойоси (рис.25).Приэтом. как обычно, определение вектора 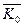сводится к определению его проекций Кх, Ку, Кz.

Найдем сначала наиболее важ­ную для приложений формулу, оп­ределяющую величину Кz, т. е. кине­тический момент вращающегося тела относительно оси вращения.

Для любой точки тела, отстоя­щей от оси вращения на расстоя­нии 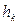, скорость 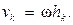Сле­довательно, для этой точки . Тогда для всего тела, вынося общий множитель 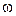за скобку, получим

Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Окончательно находим

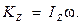
Таким образом, кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

Если система состоит из нескольких тел, вращающихся вокруг одной и той же оси, то, очевидно, будет

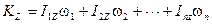
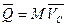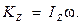Легко видеть аналогию между формулами и : количество движения равно произведению массы (величина, характеризующая инертность тела при поступательном движении) на скорость; кинети­ческий момент равен произведению момента инерции (величина, характеризующая инертность тела при вращательном движении) на угловую скорость.

Теорема об изменении главного момента количеств движения системы (теорема моментов).

Теорема моментов для одной материальной точки будет справедлива для каждой из точек системы. Следовательно, если рассмотреть точку системы с массой 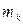, имеющую скорость 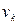, то для нее будет

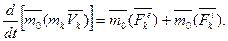
где 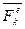и 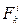- равнодействующие всех внешних и внутренних сил, действующих на данную точку.

Составляя такие уравнения для всех точек системы и складывая их почленно, получим:

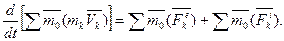
Но последняя сумма по свойству внутренних сил системы равна нулю. Тогда найдем окончательно:

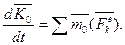
Полученное уравнение выражает следующую теорему моментов для системы: производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра, равна сумме моментов всех внешних сил системы относительно того же центра.

Проектируя обе части равенства на неподвижные оси Охуz, получим:

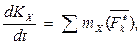
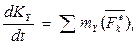
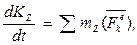
Уравнения выражают теорему моментов относительно любой неподвижной оси.

В кинематике было показано, что движение твердого тела в общем случае сла­гается из поступательного движения вместе с некоторым полюсом и вращательного движения вокруг этого полюса. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изу­чена с помощью теоремы о движении центра масс, а вращатель­ная - с помощью теоремы моментов.

Практическая ценность теоремы моментов состоит еще в том, что она, аналогично теореме об изменении количества движения, по­зволяет при изучении вра­щательного движения системы исключать из рас­смотрения все наперед неиз­вестные внутренние силы.

Дата добавления: 2014-12-17