Модель множественной регрессии

Основные гипотезы

1) Спецификация модели

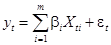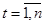, , (1)

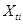– объясняющие (независимые) переменные, 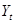– объясняемая (зависимая) переменная, 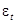– случайное отклонение, 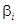– коэффициенты регрессии.

Отметим, что 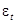и 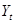– случайные величины, 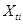может быть как случайной, так и неслучайной (детерминированной) величиной.

Отметим, что уравнение (1) охватывает также случай, когда:

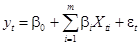(2)

В этом случае можно считать, что

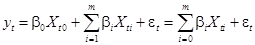, (3)

где .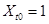

Следовательно, не уменьшая общности, можно считать, что уравнение регрессии задано формулой (1).

Обозначим:

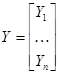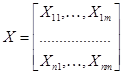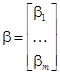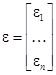, , , (4)

С помощью этих обозначений запишем уравнения регрессии (1) в матричном виде:

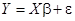(5)

Пример

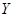
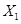
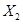
Будем считать, что спецификация модели:

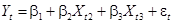
Тогда:

, ,

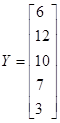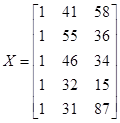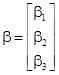
2) 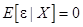(6)

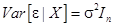3) (7)

Напомним, что 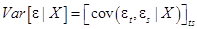– матрица размером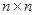

Следовательно, равенство (7) означает, что

т.е. 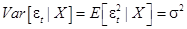, не зависит от (гомоскедастичность);

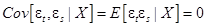при 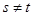– некоррелированность ошибок для разных наблюдений (отсутствие автокорреляции ошибок).

Дополнительная гипотеза:

4) 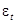– (условно) нормально распределенная случайная величина

Тогда:

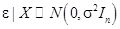(8)

В этом случае модель называется нормальной линейной регрессионной.

Оценка параметров.

Метод наименьших квадратов.

Обозначим:

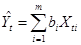(9)

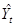– прогнозное значение объясняемой переменной, 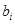– некоторые оценки коэффициентов регрессии .

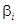Отметим, что 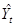зависит от значений коэффициентов .

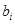Обозначив

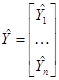, (10)

запишем формулы (2) в матричном виде:

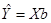(11)

Обозначим:

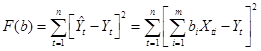(12)

сумму квадратов отклонений прогнозных значений от реальных значений объясняемой переменной.

Метод наименьших квадратов состоит в нахождении таких значени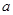й и 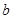, при которых 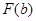минимально:

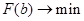. (13)

Запишем необходимые условия экстремума задачи (13):

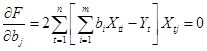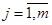, (14)

Систему уравнений (14) приведем к виду:

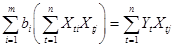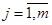, (15)

Запишем эту систему линейных уравнений в матричном виде:

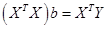(16)

Отметим, что – симметричная квадратная матрица размером .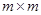

В нашем примере:

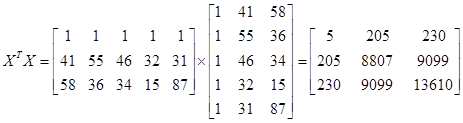
Будем считать, что матрица не вырождена с вероятностью 1:

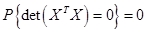(17)

С учетом (17) из (16) имеем:

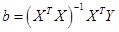. (18)

Формула (18) дает МНК-оценку для вектора коэффициентов регрессии .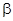

Отметим, что формула (18) обобщает формулы (2.9), (2.10), полученные для случая парной регрессии.

В нашем примере:

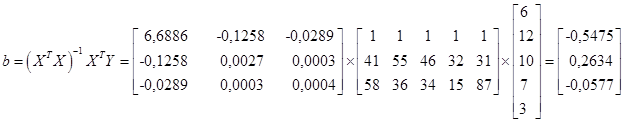
Итак, в нашем примере:

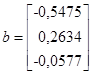
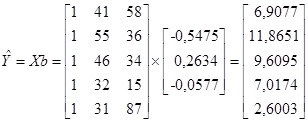
Итак,

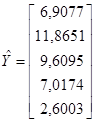
Свойства оценок МНК

Несмещенность

Прежде всего, заметим, что в силу (5) и (6):

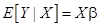. (19)

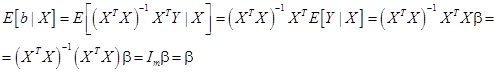
Итак,

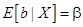. (20)

Следовательно, вектор 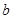является несмещенной оценкой вектора коэффициентов регрессии .

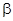Можно также показать, что МНК-оценка 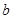является эффективной, т.е. она минимизирует среднеквадратичное отклонение оценки от истинного значения вектора 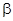: 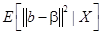, в классе всех несмещенных оценок, линейных по .

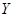Найдем ковариационную матрицу для МНК-оценки .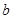

В силу (18) и (5):

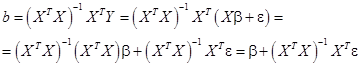
Итак,

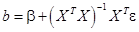(21)

Следовательно,

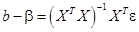(22)

В силу (22) и симметричности матрицы :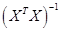

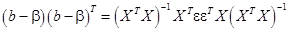(23)

В силу (23) и (7):

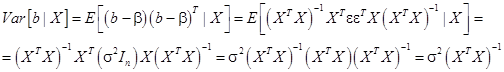
Итак,

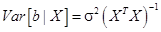(24)

Отметим, что формула (24) обобщает формулы (2.24)-(2.26), полученные для парной регрессии.

Отметим, что в силу (24) 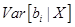– это i -й диагональный элемент матрицы (24).

Обозначив элементы матрицы 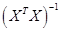через 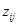, из (24) получим:

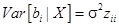. (25)

Обозначим через 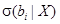стандартное отклонение коэффициента .

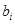В силу (25):

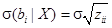(26)

Оценка дисперсии ошибок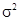

Как и в случае парной регрессии остатки регрессии 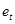определяются из уравнений:

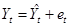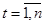, (27)

или, в векторном виде:

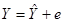(28)

Следовательно,

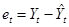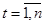, (29)

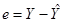(30)

В нашем примере:

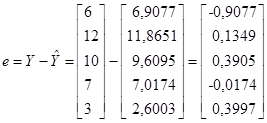
Из (30):

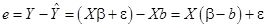
Итак,

(31)

Подставив (21) в (31), получим:

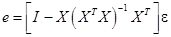(32)

Докажем, что случайные векторы 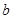и 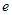независимы.

Для их независимости в силу их нормальной распределенности достаточно доказать их некоррелированность.

В силу (22), (32), (7):

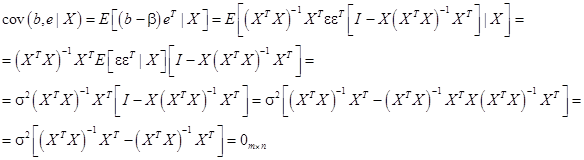
где 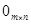– нулевая матрица размера .

Итак,

(33)

В силу (33) векторы 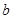и 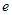не коррелированны, а следовательно и независимы (в силу их нормальной распределенности).

Найдем .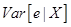

В силу (32), (7):

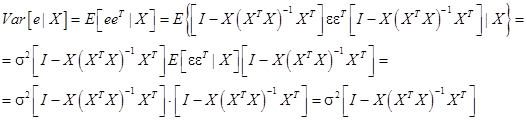
Итак,

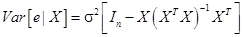(34)

По аналогии со случаем парной регрессии обозначим:

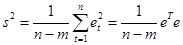(необъясненная дисперсия) (35)

В нашем примере:

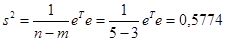
Можно показать, что величина 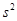является несмещенной оценкой дисперсии ошибок 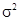, т.е.

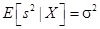. (36)

Отметим, что в силу формулы (35) величина 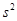является функцией от вектора 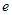. Следовательно, в силу независимости векторов 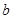и 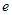вектор 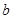и величина 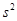также независимы.

Можно показать, что случайная величина 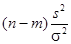имеет распределение «хи квадрат» с числом степеней свободы :

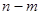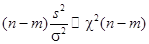(37)

Напомним, что распределение «хи квадрат» с 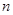степенями свободы – это распределение следующей случайной величины:

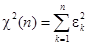(38)

где 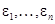– независимые стандартные нормальные случайные величины.

Квадратный корень из 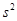называется стандартной ошибкой оценки (стандартной ошибкой регрессии).

В нашем примере:

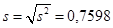
Обозначим:

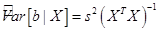, (39)

В силу несмещенности оценки 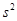из (24) следует, что матрица (39) является несмещенной оценкой ковариационной матрицы векторной МНК-оценки .

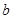В нашем примере:

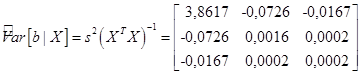
В силу (25) величина

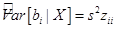(40)

является несмещенной оценкой дисперсии МНК-оценки .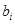

Обозначим:

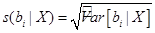(41)

оценку стандартного отклонения .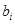

В нашем примере:

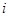
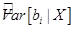
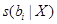
	3,8617	1,9651
	0,0016	0,0397
	0,0002	0,0145

Отметим, что из (40)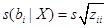, (41):

(41’)

Дата добавления: 2014-12-17