Этап. Отделение корней

Решение

Постановка задачи

ЧИСЛЕНННЫМ МЕТОДАМ

По

Отчеты

Статья 69. Право граждан на обжалование действий государственных органов и должностных лиц, ущемляющих права и свободы граждан в области охраны здоровья

Действия государственных органов и должностных лиц, ущемляющие права и свободы граждан, определенные настоящими Основами, в области охраны здоровья, могут быть обжалованы в вышестоящие государственные органы, вышестоящим должностным лицам или в суд в соответствии с действующим законодательством.

Президент

Российской Федерации

Б.ЕЛЬЦИН

Москва, Дом Советов России

22 июля 1993 года

N 5487-1

Выполнил: студент

гр. 6111-11

Голубев М. С.

Проверила: доцент каф. хим.

кибернетики Кошкина Л.Ю.

Казань, 2012

Содержание

Тема 1. «Численное решение алгебраических. 3

и трансцендентных уравнений». 3

Постановка задачи. 3

Решение. 3

1 этап. Отделение корней. 3

2 этап. Уточнение корней. 4

Листинг программ. 4

Результаты.. 5

Выводы.. 5

Список литературы.. 6

ТЕМА 1. «ЧИСЛЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ

И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ»

Найти корни уравнения f(x) = x³+x-3 с точностью e=0,001. Для решения уравнения используйте следующие методы:

1. метод половинного деления,

2. метод касательных (Ньютона),

3. метод хорд,

4. метод простой итерации.

1. Откроем свой пользовательский файл в табличном процессоре Excel.

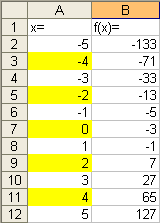
2. Для отделения корней получим таблицу значений аргумента и функции на интервале [1;11]. Для этого в ячейку А1 на Листе 1 введем x=, в В1 введем f(x)=.

3. В ячейку А2 введем -5, далее выполним команды меню Правка – Заполнить – Прогрессия. В появившемся диалоговом окне Прогрессия укажем расположение по столбцам, тип – арифметический, шаг равный 1, предельное значение равное 5.

4.

5. Выделить диапазон ячеек А2:А12 и дать ему имя х, используя команду Вставка – Имя – Присвоить.

6. Введем в ячейку В2 уравнение = f(x) = x³+x-3

7. Скопируем уравнение в ячейки В3:В12.

8. На интервале [1; 3] значение функции меняет знак, т.е. f(a)*f(b)<0. Это и есть

отделенный интервал [a,b], на котором будем уточнять корень заданного уравнения.

1. Для построения графика выделим А1:В12, выполним Вставка – Диаграмма, выберем точечную диаграмму, дадим название осям и диаграмме.

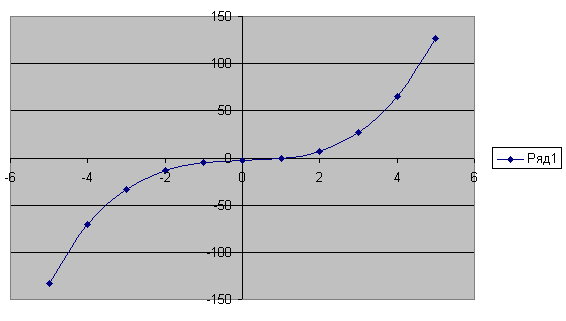
Дата добавления: 2014-12-17