Лабораторная работа №3

Тема: Табулирование функции. Применение табулирования к решению уравнения f(x)= 0.

Цель работы: составление программы табулирования функции y = f(x) и ее использование для нахождения корня уравнения f(x)= 0 с заданной точностью.

Варианты заданий лабораторной работы №3 приведены в таблице 3.1.

Работа состоит из двух задач:

Задача 1. Найти таблицу значений функций y = f(x) на отрезке [ a, b ] с шагом h.

Задача 2. Вычислить корень уравнения f(x) = 0 на отрезке [ a, b ] с точностью e=0,005.

Перед выполнением задания любого уровня необходимо проверить графически, что на заданном отрезке [ a, b ] находится корень уравнения. Если корня на заданном отрезке нет, то следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его. График привести в отчёте.

Задание (1 уровень)

1. Графически получить приближённое решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.

2. Составить блок-схему алгоритма табулирования функции f(x) на отрезке [ a, b ] с шагом h =0,1.

3. Составить программу табулирования функции f(x) на отрезке [ a, b ] с шагом h =0,1.

4. Ввести программу, выполнить её, получить и выписать 11 пар значений (x, y).

5. Для вычисления корня уравнения f(x) = 0 найти и выписать отрезок 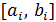, полученный в результатах табулирования, на концах которого f(x) имеет разные знаки.

6. Повторно запуская программу табулирования, получить таблицу значений функции f(x) на отрезке 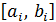с шагом h =0,1.

7. С экрана выписать новый отрезок 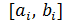, на концах которого функция f(x) имеет разные знаки. Вычислить середину этого отрезка 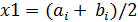– это и будет приближённый корень уравнения f(x)=0, с точностью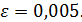

8. Вычислить значение функции в корне. Выписать полученные результаты.

Задание (2 уровень)

1. Графически получить приближенное решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.

2. Изменить блок-схему задачи табулирования функции f(x), предусмотрев возможность повторного запуска алгоритма табулирования на новом интервале с новым шагом h (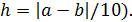 Выход из программы должен быть выполнен, если длина найденного интервала окажется меньше либо равна заданной погрешности e 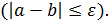Перед выходом вычислить корень уравнения как середину последнего отрезка и значение функции в корне.

3. Составить программу табулирования f(x) на [ a, b ] с шагом h по новой блок-схеме.

4. Запустить программу, получить результаты по табулированию функции f(x) последовательно на данном интервале [ a, b ] с шагом h =0,1 и на каждом новом интервале 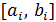, где функция меняет знак на противоположный, с шагом .

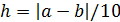5. С экрана выписать результаты табулирования на первом интервале, а для последующих результатов – выписывать две строки, где функция меняет свой знак. Выписать корень уравнения и значение функции в корне.

Задание (3 уровень)

1. Графически получить приближённое решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.

2. Составить блок-схему и программу, реализующие алгоритм вычисления корня уравнения f(x)= 0 на интервале [ a, b ] с заданной точностью 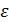. Для нахождения корня использовать алгоритм табулирования функции f(x), последовательно уменьшая в 10 раз интервал поиска 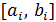, где пока не выполнится условие: .

Замечания:

а) на каждом отрезке 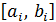проводить не более 10 вычислений значений функции f(x);

б) приближенным решением уравнения считать середину последнего отрезка .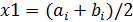

3. Ввести программу, выполнить её и получить результат. На экран вывести границы каждого нового интервала поиска корня, корень уравнения, заданную точность и значение функции в корне.

Пример

Задача 1. Найти таблицу значений функций y = f(x ) на отрезке [ a, b ] с шагом h =0.1, где 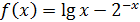, a =1, b =2.

Задача 2. Найти корень уравнения f(x) = 0 на отрезке [ a, b ] с точностью
e= 0.005.

Порядок выполнения задания (1 уровень)

1. Решение уравнения графическим методом.

1.1. Проверим графически, что на заданном отрезке [ a, b ] есть корень уравнения f(x)= 0, т.е.

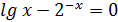. (1)

Перепишем уравнение (1):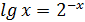

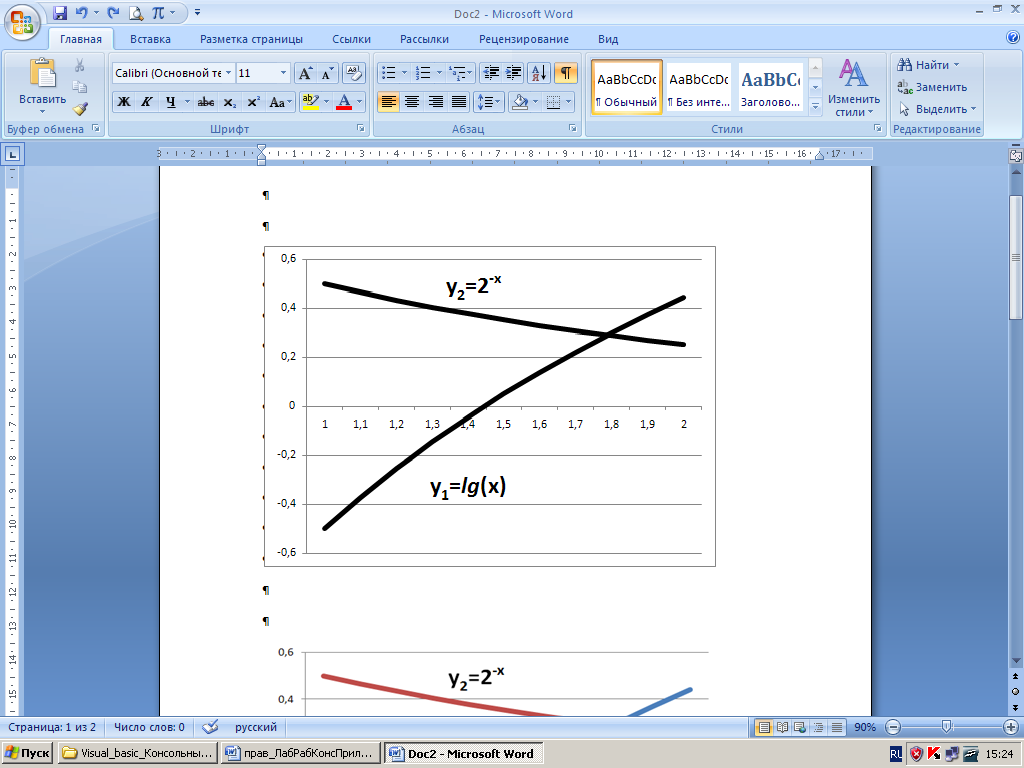
Построим два графика 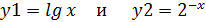(рис. 3.1)

M

X ^*

Рис. 3.1. Пересечение графиков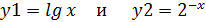

Графики пересекаются друг с другом в точке М. Абсцисса точки М (X^*) – есть корень уравнения

1.2. Если на заданном в условии отрезке графики не пересекаются, то это означает, что данный отрезок не содержит корня уравнения. В этом случае следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его.

2. Составление блок-схемы задачи табулирования.

2.1. Входные данные: a, b – границы отрезка, h - шаг.

Выходные данные: 11 пар значений (x, y).

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAUwHCU8IA AADaAAAADwAAAGRycy9kb3ducmV2LnhtbESPQYvCMBSE7wv7H8Jb8LKsqSKydI1SCqIHYdHV+6N5 tsXkpSTR1n9vhAWPw8x8wyxWgzXiRj60jhVMxhkI4srplmsFx7/11zeIEJE1Gsek4E4BVsv3twXm 2vW8p9sh1iJBOOSooImxy6UMVUMWw9h1xMk7O28xJulrqT32CW6NnGbZXFpsOS002FHZUHU5XK2C 350pvSmp35T30/Z4mhWfu3mh1OhjKH5ARBriK/zf3moFM3heSTdALh8AAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBTAcJTwgAAANoAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA ">

начало

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAZsxCcMIA AADaAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE7wt+h/AEb2uq4LJWo6hQ8SLL+gevj+a1 KTYvpYlav/1mQfA4zMxvmPmys7W4U+srxwpGwwQEce50xaWC0zH7/AbhA7LG2jEpeJKH5aL3McdU uwf/0v0QShEh7FNUYEJoUil9bsiiH7qGOHqFay2GKNtS6hYfEW5rOU6SL2mx4rhgsKGNofx6uFkF m/WlzM7Nz37bmUudVfsim04KpQb9bjUDEagL7/CrvdMKJvB/Jd4AufgDAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBmzEJwwgAAANoAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA ">

a, b, h

x= a,b,h

y=f(x)

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAQCjn8sQA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE70L/w/IK3nRTpa1GV6lCpBcRreL1kX3J BrNvQ3bV9N93C4LHYWa+YebLztbiRq2vHCt4GyYgiHOnKy4VHH+ywQSED8gaa8ek4Jc8LBcvvTmm 2t15T7dDKEWEsE9RgQmhSaX0uSGLfuga4ugVrrUYomxLqVu8R7it5ShJPqTFiuOCwYbWhvLL4WoV rFfnMjs1u+2mM+c6q7ZFNn0vlOq/dl8zEIG68Aw/2t9awfgT/r/EHyAXfwAAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAEAo5/LEAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= ">

a, b, h

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAWip1C8AA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdD/gP4QpuBk11BpFqlFIYdCEM42N/aa5t MbkpScbWvzeLgVkeznuzG6wRD/KhdaxgPstAEFdOt1wruJy/pisQISJrNI5JwZMC7Lajtw3m2vX8 Q49TrEUK4ZCjgibGLpcyVA1ZDDPXESfu5rzFmKCvpfbYp3Br5CLLltJiy6mhwY7Khqr76dcq+D6a 0puS+n35vB4u18/i/bgslJqMh2INItIQ/8V/7oNW8JHGpi/pB8jtCwAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEAWip1C8AAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== ">

конец

2.2. Блок – схема (рис. 3.2):

Рис. 3.2. Блок-схема алгоритма табулирования

3. Составление программы по блок-схеме из п.2.

3.1. Объявить переменные A, B, H, Y, X одинарной точности вещественного типа (Single).

3.2. Запросить ввод исходных данных с клавиатуры (Console.WriteLine()).

3.3. Открыть цикл для вычисления значения функции Y для аргумента X, изменяющегося от A до B с шагом H (For X = A To В Step H).

3.4. В цикле вычислить и вывести на экран значение функции Y(X) и соответствующего аргумента X.

3.5. Закрыть цикл (Next X) и завершить программу.

4. Выполнить программу и выписать результаты в отчёт (по аналогии с рис. 3.3).

x = 1	y = - 0.5	x = 1.6	y = - 0.126
x = 1.1	y = - 0.425	x = 1.7	y = - 0.77
x = 1.2	y = - 0.356	x = 1.8	y = - 0.032
x = 1.3	y = - 0.292	x = 1.9	y = 1.08 E-02
x = 1.4	y = - 0.232	x = 2	y = 5.10 E-02
x = 1.5	y = - 0.177

Рис. 3.3. Результаты: 11 пар значений (x, y)

5. Из таблицы значений, полученной в п.4, найти и выписать отрезок, на котором функция f(x) меняет свой знак. В данном случае это отрезок [ 1.8, 1.9 ], т.к. f(1.8)< 0, а f(1.9)> 0.

6. На найденном отрезке [ 1.8, 1.9 ] запустить программу табулирования функции f(x) с шагом h =0.01.

7. Из полученных результатов найти и выписать две строки, где функция f(x) меняет знак:

x = 1.87 y = - 1.732Е-08 f(x) < 0

x = 1.88 y= 2.474Е-03 f(x) > 0

8. Вычислить середину выбранного отрезка [1.87, 1.88]: X1 =(1.87+1.88)/2 = 1.875 и значение функции в корне X1 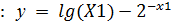(y = 3.743E-04).

9. Выписать результаты: значение корня (X1), значение функции в корне (y(X1)).

Вывод: значение X1 =1.875 является приближённым значением корня уравнения с точностью .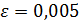

Пояснения к выполнению задания второго уровня

Для реализации выхода из программы выполнить проверку длины найденного отрезка (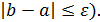 Если это условие не выполняется, то программа должна запросить границы следующего отрезка, на котором функция имеет разные знаки на концах отрезка. Взять границы отрезка с экрана из результатов табулирования на предыдущем отрезке. Если условие выполняется, то необходимо в программе вычислить корень уравнения и значение функции в корне.

Пояснения к выполнению задания третьего уровня

Для поиска в программе нового отрезка табулирования выполнять проверку условия . Для выхода из программы сравнивать длину найденного отрезка с заданной точностью. Перед выходом из программы вычислить корень уравнения и значение функции в корне.

Таблица 3.1. Варианты заданий к лабораторной работе № 3

№ вар.	Уравнение	Отрезок [а, b]	№ вар.	Уравнение	Отрезок [а,b]
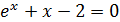
		[0;1]		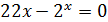	[0;1]
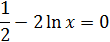
		[1;2]		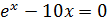	[3;4]
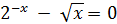
		[0.1;1.1]		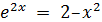	[-1;0]
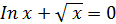
		[0.1;1.1]		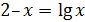	[1;2]
		[2;3]		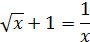	[0.1;1.1]
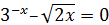
		[0;1]		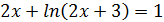	[0;1]
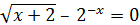
		[-2;-1]		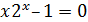	[0;1]
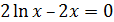
		[0.1;1.1]			[1;2]
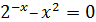
		[0;1]		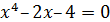	[1;2]
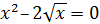
		[-0.5;0.5]		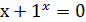	[-1;0]
		[0.1; 1.1]		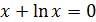	[2;3]
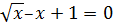
		[0.2;1.2]		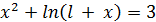	[0;1]
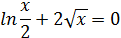
		[0.1; 1,1]		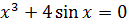	[-0.5; 0.5]
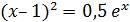
		[0;1]		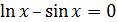	[2; 3]
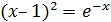
		[1;2]		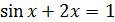	[0;1]

Дата добавления: 2014-12-17