
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные аксиомы статики
|
|
|
|
В статике приняты следующие аксиомы.
Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда силы равны по модулю и направлены по одной и той же прямой в противоположные стороны.
Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему.
Из этих двух аксиом вытекает важное следствие — действие силы на абсолютно твердое тело не изменится, если ее перенести вдоль линии действия в любую другую точку тела. Другими словами, сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор.
Аксиома 3. Равнодействующая двух сил, приложенных к одной точке, равна геометрической (векторной) сумме этих сил и приложена к той же точке.
Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
Аксиома 5 (принцип отвердевания). Равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым.
1.3. Сходящиеся силы и пары сил.
Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Следствием из аксиом 1—3 является возможность приведения системы любого числа сходящихся сил к одной равнодействующей, представляющей векторную сумму всех этих сил. Проекции равнодействующей системы сходящихся сил на оси декартовой системы координат равны алгебраическим суммам проекций этих сил на соответствующие оси. Кроме того, можно показать, что к равнодействующей силе сводится не только система сходящихся сил, но и система, включающая одинаково направленные параллельные силы, и две противоположно направленные параллельные силы с неравными модулями. Две параллельные, равные по модулю, но противоположно направленные силы называются парой сил. Пара сил не имеет равнодействующей; она представляет собой неуравновешенную систему, которая не может быть заменена одной силой.
1.3. Пространственная система сил.
Для описания равновесия в случае произвольной системы сил требуются дополнительные определения.
Моментом 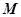 силы
силы  относительно какой-либо точки O (центра) называется векторное произведение радиуса-вектора
относительно какой-либо точки O (центра) называется векторное произведение радиуса-вектора  точки приложения силы относительно точки O на вектор
точки приложения силы относительно точки O на вектор  . Этот момент можно определить и как вектор, численно равный произведению модуля силы на плечо, т.е. на кратчайшее расстояние от точки O до линии действия силы, и направленный перпендикулярно к плоскости, проходящей через указанную точку и линию действия силы в ту строну, откуда “вращение”, совершаемое силой вокруг точки, представляется происходящим против хода часовой стрелки. Такой момент
. Этот момент можно определить и как вектор, численно равный произведению модуля силы на плечо, т.е. на кратчайшее расстояние от точки O до линии действия силы, и направленный перпендикулярно к плоскости, проходящей через указанную точку и линию действия силы в ту строну, откуда “вращение”, совершаемое силой вокруг точки, представляется происходящим против хода часовой стрелки. Такой момент 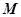 равен нулю тогда и только тогда, когда сила
равен нулю тогда и только тогда, когда сила  и ось лежат в одной плоскости. Момент
и ось лежат в одной плоскости. Момент 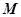 , по определению, является свободным вектором, который может быть перенесен без изменения результата действия в любую точку тела.
, по определению, является свободным вектором, который может быть перенесен без изменения результата действия в любую точку тела.
Проекция этого момента на заданную ось z называется моментом 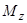 силы относительно оси z. Момент
силы относительно оси z. Момент 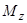 может быть вычислен как момент проекции силы
может быть вычислен как момент проекции силы  на перпендикулярную оси плоскость, который взят относительно точки пересечения оси с плоскостью. Заметим, что проекцией силы
на перпендикулярную оси плоскость, который взят относительно точки пересечения оси с плоскостью. Заметим, что проекцией силы  на плоскость называется вектор, начало и конец которого совпадают с проекциями начала и конца силы
на плоскость называется вектор, начало и конец которого совпадают с проекциями начала и конца силы  на рассматриваемую плоскость. Знак момента
на рассматриваемую плоскость. Знак момента 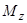 выбирается в соответствии с ранее оговоренным правилом (если наблюдатель видит со стороны положительного направления оси, что проекция силы
выбирается в соответствии с ранее оговоренным правилом (если наблюдатель видит со стороны положительного направления оси, что проекция силы  стремится повернуть тело вокруг рассматриваемой оси против хода часовой стрелки, то берется знак “плюс”, и в противном случае — знак “минус”).
стремится повернуть тело вокруг рассматриваемой оси против хода часовой стрелки, то берется знак “плюс”, и в противном случае — знак “минус”).
Сумма моментов сил, составляющих пару, относительно любой точки, не зависит от положения этой точки и равна моменту пары. В соответствии с приведенными выше определениями можно отметить, что момент пары сил представляет собой вектор, перпендикулярный плоскости пары (плоскости, в которой лежат обе силы), равный по модулю произведению модуля одной из сил на плечо пары (т.е. на кратчайшее расстояние между линиями действия сил пары) и направленный в ту сторону, откуда “вращение пары” видно происходящим против хода часовой стрелки. Момент пары полностью характеризует меру воздействия пары сил на абсолютно твердое тело. Справедливы следующие утверждения:
- две пары, имеющие геометрически равные моменты, эквивалентны; другими словами, пара сил не изменяет оказываемого на абсолютно твердое тело действия при переносе ее в любую принадлежащую телу точку, если плоскость пары переносится параллельно самой себе;
- система нескольких пар приводится к одной паре, момент которой равен векторной сумме моментов всех пар.
Термины «момент», «пара», «плечо» были введены в 1804 г. французским ученым Луи Пуансо (Роinsot, 1777-1859 г.г.).
Пользуясь понятием пары можно сформулировать лемму о параллельном переносе силы: сила, приложенная в какой-либо точке абсолютно твердого тела, эквивалентна системе, состоящей из такой же силы, приложенной в любой другой точке этого тела, и из пары сил, момент которой равен моменту данной силы относительно новой точки приложения (рис. 1.1). Использование этой леммы дает возможность привести произвольную систему сил к некоторой произвольно фиксированной точке О, которая называется центром приведения. Все действующие на тело силы переносятся параллельно в центр приведения. Одновременно прикладываются пары сил, компенсирующие перенос. В результате исходная система сил оказывается за-мененной системой сходящихся в центре приведения сил и пар сил. Последние, допуская перенос, параллельный плоскости пары, могут рассматриваться приложенными также к точке приведения.
В соответствии со следствием из аксиом система сходящихся сил может быть заменена одной равнодействующей, равной векторной сумме всех сил и приложенной в центре приведения. Такая равнодействующая называется главным вектором системы. Все пары сил могут быть геометрически просуммированы. Получающийся в результате момент называется главным моментом системы относительно центра приведения. Численно он равен геометрической сумме моментов всех действующих на тело сил, взятых относительно центра приведения. Таким образом, справедливо следующее утверждение, которое известно как основная теорема статики (теорема Пуансо): всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моментусистемы всех сил относительно центра приведения.
В результате приведения системы сил к некоторому центру получаем так называемые главный вектор и главный момент. Но почему мы здесь используем слово «главный»?
Эти старые термины не совсем хороши, поскольку могут дезориентировать кого-то из студентов. Они возникли в результате неверного перевода французского слова «generate», обозначающего «общий», а вовсе не «главный». Эти термины имеют слишком большой «стаж». Они закрепились в великом множестве изданных книг и стали уже традиционными.
Выше описан закон эквивалентной замены произвольной системы сил простой системой (одной силой и одной парой) на основе геометрического способа (суммирования). Общим способом подобной замены является и аналитический способ. В соответствии с ним проекции главного вектора 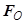 на координатные оси декартовой системы с началом в центре приведения O находятся как суммы проекций
на координатные оси декартовой системы с началом в центре приведения O находятся как суммы проекций  ,
,  и
и 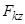 сил
сил  , составляющих исходную систему:
, составляющих исходную систему:
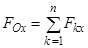 ;
; 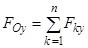 ;
;  ,
,  .
.
Модуль главного вектора 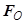 вычисляется по формуле
вычисляется по формуле
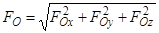 ,
,
а направление определяется направляющими косинусами
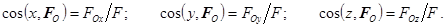
Для вычисления проекций главного момента  имеем
имеем
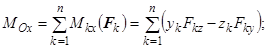

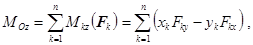
где 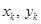 и
и 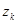 - координаты точки приложения силы
- координаты точки приложения силы 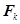 .
.
Модуль 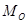 и направляющие косинусы вектора
и направляющие косинусы вектора  равны
равны
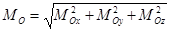 ;
; 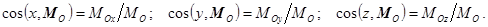
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 955; Нарушение авторских прав?; Мы поможем в написании вашей работы!