Алексей Викторович Иванов

Основное внимание при изучении поверхностей второго порядка следует уделить нахождению линий пересечения поверхностей с плоскостями и выработке навыков построения графиков этих поверхностей по их сечениям плоскостями.

Приведем примеры на эту тему.

Пример 1. Привести к каноническому виду уравнение поверхности второго порядка 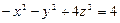. Дать ее название. Найти линии пересечения этой поверхности плоскостями и .

Решение.

1) - каноническое уравнение двуполостного гиперболоида, у которого .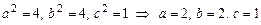

2) Пересечением гиперболоида плоскостью (это – плоскость ) является гипербола .

3) Пересечение гиперболоида плоскостью (это – плоскость, проходящая через точку 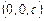параллельно плоскости ) приводит к уравнению 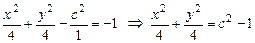. Отсюда видно, что плоскость пересекается с гиперболоидом только при . Линией пересечения служит окружность с центром в точке 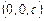и радиусом 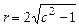. Отметим, что 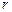растет вместе с ростом . Таким образом, заданный двуполостный гиперболоид является поверхностью вращения вокруг оси .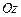

В соответствии с найденными сечениями нетрудно построить приходим график заданной поверхности.

Пример 2. Привести к каноническому виду уравнение поверхности второго порядка 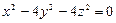. Дать ее название. Найти линии пересечения этой поверхности плоскостям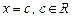и и , и с их помощью построить график этой поверхности.

Решение.

1) - каноническое уравнение конуса с вершиной в начале координат. Ось проходит внутри конуса. .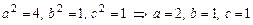

2) Пересечением конуса с плоскостью (это – плоскость ) служит пара прямых: .

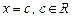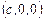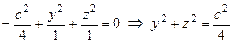3) Пересечение конуса с плоскостью (эта плоскость проходит через точку параллельно плоскости ) дает окружность: с центром в точке 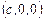и радиусом .

Следовательно, данный конус – конус вращения вокруг оси .

В соответствии с проведенным исследованием строим график этого конуса (рис. 8).

Рис. 8.

_______________________________________________________________________

Домашнее задание.

1. Записать канонические уравнения эллипсоида, однополостного и двуполостного гиперболоидов, конуса, эллиптического и гиперболического параболоидов и привести их графики.

1. Найти линии пересечения поверхности второго порядка координатными плоскостями. Затем, с помощью найденных сечений построить график этой поверхности. Привести название поверхности.

2. Найти линии пересечения поверхности второго порядка 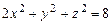координатными плоскостями. Затем, с помощью найденных сечений построить график этой поверхности. Привести название поверхности.

3. Найти линии пересечения поверхности второго порядка 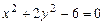плоскостями: ; ; . С помощью найденных сечений построить график этой поверхности. Привести название поверхности.

Дата добавления: 2014-11-29