Уравнение Шредингера для свободной частицы

Уравнение Шредингера

КВАНТОВЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ

Итак, состояние системы описывается волновой функцией Ψ, которая определяется конфигурацией системы и конкретным видом силового поля, в котором она находится. Найти волновую функцию частицы, движущейся в каком либо силовом поле, можно с помощью уравнения относительно этой функции:

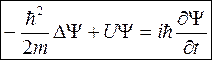(5.1)

где 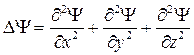– оператор Лапласа, U – потенциальная энергия частицы в конкретном силовом поле (например, энергия электрона в поле притяжения ядра), 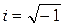мнимая единица, m – масса частицы.

Это уравнение (5.1) в 1926 г. получил Шредингер исходя из аналогии между уравнениями, описывающими ход световых лучей с уравнениями, определяющими траектории частиц в классической механике. Уравнение Шредингера постулируется.

Рассмотрим свободно движущуюся частицу. И если волновой функцией фотона является плоская световая волна, для частиц волновая функция является плоской волной де Бройля, (см. раздел 4).

Для простоты ограничимся одномерным случаем:

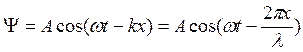(5.2)

Запишем волну де Бройля в комплексной форме:

(5.3)

где частота 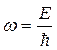, волновое число .

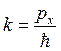Продифференцировав Ψ по времени t, а также дважды по координате x, получим: 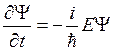, 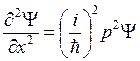(5.4)

Отсюда получаем:

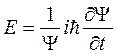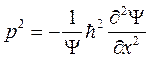, (5.5)

В нерелятивистской классической механике кинетическая энергия E и импульс p связаны соотношением: 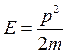(5.6)

Подставив в (5.6) выражения (5.5) и сократив на Ψ, получим уравнение

(5.7)

которое совпадает с (5.1), если в нем U = 0. Отсутствие внешнего силового поля означает, что частица является свободной. Частицу можно считать свободной, если U(x)=const или в общем случае U(r)=const. В этом случае потенциальную энергию можно принять равной нулю.

Дата добавления: 2014-11-29