Особенности расчетов деталей машин на прочность и износостойкость при переменных нагрузках

На практ. зан. 1 было показано, что нагрузка на элементы машин, прежде всего, формируется сопротивлением движению рабочего органа, которое в большинстве случаев во времени не является величиной постоянной. Там же отмечалось, что закон изменения нагрузки может быть установлен аналитически или чаще опытным путем в силу случайности величины сопротивления движению исполнительного механизма. Такую нагрузку принято задавать в виде гистограмм, нагрузочных графиков, циклограмм (рис. 1.6). При расчетах ДМ на прочность, естественно, возникает необходимость ответить на вопрос о назначении величины нагрузки, которая должна быть принята для вычислений в подобных случаях. Как отмечалось выше, в первую очередь из нагрузочного спектра выделяют максимальные кратковременно действующие (пиковые) нагрузки (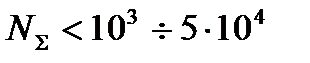), по которым рассчитывают статическую (квазистатическую) прочность элементов машин и которые не учитывают в расчетах на выносливость. Во вторую очередь устанавливают значение нагрузки, которое должно быть принято при расчетах на прочность усталостную.

Существуют два метода расчета: по эквивалентному числу циклов напряжений или по эквивалентной нагрузке (эквивалентным напряжениям). Отметим сущность названных методов на примере расчетов в случае параметризации нагрузки (F, M, T) с помощью ступенчатой циклограммы (рис. 1.6).

Рис. 1.6. Приведение переменной нагрузки к расчетной постоянной в случае расчетов: а – по эквивалентному числу циклов напряжений; б – по эквивалентной нагрузке

Как следует из рисунка, в обоих случаях фактическая переменная нагрузка приводится к эквивалентной (равнозначной) постоянной. Эквивалентность при этом оценивается равнозначным влиянием на усталостную прочность детали, равенством накопленных усталостных разрушений в случае фактической переменной и заменяющей ее постоянной нагрузки. В расчетах по эквивалентному числу циклов напряжений N_E в качестве расчетной нагрузки принимается максимальная длительно действующая сила F₁ (моменты M₁ или T₁) с числом циклов (рис. 1.6 а). Учет того обстоятельства, что за время действия циклов () деталь нагружается большими по сравнению с фактическими нагрузками, компенсируется уменьшением циклов напряжений (N_E ). В соответствии с кривой усталости правомерность такой замены очевидна (см. рис. 1.3). Во–втором методе при расчете по эквивалентной нагрузке за расчетные ее значения принимаются эквивалентная сила F_Е (моменты: изгибающий – М_Е, крутящий – T_Е). Снижение эквивалентной нагрузки по сравнению с максимальной длительно действующей F₁ (M₁, T₁), как это видно из рис. 1.6 б, компенсируется возрастанием значений перечисленных силовых факторов за время действия F₂, M₂, T₂ и последующих ступеней реальной циклограммы.

В основе, вычисления эквивалентного числа циклов напряжений эквивалентной нагрузки лежат уравнение кривой усталости и принцип суммирования повреждений. С физических позиций обозначенный принцип основан на предположении, что на каждом уровне нагрузки детали, конструкции происходят определенные необратимые повреждения П₁, П₂ …П_к, к примеру в виде микротрещин, которые постепенно взаимо независимо нарастают до разрушения детали. В начальный период эксплуатации детали ее суммарное разрушение отсутствует . Опытами установлено, что в качестве меры повреждения на определенном уровне нагрузки можно принять относительную долговечность детали на этой нагрузке

,

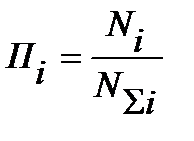где N_i – число циклов напряжений на i ступени нагрузки;

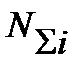- число циклов, необходимое для разрушения детали при этой же нагрузке.

Очевидно, что при достижении (или П_i = 1) деталь вырабатывает свой ресурс и должно произойти ее разрушение. Напомним, что событие разрушения в силу его случайности, строго говоря, следует рассматривать с определенной доле вероятности. Обработка статистических данных по долговечности элементов машин при переменных нагрузках показывает, что операцию суммирования повреждений можно принять линейной

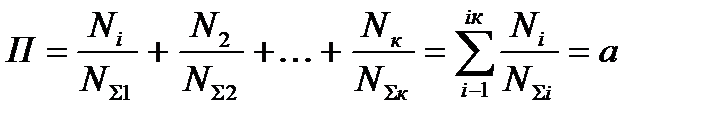(1.31)

Как отмечено выше. при достижении состояния разрушения суммарное повреждение П = 1,0. Однако, в соответствии с опытом в отдельных ситуациях, к примеру при допустимости пластических деформаций П может превосходить единицу (П > 1,0) [1]. По этой причине П в выражении (1.31) обозначено как «а», уточненное значение которого устанавливается опытным путем. Если домножим выражение (1.31) на 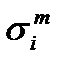, то получим

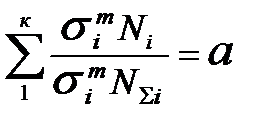(1.32)

Обратим внимание на то обстоятельство, что в знаменателе этого выражения записано уравнение кривой усталости. С физических позиций кривую усталости можно рассматривать как геометрическое место точек, соответствующих факту усталостного разрушения, при определенных значениях напряжений 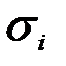и числе циклов 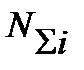можно имитировать напряжениями 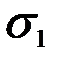(соответствующими максимальной длительно действующей нагрузке F₁, M₁, T₁) при некотором неизвестном числе циклов напряжений N_E, которое можно установить из кривой усталости (рис. 1.7). К такой замене также нередко прибегают при ускоренных испытаниях деталей машин на усталостную прочность.

Рис. 1.7. Имитация разрушения детали при фактическом напряжении и числе циклов 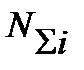с помощью напряжения 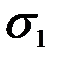при эквивалентном числе циклов напряжения.

Итак, на основе проведенных рассуждений (1) и в силу того, что в знаменателе записана константа, можно заключить

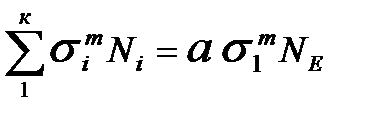
Из этого выражения установим неизвестное эквивалентное число циклов напряжений N_E

(1.33)

Для усредненного значения [1]

(1.34)

Аналогичным путем (1.33) может быть решен для случая имитации разрушения при фактическом напряжени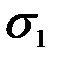и и 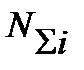некоторым эквивалентным напряжением и фактическом числе циклов напряжений 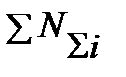или N₀.

Выражением (1.34) удобно воспользоваться в проверочных расчетах при наличии сведений не только о нагрузке, но и о геометрии деталей. Для проектных расчетов, где геометрия изделия должна быть установлена и сведения о напряжениях отсутствуют, целесообразно (1.34) записать через нагрузку. в тех случаях, когда речь идет о напряжениях растяжения, сжатия, изгиба, кручения, в которых напряжения пропорциональны нагрузкам (см. (1.16) … (1.20)), выражение (1.34) можно записать так

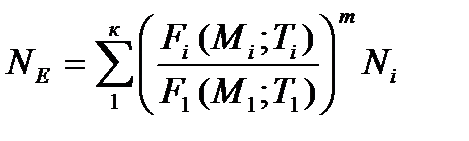(1.35)

В расчетах на контактную выносливость при линейном касании 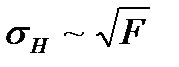(см. 1.23) (1.36)

а при точечном касании 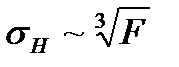, тогда

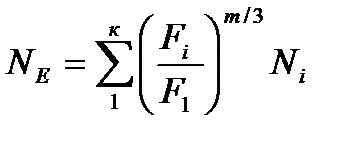(1.37)

Дата добавления: 2014-11-29