Кодування чисел в МП-системах

Вихідні дані, а також проміжні результати в МП-системах можуть бути додатними і від’ємними. Для зображення знаку числа в розрядній сітці перед старшим цифровим розрядом вводиться додатковий знаковий розряд, в який для зображення додатного числа заноситься нуль, а для зображення від’ємного числа – одиниця (див. форму зображення числа з фіксованою крапкою). Для кодування чисел в МП-системах використовують спеціальні коди – прямий, обернений і додатковий.

Прямий код. Зображення двійкового числа Х в прямому коді [ X ]_пр засноване на представленні його абсолютного значення із закодованим знаком.

У загальному випадку формула для утворення прямого коду двійкового числа Х має вигляд

[ X ]_пр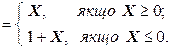

Прямий код [ X ]_пр додатного числа Х в закодованому вигляді повністю співпадає із записом самого числа: якщо Х = + 0. х ₁ х ₂ … х _m , то [ X ]_пр = 0. х ₁ х ₂… х _m.

Прямий код [ X ]_пр від’ємного числа – Х в закодованому вигляді має такий запис: якщо Х = – 0. х ₁ х ₂ … х _m , то [ X ]_пр = 1. х ₁ х ₂… х _m.

Приклади:

Х = +0.11010, [ X ]_пр= 0.11010;

Х = –0.01010, [ X ]_пр= 1.01010.

Відмітимо, що зображення нуля в прямому коді неоднозначне, тобто для тривіальної рівності 0 = + 0 = 0, [+0]_пр =0.00…00; [–0]_пр = 1.00…00. Отже, в прямому коді нуль може мати два уявлення, які відповідно називаються додатнім і від’ємним машинним нулем.

Прямий код використовується в МП-системах для зберігання додатних і від’ємних чисел в запам’ятовуючих пристроях.

Обернений код. Для спрощення структури МП від’ємні дроби, що представлені в двійковій системі числення, кодуються у вигляді доповнень до 2 або до 2–2 ^–m (m – кількість розрядів, 2 – основа двійкової системи числення). Код, утворений доповненням до 2, називається додатковим, а код утворений доповненням до 2–2 ^–m, – оберненим. Обернений код числа Х позначається [ X ]_обр.

Обернений код додатного числа співпадає з його прямим кодом: якщо Х > 0, то [ X ] _обр = [ X ]_пр= Х. Обернений код від’ємного числа утворюється так:

1. в знаковому розряді записується одиниця;

2. в цифрових розрядах одиниці замінюються нулями, а нулі – одиницями.

Приклади:

Х = +0.10110, [ X ] _обр = 0.10110;

Х = –0.01001, [ X ] _обр = 1.10110.

Отже, формула для утворення оберненого коду двійкового числа Х має вигляд

[ X ] _обр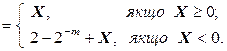

в оберненому коді можливі два уявлення нуля: додатній і від’ємний: [+0]_обр = [+0.00…0]_обр = 0.00…0; [–0]_обр = [–0.00…0]_обр = 10.00…0 – 0.00…01 = =1.11…11.

Спеціальні коди (обернений і додатковий) дозволяють операцію віднімання в МП замінити операцією додавання, що дає можливість зведення всіх арифметичних операцій до виконання операції додавання.

Приклад: скласти числа Х= + 0.101 і Y = – 0.001 в обернених кодах:

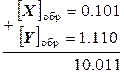
При додаванні кодів одиниця старшого розряду вийшла вліво. В цьому випадку для отримання правильного результату необхідно виконати операцію циклічного переносу. Ця операція полягає в тому, що одиниця, яка вийшла за знаковий розряд, відкидається, а до молодшого розряду числа додається одиниця:

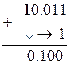
При цьому результат операції додавання додатній, так як в знаковому розряді стоїть 0.

Операція циклічного переносу необхідна тільки тоді, коли одиниця виходить за знаковий розряд. Якщо в знаковому розряді результату стоїть одиниця, то результат операції додавання буде від’ємним.

При використанні цілих чисел формула для утворення оберненого коду має вигляд

[ X ] _обр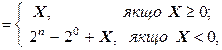

де n – число розрядів.

Додатковий код. Додатковий код додатного числа співпадає з його прямим кодом, тобто [ X ] _дод = [ X ]_пр= Х. Додатковий код від’ємного двійкового числа утворюється так:

1. в знаковому розряді ставиться одиниця;

2. в усіх цифрових розрядах одиниці замінюються нулями, а нулі – одиницями;

3. до молодшого розряду числа додається одиниця.

Приклад:

Х = +0.10010, [ X ] _дод = 0.10010;

Х = –0.0110, [ X ] _дод = 1.1001+0.0001=1.1010;

Х = –0.11001, [ X ] _дод = 1.00110+0.00001=1.00111;

Отже, формула для утворення додаткового коду дробового двійкового числа має вид

[ X ] _дод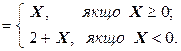

Аналогічним способом можна отримати формулу для утворення додаткового коду цілого двійкового числа:

[ X ] _дод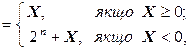

де n – число розрядів.

Для отримання зображення нуля можна виконати такі найпростіші перетворення: [+0]дод = [+0.00 … 0]дод = 0; [–0]дод = [–0.00…0]дод = 10.00…0 + X = 10.00…0 + 0.00…0 = 10.00…0, але в розрядній сітці МП нема розряду ліворуч знакового, тому перша цифра числа МП буде втрачена, а в знаковому розряді залишиться 0. Отже, в додатковому коді нуль в МП має єдине уявлення [+0]дод = [–0]дод = 0.00…0.

При складанні в додатковому коді одиниця переносу, що вийшла за знаковий розряд, відкидається і до молодшого розряду числа не одиниця не додається.

Крапка в цифрових пристроях спеціально не зображується. Місце, де повинна знаходитись крапка, визначається розташуванням цифр по відношенню до уявної крапки.

При складанні чисел в МП можуть отримуватись числа, які по абсолютній величині більше за допустиме значення, що призводить до викривлення результатів обчислень. Тому випадки переповнення розрядної сітки повинні негайно виявлятися. Для цього в МП застосовують спеціальні схеми, що фіксують такі випадки і призупиняють рішення.

Приклад 1:

скласти числа Х= + 0.101 і Y = – 0.001 в додаткових кодах:

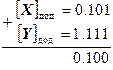
В цьому прикладі виник перенос одиниці (Р ₀ = 1) із знакового розряду, який ігнорується. Крім того, виник перенос одиниці (Р ₁ = 1) із знакового числового розряду в знаковий. Отже, Р ₀ Р ₁ = 0, що свідчить про відсутність переповнення розрядної сітки.

Попередня інформація. Символом позначена логічна операція “додавання за модулем 2”.

Приклад 2:

скласти додатні числа Х = 0.101 і Y = 0.100:

В цьому прикладі Р ₀ = 0; Р ₁ = 1). Отже, Р ₀ Р ₁ = 0 1 = 1, що свідчить про переповнення розрядної сітки.

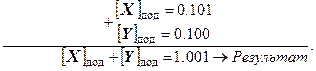
Дата добавления: 2014-11-29