Однорозрядний комбінаційний суматор

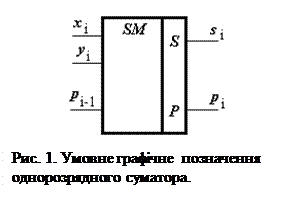Це логічна схема, яка забезпечує отримання сигналів суми та переносу при одночасній подачі кодів слів-доданків. Умовне графічне зображення такого суматора наведене на рис. 1. На входи суматора подаються значення розрядів доданків х _і і у _і та сигнал переносу р _і-1 із сусіднього молодшого розряду. Суматор має два виходи – сума s _i і перенос р _і в старший розряд. Закон функціонування такого двійкового суматора при складанні трьох цифр х _і, у _іі р _і-1 наведено в таблиці 1 для функцій s _i і р _і.

Таблиця 1. Таблиця істинності для функцій s _i і р _і.

Комбінації вхідних сигналів	Вихідні сигнали
х і	у і	р і-1	s i	р і

За цією таблицею можна скласти вирази для перемикаючих функцій:

s _i = ` х <sub>і</sub> ` у _і р _і-1 Ú ` х <sub>і</sub> у <sub>і</sub> `р _і-1 Ú х _і ` у <sub>і</sub> `р _і-1 Ú х _і у _і р _і-1;

р _і = ` х <sub>і</sub> у <sub>і</sub> р <sub>і-1</sub> Ú х <sub>і</sub>` у _і р _і-1 Ú х _і у _і` р _і-1 Ú х _і у _і р _і-1.

Отримані вирази спрощуються, перетворюються за правилами булевої алгебри і визначаються остаточні вирази перемикаючих функцій для їх реалізації на певних логічних елементах. Наприклад:

р _і = ` х <sub>і</sub> у <sub>і</sub> р <sub>і-1</sub> Ú х <sub>і</sub>` у _і р _і-1 Ú х _і у _і` р _і-1 Ú х _і у _і р _і-1 =

= ` х <sub>і</sub> у <sub>і</sub> р <sub>і-1</sub> Ú х <sub>і</sub>` у _і р _і-1 Ú х _і у _і` р _і-1 Ú х _і у _і р _і-1 Ú х _і у _і р _і-1 Ú х _і у _і р _і-1 =

= х _і у _і (р _і-1 Ú ` р <sub>і-1</sub>) Ú х <sub>і</sub> р <sub>і-1</sub> (у <sub>і</sub> Ú у <sub>і</sub> ) Ú у <sub>і</sub> р <sub>і-1</sub>(х <sub>і</sub> Ú` х _і ) =

= х _і у _і Ú х _і р _і-1 Ú у _і р _і-1.

За такими виразами можна побудувати схему для одного розряду комбінаційного суматора.

Рис. 2. Можливі схеми однорозрядного комбінаційного суматора:

а) – суматор на елементах І–АБО; б) – суматор на елементах І–НЕ.

Розглянутий суматор не має пам’яті, і тому після зняття сигналів з входів сигнали суми і переносу на виході також знімаються.

Комбінаційні суматори використовують в тих випадках, коли після того як результат складання з’явиться на виходах комбінаційних схем формування суми, є можливість запам’ятати його в окремому тригерному регістрі.

Швидкодія однорозрядного комбінаційного суматора характеризується часом встановлення вихідних сигналів суми і переносу після встановлення сигналів на входах суматора.

Дата добавления: 2014-11-29