Точность вычисления погрешностей

Как уже говорилось, средняя квадратичная погрешность характеризует реальную ошибку опыта лишь по порядку величины. Поэтому точное вычисление самих погрешностей не имеет особого смысла и при расчетах величины ошибки достаточно ограничиться одной – двумя значащими цифрами. Например, такая запись результатов измерений какой-либо величины: x =2,8674 ±0,0706 бессмысленна. Величину ошибки следует писать либо: Dx= 0,07, либо Dx=0,071.

Поэтому и при записи среднего значения следует ограничиться двумя-тремя цифрами после запятой, округляя до нужных цифр результат: 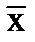=2,87, или 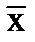=2,867 и окончательный результат записать так:

x=2,87 ±0,07, либо x=2,867 ±0,071.

В данном примере, впрочем, первая запись является более предпочтительной. Дело вот в чем. Давайте оценим относительную погрешность нашего результата:

dx=0,07/2,87=0,025.

Полученный результат означает, что погрешность составляет сотые доли нашего результата. Тем самым, трех значащих цифр достаточно для его записи. Отсюда можно сделать вывод, что количество значащих цифр в результате определяется относительной погрешностью ваших измерений.

Остановимся еще на таком вопросе, – как записывать приближенные значения очень больших или очень малых чисел? Например, мы измерили коэффициент теплового расширения тела a и нашли, что он равен 0,0000163 град^-1, а его относительная погрешность, например, da= 3%. При такой относительной погрешности, как мы видели, следует оставить только три значащих цифры, а их как будто никак не меньше шести. Что делать? Ответ такой – надо записать результат с помощью степеней числа 10, оставив нужное количество значащих цифр:

a=(1,63±0,05)×10^–5 град^-1.

Все расчеты с приближенными числами следует проводить с точностью несколько превосходящей точность измерений, чтобы избежать дополнительных ошибок, связанных с неточностью вычислений. При вычислении обычно сохраняют на один знак больше, чем будет оставлено в окончательном ответе.

Следует при расчете ошибок по формулам (8), (11) или (15) иметь в виду еще одно обстоятельство. Зачастую слагаемые, входящие в правые части этих формул, имеют разные порядки величин. Поскольку расчет ошибок носит, в основном, оценочный характер, то для оценки часто бывает достаточно учитывать в этих формулах лишь те слагаемые, которые имеют наибольший порядок величины, и все остальные слагаемые, малые по сравнению с первыми, просто отбрасывать. Рассмотрим в связи с этим вновь пример определения плотности r. Ошибка Dr дается формулой:

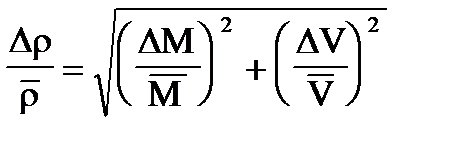
Если при измерении массы тела вы пользовались аналитическими весами, на которых масса тела определяется с точностью до 10^-4 г, а для определения объема измеряли ли­нейные размеры тела, скажем, штангенциркулем, который дает точность до 0,1 мм, то в случае, если М»1-10 г, V»1 см³ получим:

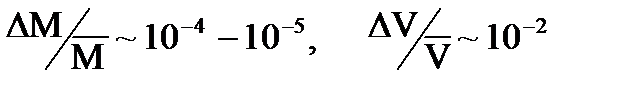
Ясно, что главную роль будет играть погрешность в определении объема, поэтому погрешность в определении массы можно положить равной нулю и полагать:

.

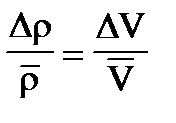Дата добавления: 2014-11-29