Поверочный тепловой расчет

На практике часто возникает необходимость для стандартного или вновь разработанного теплообменника при известных расходах G₁ G₂, начальных температурах t₁’ и t₂’, площади поверхности аппарата F определить конечные значения температур теплоносителей t₁’’ и t₂" или, что то же самое, тепловую мощность аппарата. Из курса тепломассо­обмена [34, 35] известно, что t₁’’ и t₂" можно рассчитать по формулам

; (2.32)

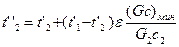, (2.33)

где ε– эффективность теплообменника, определяемая долей его дейст­вительной тепловой мощности от максимально возможной; (Gc) _МИн – наименьшее из G₁c₁ и G₂c₂.

Из курса тепломассообмена и теории теплообменных аппаратов [34, 35, 58] известно также, что в случае прямотока совместное реше­ние уравнений теплопередачи и теплового баланса с учетом уравнения (2.25) дает следующее выражение для эффективности:

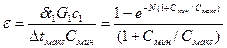, (2.34)

где 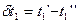; 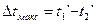, N=kF/C_Min –число единиц перено­са; С_мин, С_макс – наименьшая и наибольшая полные теплоемкости теп­лоносителей, равные соответственно наименьшему и наибольшему про­изведениям расходов теплоносителей на их удельные теплоемкости. В случае противотока

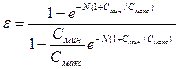. (2.35)

Для перекрестной и более сложных схем движения теплоносителей зависимости ε (N, С_мин/С_макс) приведены в [50, 58].

Если коэффициент теплопередачи заранее неизвестен, его вычисля­ют так же, как при проведении теплового конструктивного расчета.

При С_макс>>С_мин (например, в случае конденсации пара, охлаждае­мого водой)

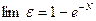, (2.36)

Этим, в частности, можно подтвердить отсутствие влияния на Δt схемы движения теплоносителей при С_макс/С_мин→∞.

Из уравнений: теплопередачи и теплового баланса следует также, что N₁=kF/C_l = δt_l/Δt и N₂=kF/C₂ =δt₂/Δt; ε₁ = δ t₁/Δt_макс и ε₂ = δ t₂/Δt_макс, a ε₁ = ε₂ С₂/C₁. Поэтому по аналогии с формулами (2.34) и (2.35) могут быть получены зависимости вида ε₁ (N₁ C₁ С₂) и ε₂ (N₂ C₁ С₂ ) (см., например, [58]).

Необходимость использовать для каждой конкретной схемы движения теплоносителей свою, отличную от других формулу эффектив­ности затрудняет проведение расчетов. Для устранения отмеченного недостатка можно воспользоваться методом φ-тока, Подробно изло­женным в [58]. В соответствии с этим методом зависимость эффектив­ности ε₂ от числа единиц переноса N₂ и относительной полной тепло­емкости ω=C₂/C₁ для всех без исключения схем движения теплоноси­телей описывается единой формулой

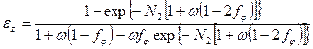, (2.37)

где f_φ, – характеристика схемы тока. Легко видеть, что при f_φ =0 фор­мула (2.37) переходит в формулу (2.34) для прямотока, при f_φ =1– в формулу (2.35) для противотока.

Идея метода φ-тока основана на том, что значения эффективности для подавляющего большинства сложных схем лежат между значения­ми эффективности для прямотока и противотока. Тогда, вводя функ­цию f_φ =0,5(1– cosφ),; при φ=0 получаем f_φ =0, т. е. минимальное значение характеристики схемы тока, которое соответствует прямотоку. При φ=π имеем максимальное значение характеристики f_φ =l, кото­рое отвечает наиболее эффективной противоточной схеме.

Для любой схемы, кроме прямоточной и противоточной, для кото­рой f_φ – величины постоянные, f_φ есть, как правило, некоторая функ­ция от N₂=kF/C₂. Однако расчеты показали, что при, N₂< 1,5 и даже при N₂<=2 f_φ, можно принимать постоянными. Значения этих постоян­ных приведены в табл. 2.3. Там же даны предельные значения харак­теристик схемы тока f_φ *, которые получаются, если в формуле (2.37) осуществить предельный переход при N₂ →∞ и ω→1:

, (2.38)

При использовании уравнения (2.37) появляется возможность про­водить на ЭВМ расчеты теплообменников с различными схемами дви­жения теплоносителей по единообразной методике. При этом любой из теплообменных аппаратов можно представить в виде схемы, содержа­щей параллельно и последовательно включенные элементарные тепло­обменники, в каждом из которых движение теплоносителей носит только либо прямоточный, либо противоточный, либо поперечноточ­ный, либо перекрестно-точный характер, т. е является простым. Раз­меры элементарных теплообменников всегда выбирают достаточно малыми, чтобы можно было пренебречь нелинейным характером изме­нения температуры теплоносителей и рассчитывать средний темпера­турный напор на каждом из элементарных участков поверхности как среднеарифметический.

Таблица 2.3. Характеристики схемы тока и предельной эффективности аппаратов для различных схем движения теплоносителей

Дата добавления: 2014-11-29