Теоретическое введение. Линейная непрерывная математическая модель элемента

Линейная непрерывная математическая модель элемента

Лабораторная работа N№ 1

Моделирование можно рассматривать как последовательный итерационный процесс, в котором выделяются некоторые уровни иерархии.

При математическом моделировании динамических элементов рассматривается иерархическая структура, представленная на рис. 1.

Рис.1. Схема моделирования динамических элементов

При этом используются следующие сокращения: КММ — концептуальная метамодель; ПОЗ — предметная область знаний; НДУ — нелинейное дифференциальное уравнение; ЛДУ — линейное дифференциальное уравнение.

Функционирование динамического элемента можно представить при помощи следующего кортежа на уровне КММ-1:

, (22)

где:		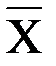—	входной процесс,
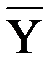
		—	выходной процесс,
	F	—	функция преобразования входного процесса в выходной,
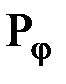
		—	функциональные параметры,
	T	—	время.

В каноническом виде эта запись выглядит так:

. (23)

Входной процесс 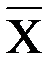, в свою очередь, тоже можно представить при помощи кортежа:

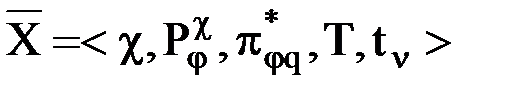, (24)

где:		—	область существования и определения значений вектора-множества ,
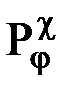
		—	множество функциональных параметров входного процесса,
		—	выделенные параметры,
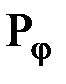
		—	функциональные параметры,
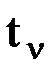
		—	мгновенное значение времени.

Выходной процесс 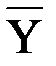можно представить посредством следующего кортежа:

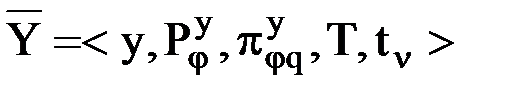, (25)

где:	у	—	область существования и определения значений вектора-множества ,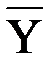
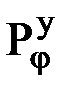
		—	множество функциональных параметров выходного процесса,
		—	выделенные параметры.

Функцию преобразования входного процесса в выходной можно представить таким кортежем:

, (26)

где:		—	конкретизация отображения F,
		—	функциональные параметры,
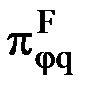
		—	выделенные параметры.

На уровне КММ-2 элементы кортежа уровня КММ-1 конкретизируются и для линейной непрерывной математической модели имеют значения:

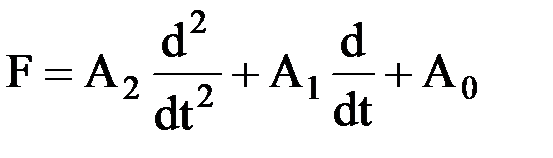, (27)

где F — линейный оператор, такой что F: Y X, где Y, X — линейные пространства непрерывных функций; — множество постоянных параметров.

Также на уровне КММ-2 выделяются интерпретации I:

1. нелинейных дифференциальных уравнений, причем 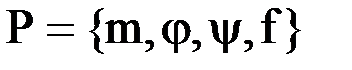— множество переменных параметров;

2. линейных дифференциальных уравнений с запаздыванием, причем F: Y X(t).

От абстрактного математического описания динамического элемента на уровне КММ-2 осуществляется переход к конкретным предметным областям знаний, в качестве которых рассматриваются:

1. биоэлектрическая система (ПОЗ-1);

2. механическая система (ПОЗ-2);

3. электрическая система (ПОЗ-3);

4. экономическая система (ПОЗ-4).

Для предметных областей знаний, удовлетворяющих общему математическому описанию, возможно выделение систем аналогий Аn.

Дата добавления: 2014-11-28