Понятие формальной системы

Появление формальных систем было обусловлено осознанием того факта, что совершенно различные системы, будь то технические, социальные, экономические или биологические, обладают глубоким сходством.

В формальной системе (ФС), оперирующей теми или иными символами, эти символы воспринимаются просто как элементы, с которыми обращаются согласно определенным правилам, зависящим только от формы выражений, образованных из символов. Понятие истинности появляется только в связи с возможными приложениями (интерпретациями) этой системы.

Формальные системы – это аксиоматические системы, т.е. системы с наличием определенного числа исходных заранее выбранных и фиксированных высказываний, называемых аксиомами.

Формальная система считается заданной, если выполнены следующие условия.

1. Задано некоторое множество, состоящее из конечного или бесконечного числа элементов, которые носят название термов. Имеется другое конечное множество, элементы которого есть связки или операции.

2. Любую линейную упорядоченную совокупность термов и операций называют формулой. Из множества формул выделяют подмножеств правильно построенных формул (ППФ). Для ППФ задают правила их конструирования, т.е. определяется эффективная процедура, позволяющая по данному выражению выяснять, является ли оно ППФ в данной ФС.

3. Выделено некоторое множество ППФ, называемых аксиомами ФС. При этом должна иметься эффективная процедура, позволяющая для произвольной ППФ, решить, является ли она аксиомой.

4. Имеется конечное множество отношений между ППФ называемых правилами вывода. Понятие «вывода» также должно быть эффективным, т.е. должна существовать эффективная процедура, позволяющая для произвольной конечной последовательности ППФ решать, можно ли каждый член этой последовательности вывести из одной или нескольких предшествующих ППФ посредством некоторых фиксированных правил вывода. Выводом ФС называется любая последовательность ППФ 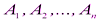такая, что для любого i (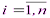) ППФ А_i есть либо аксиома ФС, либо непосредственное следствие каких-либо предыдущих ППФ по одному из правил вывода.

Любая ФС задается четверкой 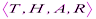, где ^ T – множество термов и операций; H – множество правил конструирования ППФ; A – система аксиом; R – множество правил вывода.

Сама формальная система не является ни языком, ни системой знания, она не содержит никаких утверждений об объектах, а является просто исчислением – некоторого рода действиями по определенным правилам над последовательностями термов.

Два класса формальных систем являются математической базой для построения систем ИИ: исчисление высказываний и исчисление предикатов первого порядка.

Исчисление высказываний как формальная система

Сложное высказывание имеет истинностное значение, которое однозначно определяется истинностными значениями простых высказываний, из которых оно составлено.

Например: «Если студент ложится поздно спать и пьет кофе, то утром он встанет в плохом настроении или с головной болью». Это сложное высказывание состоит из следующих простых высказываний:

«Студент ложиться поздно спать»

«Студент пьет на ночь кофе»

«Утром студент встанет в плохом настроении»

«Утром студент встанет с головной болью»

Обозначив сложное высказывание через ^ X, а простые соответственно через Y, Z, U, V, можно записать

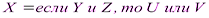
Или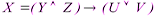

Каждую логическую связку можно рассматривать как операцию, которая образует новое высказывание – сложное из более простых.

Таким образом, всякое сложное высказывание можно записать в виде некоторой формулы, содержащей логические связки и символы, которые обозначают простые высказывания, называемые атомами. Чтобы узнать, истинно или ложно сложное высказывание, достаточно узнать истинные значения всех атомов, из которых оно составлено.

Для формулы состоящей из n атомов существует 2 ⁿ интерпретаций.

Формула исчисления высказываний, которая истинна во всех интерпретациях, называется тавтологией или общезначимой формулой.

Формула исчисления высказываний называется противоречием, если она ложна во всех интерпретациях.

Исчисление предикатов первого порядка

Исчисление высказываний оказывается недостаточным для обоснования, например, таких рассуждений:

«Всякое положительное целое число есть натуральное число. Число 5 есть положительное целое число. Следовательно, 5 есть натуральное число».

Это объясняется тем, что исчисление высказываний ограничивается структурой предложений в терминах простых высказываний, а приведенные рассуждения требуют анализа структуры предложения в смысле связи субъекта и предиката, как это делается в грамматике.

Слово «предикат» имеет два значения. В грамматике – сказуемое, в логике – логическое сказуемое, то, что в суждении высказывается о предмете суждения.

Пусть задано некоторое множество 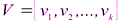, в котором – какие-то определенные предметы из этого множества. Обозначим любой предмет из этого множества через x и назовем x предметной переменной. Тогда высказывания об этих предметах будем обозначать в виде , 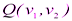и т.д., причем такие высказывания могут быть истинными и ложными. Например, если 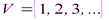, то высказывание «4 есть четное число» является истинным, а «7 есть четное число» – ложным. Если вместо конкретных чисел 4 и 7 поставим предметную переменную x, то получим предикат «x есть четное число», обозначенный P(x).

Таким образом, предикат, который не содержит переменных, совпадает с высказыванием.

Исчисление предикатов первого порядка представляет собой формальную систему, с помощью которой можно выразить большое разнообразие утверждений.

Неотъемлемой функцией языка предикатов является задание слов, которые описывают сущности изучаемого мира, и слов, которые описывают атрибуты, т.е. свойства этих сущностей, их поведение и отношения.

Первый тип слов является термами, второй – предикатами.

Элементарными компонентами языка предикатов являются предикатные символы и символы констант, переменных и функций.

^ Атомарными предикатом называется последовательность из n ( и конечно) термов, заключенная в круглые скобки, которые следуют за предикатным символом. Имя предикатного символа выражено некоторой последовательностью букв.

Например: отец(x, y) – атомарный предикат, описывающий отношение x к y.

В логике предикатов атомарные предикаты задают формулы для описания отношений между сущностями, определяемыми аргументами предикатов.

Если конструктор намеревается описать некоторую предметную область, используя для этого логику предикатов, он может определять предикаты по своему усмотрению в соответствии с конкретной ситуацией. Определение соответствия между элементами языка и отношениями, элементами и функциями в указанной области рассуждения и составляет семантику языка исчисления предикатов.

Очевидно, что определение предиката должно быть однозначным.

Квантер – логические операции, позволяющие перевести одну форму высказывания в другую и указывающие объем переменных, для которых высказывание истинно

Таким образом, исчисление предикатов первого порядка представляет собой расширение исчисления высказываний.

Логический вывод и логическое программирование

Логика – это некоторый способ представления высказываний, создаваемый для того, чтобы, используя формальную процедуру проверить справедливость этих высказываний. Иначе говоря, это наука о способах рассуждений, приводящих к истине. Изучая эти способы логика, интересуется в первую очередь, формой, а не содержанием доводов в том или ином рассуждении. Рассмотрим, например следующие два вывода:

1.
Все люди смертны. Сократ – человек. Следовательно, Сократ смертен.

2.
Все кошки любят молоко. Мурка – кошка. Следовательно, Мурка любит молоко.

Оба вывода имеют одну и ту же форму: все А суть В; С есть А; следовательно С есть В. Истинность или ложность отдельных посылок не является предметом логики. Например, истинность утверждения «все кошки любят молоко» обосновывается значением фактического положения в жизни кошек – это эмпирический факт.

Логический вывод осуществляется из некоторых исходных утверждений с помощью имеющихся схем умозаключений. Используется так же термин «дедукция». Схемы рассуждений принято называть правилами логического вывода.

1.
объявляется некоторый набор фактов, высказываний и отношений между объектами;

2.
определяются правила, которые описывают отношения между объектами;

3.
формируется вопрос об объектах и отношениях между ними.

Вопрос – это средство извлечения информации из логической программы. Правило – общее утверждение об объекте.

Программа объединяет конечное количество фактов и правил. Концепция логического вывода в программировании эквивалентна понятию алгоритма.

Например:

женщина (Алиса)

женщина (Виктория)

мужчина (Эдуард)

мужчина (Джон)

родители (Алиса, Виктория Джон)

родители (Эдуард), Виктория Джон)

сестра (Эдуард, Х)?

Характерным представителем логического программирования является язык ПРОЛОГ.

Дата добавления: 2014-11-29