Действительные числа

К этому моменту математика была уже достаточно развитой наукой. Было решено уже много задач, и, казалось, что рациональных чисел достаточно для решения любой задачи. В Греции ученые успешно занимались геометрией и Евклид, обобщая имеющиеся к этому моменту знания по геометрии, написал свои знаменитые “Начала геометрии”. Вошла туда и известная вам теорема Пифагора. И тут возникло маленькое затруднение. Для формулировки и доказательства своей теоремы Пифагор использовал возведение в степень и извлечение корня. Возведение в степень было определено как произведение нескольких одинаковых сомножителей , а затем ввели обратное ему действие - извлечение корня. И стали выяснять, чему равно число . Точнее говоря, какому рациональному числу равно число . И неожиданно выяснили, что никакому. То есть что не является рациональным числом. Доказательство этого факта приведем полностью, потому что оно очень характерно для математики.

Доказательство.

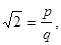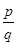Пусть где - число целое, - число натуральное, а - несократимая дробь. Возведем обе части равенства в квадрат , и приведем к общему знаменателю Это равенство означает, что четное число. Но квадрат целого числа может быть четным только если само число четное, то есть для некоторого целого . Подставляя значение в предыдущее равенство, получим . Разделим обе части равенства на 2. Получим . Значит 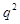, а следовательно и четные числа. То есть для некоторого целого . Но тогда , то есть исходную дробь можно сократить, что противоречит предположению, и, значит, число не является рациональным числом. Это был шок. Это означало, что существуют еще какие-то числа помимо рациональных. Их назвали иррациональными. Иррациональное число - это число, которое записывается бесконечной десятичной непериодической дробью.

Иррациональные числа вместе с рациональными образуют множество действительных чисел, которое обозначается буквой R.

Дата добавления: 2014-11-28