Метод контурных токов

Метод позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Кирхгофа.

Рассмотрим электрическую цепь (рис.1.18), в которой выберем три независимых контура. Контуры образованы собственными контурными ветвями и общими ветвями контуров. Направления токов и ЭДС в ветвях указаны произвольно, кроме того, заданы параметры сопротивлений и ЭДС в ветвях. Необходимо определить токи ветвей. В независимых контурах произвольно выберем направления контурных токов и ЭДС, которые обозначим по номеру контура с одинаковыми двойными индексами номеров контуров.

Пусть направления контурных токов и ЭДС совпадают с направлениями токов и ЭДС собственных контурных ветвей и значения этих токов равны, т.е.

Токи в общих ветвях контуров определяются по первому закону Кирхгофа:

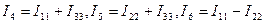
Рис.1.18. Электрическая схема с тремя независимыми контурами

Контурные ЭДС равны алгебраической сумме ЭДС ветвей, входящих в каждый независимый контур:

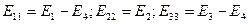
Арифметические суммы сопротивлений всех резистивных элементов, входящих в каждый из выбранных контуров, называются собственными контурными сопротивлениями, и обозначаются двойными индексами номеров контуров:

Сопротивления резистивных элементов, находящихся в общих ветвях двух контуров, называются общими сопротивлениями этих контуров:

Для определения контурных токов составим систему контурных уравнений по второму закону Кирхгофа для рассматриваемой электрической цепи, у которой три независимых контура:

(1.54)

Подставим в значения собственных и контурных сопротивлений резистивных элементов ветвей, а также в значения контурных ЭДС ветвей цепи, систему уравнений (1.54) преобразуем:

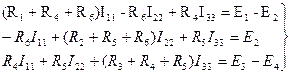(1.55)

Систему уравнений (1.55) представим в матричной форме

AIR = E, (1.56)

где АR - квадратная матрица 3х3 постоянных коэффициентов значений сопротивлений при контурных токах цепи, I - вектор-столбец неизвестных контурных токов, Е - вектор-столбец постоянных коэффициентов значений контурных ЭДС цепи.

Преобразуем систему уравнений (1.56)

I = AR ֿ ¹E. (1.57)

Система уравнений (1.57) в раскрытой матричной форме будет иметь вид:

В среде MATLAB выражение (1.57) будет иметь вид:

I = inv (AR)*E, (1.58)

где inv(AR) - инверсия матрицы АR; E - вектор - столбец значений ЭДС цепи.

После подстановки значений сопротивлений и ЭДС ветвей цепи, компьютер выдаст численное решение неизвестных значений контурных токов цепи: 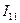, , 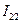, 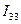по которым легко определяются значения токов ветвей цепи.

1.10. Работа и мощность постоянного тока. Закон Джоуля – Ленца

Источник электрической энергии совершает полезную работу в замкнутой электрической цепи, при этом возникает электрический ток. Работа источника связана с перемещением электрического заряда Q и зависит от ЭДС:

A = E∙Q. (1.59)

Так как Q = I∙ t, E = U+UBT, то A = (U+UBT)I∙t или A = U∙I∙t + UBТ ∙I∙t,

где U∙I∙t = А - работа, совершаемая источником на внешнем участке цепи,

UBТ ∙I∙t = АBT - потери энергии внутри источника.

Используя закон Ома для участка цепи, можно записать:

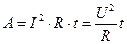. (1.60)

Мощностью источника постоянного тока называют работу источника, совершаемую за единицу времени:

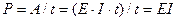. (1.61)

Мощность потребителей:

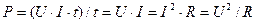. (1.62)

Мощность потерь энергии внутри источника:

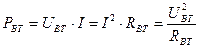. (1.63)

Единица мощности - ватт (Вт):

.

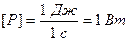Единица электрической работы - джоуль (Дж):

.

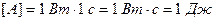На практике пользуются единицей мощности киловатт (кВт): 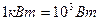и единицей работы (киловатт-час): .

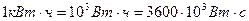При прохождении тока по проводнику свободные электроны, перемещаясь под действием поля, сталкиваются с ионами кристаллической решетки проводника. При этом кинетическая энергия электронов передается ионам, увеличивая при этом их амплитуду колебания, что приводит к нагреванию проводника. Количество теплоты, выделяемой в проводнике при прохождении тока, пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока, и носит название закона Джоуля - Ленца:

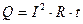[Дж]. (1.64)

Преобразование электрической энергии в тепловую энергию имеет большое практическое значение и широко используется в нагревательных приборах, в устройствах электрического освещения. Однако часто тепловые потери являются нежелательными, например, в электрических машинах, трансформаторах и других устройствах, что снижает их КПД. Во избежание перегрева проводов, обмоток электрических машин, электрических аппаратов установлены нормы допустимого значения силы тока и сечений проводников, которые приводятся в Правилах устройства электрических установок.

Например, необходимо рассчитать сечение провода на допустимый ток. Если расстояние между источником электрической энергии и потребителем [ м ], то длина двух проводов - 2 [ м ]. Сопротивление проводов сечением S [ м ²] с удельным сопротивлением 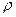[ Ом · м ] равно: 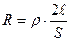. Падение напряжения на проводах 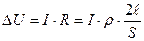, тогда сечение проводов 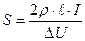. Найденное сечение проводов округляют до большего стандартного ближайшего значения.

Для защиты электрических аппаратов, машин и приборов от больших токов используются предохранители и автоматы.

При расчете параметров электрических цепей необходимо соблюдать баланс мощностей: алгебраическая сумма мощностей всех источников энергии электрической цепи равна арифметической сумме мощностей всех приемников энергии:

. (1.65)

Дата добавления: 2014-11-29