Множества

Теория множеств как математическая дисциплина создана немецким математиком Г.Кантором (1845-1918).

Множество – одно из основных (фундаментальных) понятий математики, а потому строгого определения не имеет. Описательно термин «множество» объясняется как собрание, совокупность, набор некоторых объектов произвольной природы, объединенных по каким-то общим для них признакам. Объекты, из которых состоит множество, называют его элементами.

Примеры множеств: все студенты университета, собрание книг в библиотеке, множество звезд Солнечной галактики, множество целых чисел и т.д.

Исходя из примеров, можно определить свойства множества:

1) элементы множества должны быть строго определены;

2) каждый элемент должен учитываться только один раз;

3) порядок расположения элементов внутри множества не имеет значения.

Пример: Множество студентов какой-либо группы университета.

Понятно, принадлежит студент данной группе или нет, в ведомости каждый учитывается только раз и порядок расположения фамилий не имеет значения.

Множества обозначают заглавными буквами латинского алфавита: A, B, C, D...; элементы – строчными: a, b, c,...

Символическая запись 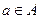означает принадлежность элемента a множеству А. Запись 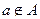означает, что элемент а не принадлежит множеству А.

Пример: Пусть А – множество четных чисел. Тогда , а .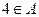

Если число элементов множества конечно, то множество называют конечным, иначе – бесконечным. Считается, что примеры множеств, взятых из материального мира, конечны. Числовые множества – бесконечны.

Пример: Множество рыб в океане велико, но конечно. Множество действительных чисел – бесконечно.

Множество, не содержащее ни одного элемента, называется пустым и обозначается символом .

Существуют разные способы задания множеств. Конечное множество можно задать перечислением его элементов.

Пример: С= 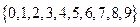-- множество цифр десятичной системы счисления.

Также задать множество можно с помощью характеристического признака.

Пример: 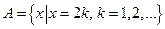-- множество четных чисел.

Два множества равны, когда они состоят из одних и тех же элементов.

Пример: Множества 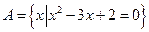и равны.

Пример: Множества 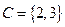и равны.

Множество А называют подмножеством множества В, если каждый элемент множества А является одновременно элементом множества В. В этом случае пишут (читается: «А включается или содержится в В»). Любое множество содержит в качестве подмножества. Очевидно, 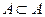(записывают 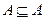); А и называют несобственными подмножествами множества А. Все остальные подмножества называют собственными, т.е. кроме его элементов в множестве должен содержаться еще хотя бы один элемент.

Пример: Пусть 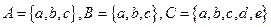, тогда .

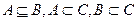Основные свойства включения: если ;

если 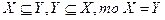-- равные множества.

Если все рассматриваемые множества, в ходе какого-либо рассуждения, являются подмножествами некоторого множества U, то это множество называют универсальным.

Пример: R – множество действительных чисел – универсальное множество, если в процессе изучения рассматриваются множества натуральных, целых и рациональных чисел

Существуют следующие операции над множествами:

1) объединение: 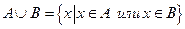-- элементы нового множества лежат хотя бы в одном из множеств А или В;

2) пересечение: -- элементы нового множества лежат в обоих множествах А; В;

3) разность: 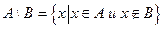-- элементы нового множества – это элементы множества А, не содержащиеся в В;

4) дополнение множества А в множестве U (): .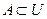

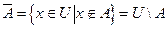Пример: .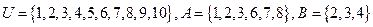

Тогда .

Введенные операции обладают следующими свойствами:

(коммутативность).

(ассоциативность).

(дистрибутивность)

(идемпотентность).

(поглощение).

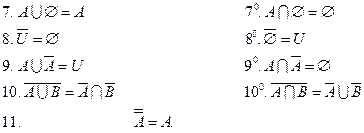
Задачи.

1. Используя диаграмму Венна, доказать законы 3 и 5.

2. Используя законы множеств, доказать равенства:

a) .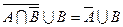

b) .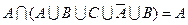

c) .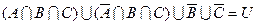

3. Заданы множества 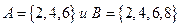. Верным для них будет утверждение...

Варианты ответов:

a) «Множества А и В равны».

b) «Множество B есть подмножество множества A».

c) «Множество А есть подмножество множества В».

d) «Множества А и В не содержат одинаковых элементов».

4. Заданы произвольные множества А, В и С. Расположить указанные ниже четыре множества так, чтобы каждое из них было подмножеством следующего за ним:

a)

b)

c)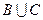

d) .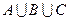

5. Даны множества . Установить соответствия между следующими множествами и их элементами:

6. Принято обозначать:

N – множество натуральных чисел;

Q – множество рациональных чисел;

Z – множество целых чисел;

R – множество действительных чисел.

Тогда верным утверждением будет...

Варианты ответов:

7. С помощью диаграмм Венна исследовать вопрос о справедливости каждого из следующих рассуждений:

а) если А, В, и С – такие подмножества множества U, что

;

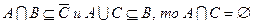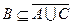b) если А, В, и С – такие подмножества множества U, что и , то .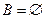

Дата добавления: 2014-11-29