М. Донецк , ул. Артема, 118-б

Задача определения максимального потока.

Рассматривается сеть с одним узлом входа (источник) и одним узлом выхода (сток). Какова максимальная величина потока (количество машин, сообщений, жидкости и т.д.), который может войти в сетевую систему и выйти из нее в заданный период времени? При этом предполагаем, что поток, вытекающий из узла, равен потоку, втекающему в узел.

Под пропускной способностью (мощностью) дуги будем понимать верхнее ограничение на поток в этой дуге. Мощность потока может зависеть от его направления. Условное изображение в сети

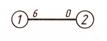
Означает, что мощность потока от узла 1 к узлу 2 равна 6, а мощность от 2 к 1 равна 0.

Алгоритм определения максимального потока:

1. Найти какой-либо путь от источника до стока, который образован дугами, каждая из которых имеет в направлении потока ненулевую мощность. Если такого пути нет, то оптимальное решение найдено.
2. Найти наименьшее значение мощности дуги Р на выбранном пути шага 1. Увеличить поток через сеть на величину Р.
3. На пути из шага 1 сократить на Р мощности потоков на всех дугах в направлении потока и увеличить на Р мощности потоков на всех дугах в обратном направлении. Перейти к шагу 1.

Пример. Система автодорог «Север-Юг», проходящих через Псковскую область, может обеспечить пропускные способности, показанные на приводимой ниже схеме (тыс. автомашин в час).

Каков максимальный поток через эту систему (тыс. автомашин в час)? Сколько автомашин должно проехать по дороге 5-6, чтобы обеспечить максимальный поток?

Искомую величину максимального потока положим равной нулю.

Выбираем путь 1-3-6. Р=min(6,2)=2. Поэтому мощности потоков на пути 1-3-6 в направлении потока уменьшаем на величину Р=2, а мощности потоков в обратном направлении на пути 1-3-6 увеличим на Р=2. Общий поток станет 0+2=2. Получим:

Выбираем путь 1-4-6. Р=min(3,3)=3. Все потоки на пути 1-4-6 в направлении общего потока уменьшаем на 3, а в обратном направлении увеличиваем на 3. Общий поток увеличиваем на 3. Итого, 2+3=5. Получим:

Выбираем путь 1-2-5-6. Р=min(2,4,6)=2. Все потоки на пути 1-2-5-6 в направлении общего потока уменьшаем на 2, в обратном увеличиваем на 2. Общий поток увеличиваем тоже на 2. Итого 5+2=7. Получим:

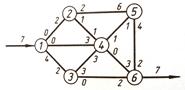
Выбираем путь 1-3-4-5-6. Р=min(4,3,1,4)=1. Все потоки на пути 1-3-4-5-6 в направлении общего потока (4,3,1,4) уменьшаем на величину Р=1, а все потоки на этом пути в обратном направлении увеличиваем на Р=1. Итого, общий поток 7+1=8. Получим:

Выбираем путь 1-3-4-2-5-6. Р=min(3,2,1,2,3)=1. В прямом направлении уменьшаем на 1, в обратном увеличиваем на 1. Общий поток равен 8+1=9. Получим:

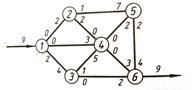
Больше не существует путей из узла 1 в узел 6 с мощностью, превышающей 0 на всем пути (Р=0). Следовательно, 9 тыс. – это максимальный поток через сеть.

Определим теперь величину и направление потока на каждой дуге, чтобы достичь максимального потока в 9 тыс. автомобилей. Поток проходит по дуге с величиной, равной разнице между первоначальной и конечной мощностями потока. Так, первоначальная мощность дуги 1-2 равна 2, а конечная – 0. Тогда в направлении от узла 1 к узлу 2 поток имеет мощность 2-0=2. Сравнивая конечные и начальные мощности потока для всех дуг сети, мы получаем конечную модель потоков.

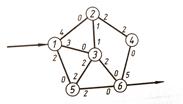
Задача.

Чему равен максимальный поток автомашин для системы автодорог? Рассматривается возможность введения секции 3-4 с пропускной способностью 3 тыс. автомашин в час. На сколько увеличится величина максимального потока автомашин?

Литература

Просветов Г.И. Дискретная математика: задачи и решения. – М.: БИНОМ. Лаборатория знаний, 2011.

Канцедал С.А. Дискретная математика: учеб. Пособие. – М.:ИД «ФОРУМ»: ИНФРА-М, 2011.

Стол Р.Р. Множества. Логика. Аксиоматические теории. – М.: Просвещение, 1968.

Андерсон Дж. А. Дискретная математика и комбинаторика. – М.: Вильямс, 2003.

Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика. – Ростов н/Д: Феникс, Харьков: Торсинг, 2003.

Дата добавления: 2014-11-29