
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоретические положения. Цель работы: исследование симметричных и несимметричных режимов работы трехфазной цепи при соединении потребителей «звездой»
|
|
|
|
Лабораторная работа №7
ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ ПОТРЕБИТЕЛЕЙ «ЗВЕЗДОЙ»
Цель работы: исследование симметричных и несимметричных режимов работы трехфазной цепи при соединении потребителей «звездой», выявление роли нулевого провода.
Трехфазная система переменного тока представляет собой совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты и амплитуды, но сдвинутые по фазе относительно друг друга на  . Каждую отдельную цепь принято называть фазой. При соединении «звездой» концы фаз соединяются в одну точку, называемую нулевой точкой (или нейтралью), к которой может быть подведен четвертый провод схемы, называемый нулевым (нейтральным) проводом. На рис. 1. изображена схема трехфазной системы с нулевым проводом, так называемая «четырехпроводная» схема.
. Каждую отдельную цепь принято называть фазой. При соединении «звездой» концы фаз соединяются в одну точку, называемую нулевой точкой (или нейтралью), к которой может быть подведен четвертый провод схемы, называемый нулевым (нейтральным) проводом. На рис. 1. изображена схема трехфазной системы с нулевым проводом, так называемая «четырехпроводная» схема.
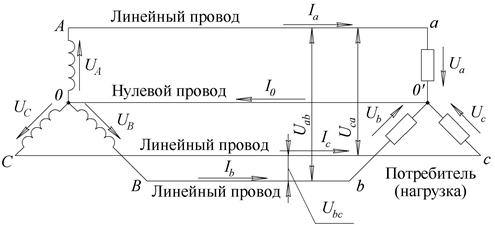
Рис. 1. Трехфазная система, соединение «звездой»
Если нулевой провод отсутствует, схема называется «трехпроводной». На этом же рисунке показаны условные положительные направления линейных напряжений  ,
,  ,
, 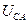 , фазных напряжений источника
, фазных напряжений источника  ,
,  ,
, 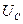 и фазных напряжений на нагрузке
и фазных напряжений на нагрузке 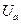 ,
,  ,
,  , а также токов фаз
, а также токов фаз 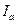 ,
,  ,
, 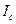 и нулевого провода
и нулевого провода 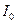 .
.
Если пренебречь падением напряжения в проводящих проводах, то можно считать, что линейные напряжения источника равны соответствующим линейным напряжениям на нагрузке, т.е.
 ,
, 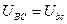 ,
,  .
.
Из приведенной схемы видно, что зависимость между линейными и фазными напряжениями может быть записана согласно II закону Кирхгофа для замкнутого контура:
а) для источника
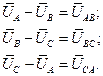
б) для нагрузки (1)

На основании записанных соотношений строится векторная диаграмма напряжений источника, приведенная на рис. 2.
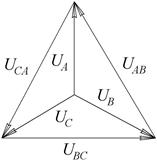
Рис. 2. Векторная диаграмма напряжений источника
По диаграмме видно, что для источника 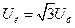 .
.
Из схемы (рис. 1) видно, что ток, протекающий по фазе нагрузки (фазный ток), и ток, протекающий по линейному проводу (линейный ток), одинаковы:
 .
.
Согласно первому закону Кирхгофа для нулевой точки получим зависимость между фазными токами и током нулевого провода:
 (2)
(2)
Значения токов каждой фазы определяется по формуле:
 ,
,  ,
,  . (3)
. (3)
Существует два основных режима работы трехфазной цепи:
а) симметричный, когда все параметры фаз идентичны, а напряжения фаз сдвинуты относительно друг друга на 120˚;
б) несимметричный, когда какое-либо из этих условий не выполняется.
В настоящей работе рассматриваются случаи несимметрии только за счет неодинаковости нагрузок фаз. Система питающих напряжений принимается симметричной.
Уравнения (1) и (2), определяющие зависимости между токами и напряжениями трехфазной цепи, справедливы при любом характере нагрузки как четырехпроводной, так и трехпроводной цепи.
Симметричный режим. Нагрузка всех фаз идентична, т.е. комплексы сопротивлений фаз одинаковы:
 .
.
Следовательно, действующие значения токов фаз
 ,
,  ,
, 
одинаковы, т.е. 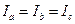 и сдвинуты по фазе относительно соответствующих напряжений на одинаковые углы:
и сдвинуты по фазе относительно соответствующих напряжений на одинаковые углы:
 ,
, 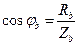 ,
,  , т. е.
, т. е.  .
.
Из векторной диаграммы, приведенной на рис. 3, видно, что ток в нулевом проводе при симметричной нагрузке фаз равен нулю:
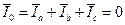 ,
,
следовательно, нулевой провод при равномерной нагрузке фаз необязателен
В данной лабораторной работе фазы нагружаются чисто активными сопротивлениями:
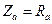 ,
,  ,
,  , т. е.
, т. е.  .
.
и, следовательно, токи совпадают по фазе с соответствующими фазными напряжениями.

Рис. 3. Векторная диаграмма напряжений и токов при симметричной нагрузке
Несимметричный режим.  .
.
Углы сдвига по фазе  ,
, 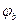 ,
,  между напряжением и током каждой фазы определяются соотношением активной и реактивной составляющих сопротивлений нагрузки фаз. Так как в данной работе нагрузки фаз чисто активные, то эти сдвиги отсутствуют, т.е.
между напряжением и током каждой фазы определяются соотношением активной и реактивной составляющих сопротивлений нагрузки фаз. Так как в данной работе нагрузки фаз чисто активные, то эти сдвиги отсутствуют, т.е.
 .
.
Значения токов каждой фазы определяются по формулам (3).
Рассмотрим два случая: четырехпроводную и трехпроводную схемы.
1. Четырехпроводная схема. В этом случае на каждой фазе нагрузки действует соответствующее фазное напряжение источника, т.е.
 ,
,  ,
,  .
.
В нулевом проводе течет ток
 .
.
Векторная диаграмма такого режима показана на рис. 4.
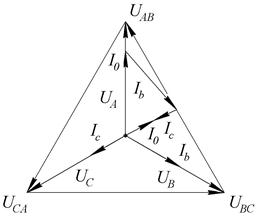
Рис. 4. Векторная диаграмма для схем с нулевым проводом при несимметричной активной нагрузке фаз
2. Трехпроводная схема (обрыв нулевого провода). В этом случае ток нулевого провода отсутствует,  , а между нейтралями источника и потребителя (на обрыве нулевого провода) возникает напряжение
, а между нейтралями источника и потребителя (на обрыве нулевого провода) возникает напряжение  (рис. 5).
(рис. 5).

Рис. 5. Трехпроводная схема трехфазной системы
На векторной диаграмме, показанной на рис. 6, векторы питающих напряжений показаны сплошными линиями. Точка 0 соответствует потенциалу нейтрали источника. Напряжения на нагрузке 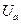 ,
,  ,
,  связаны с линейными напряжениями питания соотношениями (1). Векторы фазных напряжений нагрузки показаны на рис. 6 пунктиром.
связаны с линейными напряжениями питания соотношениями (1). Векторы фазных напряжений нагрузки показаны на рис. 6 пунктиром.
Вектор, соединяющий точки 0 и 0', является вектором напряжения между нейтралями  .
.
Если в процессе эксперимента измерить линейные и фазные напряжения на нагрузке, то точку 0' на топографической векторной диаграмме можно получить методом засечек, сделанных из точек  ,
, 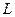 и
и  радиусом, соответствующими действующими значениям напряжений
радиусом, соответствующими действующими значениям напряжений  ,
,  и
и 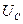 в выбранном масштабе. Согласно уравнению (2) сумма фазных токов для рассматриваемого случая равна нулю (рис. 6, б):
в выбранном масштабе. Согласно уравнению (2) сумма фазных токов для рассматриваемого случая равна нулю (рис. 6, б):
 .
.

Рис. 6. Векторная диаграмма для трехпроводной схемы при несимметричной активной нагрузке фаз: а – напряжений; б – токов
На лабораторной установке нагружение фаз осуществляется включением реостатов. Измерительные приборы включаются по схеме, изображенной на рис. 7. Вольтметр переносной.

Рис. 7. Схема лабораторной установки
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1087; Нарушение авторских прав?; Мы поможем в написании вашей работы!