Использование моделей дискретных сред

Наряду с моделями сплошных сред для описания деформирования массивов горных пород используют модели дискретных сред. В этом случае среду представляют в виде совокупности отдельных частиц, каждая из которых, взятая в отдельности, обладает всеми свойствами твердого тела. Вместе с тем силы сцепления между отдельными частицами отсутствуют вообще, либо настолько малы, что ими можно пренебречь Вследствие этого дискретные среды не воспринимают растягивающих усилий, что резко отличает их от твердых сплошных тел.

В то же время дискретные среды, так же как и твердые тела, способны воспринимать сжимающие нагрузки и по характеру передачи усилий от одной частицы к другой могут быть подразделены на распорные и безраспорные.

В первом случае (рис. 1.3, I) каждая частица ведет себя внутри массива как клин, в силу чего при воздействии внешней вертикальной нагрузки внутри массива возникают горизонтальные составляющие усилия.

Во втором случае распора в среде не возникает, поскольку каждая частица передает нижележащим частицам только вертикальные усилия (рис. 1.3, II).

Важной особенностью дискретных сред и отличием их от сплошных сред является то обстоятельство, что под нагрузкой отдельные её элементы в большей

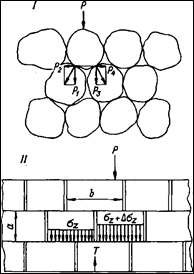
Рис. 1.3. Модели дискретных сред. I — распорная зернистая среда; II — безраспорная среда блочного строения.

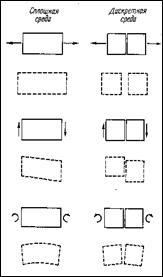
степени смещаются один относительно другого, нежели деформируются. Их относительные смещения можно отнести к трём следующим типам (рис.1.4):

Рис.1.4. Типы смещений элементов дискретной среды.

* расхождение элементов относительно друг друга (в сплошной среде это соответствует развитию деформаций растяжения);

* взаимное скольжение элементов по поверхности контактов (в сплошной среде это соответствует развитию деформаций сдвига);

* взаимный поворот элементов (в сплошной среде это соответствует развитию деформаций изгиба).

Вообще говоря, поскольку дискретные среды состоят из отдельных частиц-зерен, к ним лишь условно можно применять понятие «напряжения». При этом под «напряжениями» в механике дискретных сред понимают усилия на отдельные частицы, отнесенные к площади сечения этих частиц. Таким образом напряжение в какой-либо точке дискретной среды есть величина случайная, и для того, чтобы характеризовать напряженное состояние какого-либо бесконечно малого объема, необходимо усреднять значения напряжений в отдельных зернах. Подобное усреднение может быть представлено и как оперирование с некоторым объемом эквивалентной сплошной среды, напряженное состояние которого в среднем соответствует напряженному состоянию равновеликого объема дискретной среды

Применение к дискретной среде понятия «деформация» также имеет некоторую условность. Под влиянием приложенных усилий отдельные частицы могут деформироваться сами, перемещаться поступательно и с поворотом, в результате чего происходит переупаковка частиц и может изменяться плотность среды. В соответствии с этим под деформациями какого-либо объема дискретной среды также понимают деформации равновеликого объема сплошной упругой среды, т. е. и в этом случае производят замену дискретной среды некоторой эквивалентной ей сплошной средой.

Для дискретных сред справедливы уравнения равновесия в форме равенств для условий сплошной среды. Однако необходимо помнить, что они выполняются лишь статистически, т. е. в среднем для какой-либо области.

Вместе с тем в отличие от сплошных сред к дискретным средам не могут быть применены уравнения совместности деформаций. Вместо них для дискретных сред существуют свои соотношения между компонентами напряжений и деформаций.

В частности, в дискретных средах любые две частицы (блока) связываются друг с другом через третью. При этом в случае, если вертикальные усилия на них будут различными, то в связывающем их блоке возникает перерезывающая сила Т (рис. 1.3, II), которая в первом приближении может быть принята пропорциональной разности вертикальных усилий. В свою очередь, от перерезывающей силы легко перейти к касательным напряжениям, действующим в связывающем блоке (частице), и, таким образом, получить соотношения между касательными и нормальными компонентами напряжений в дискретной среде. Эти соотношения характеризуют способность рассматриваемых сред распределять действующие нагрузки.

Уравнения, характеризующие распределительную способность дискретной среды, называют физическими уравнениями. Однако в отличие от физических уравнений для сплошных сред, отражающих взаимосвязи между компонентами напряжений и деформаций, они имеют форму соотношений компонент напряжений, действующих в массиве.

Cоотношениям между компонентами напряжений в дискретных средах соответствуют и определенные соотношения между компонентами деформаций, которые по сути аналогичны уравнениям неразрывности для сплошной среды.

Итак, для описания напряженно-деформированного состояния дискретных сред в настоящее время разработаны некоторые общие подходы, а также имеются решения для некоторых частных случаев. Однако существенную трудность представляют экспериментальные определения параметров, характеризующих структурные особенности дискретных сред.

В классе моделей дискретных сред выделяются модели блочных сред. Они занимают промежуточное положение между моделями сплошной среды и моделями идеально дискретной среды. От моделей сплошной среды они отличаются тем, что среда сложена различными блоками (не обязательно правильной формы) с реальными размерами, а от моделей дискретной среды - тем, что здесь уже нельзя пренебрегать силами взаимодействия между блоками. Именно такие подходы в наибольшей степени отражают реальное поведение массивов горных пород. В последнее время, благодаря прогрессу в вычислительной технике, достигнуты существенные успехи в методах решения подобных задач.

В заключение необходимо остановиться ещё на одном вопросе, касающемся понятий и терминов геомеханики.

До недавнего времени центральным понятием в геомеханике являлось понятие «горное давление». Именно с ним связывались основные процессы геомеханики. Вопрос отыскания и формулирования определения, наиболее точно и строго отражающего это понятие был неоднократно предметом обсуждений и публичных дискуссий на различных кворумах и в научно-технической литературе. Большинство специалистов, предлагая различные формулировки, так или иначе связывало его с понятием силы, имея в виду объёмные силы (в частности, силы тяжести), объективно существующие в массиве пород.

В настоящее время этот термин утратил своё значение, употребляется лишь как образное выражение с широким качественным смыслом первопричины всех механических явлений в массиве пород.

Современным термином является термин «напряженно-деформированное состояние массива пород», исчерпывающе отражающее состояние массива как при наличии выработок, так и при их отсутствии. В последнем случае говорят о начальном или естественном напряженно-деформированном состоянии ненарушенного массива пород, т.е. до проведения горных работ.

Вместе с тем следствием отживающего термина «горное давление» является до сих пор широко используемое понятие «проявления горного давления», под которым понимают деформации, сдвижения и разрушения горных пород, а также результаты силового взаимодействия между породами и крепью, другими словами, результаты действия процессов геомеханики.

Также достаточно широко используется понятие применительно к тем или иным классам систем разработки месторождений полезных ископаемых. Весьма часто термин «управление горным давлением» равнозначен термину «управление кровлей», особенно это характерно для систем разработки пластовых месторождений. В последнее время всё чаще вместо термина «управление горным давлением» употребляют более общее понятие «управление состоянием массива горных пород», понимая при этом проведение некоторого комплекса мероприятий, направленного на поддержание в работоспособном и безопасном состоянии выработок и призабойных зон, где непосредственно располагаются люди и механизмы для добычи полезного ископаемого.

Дата добавления: 2014-11-29