КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задач
|
|
|
|
Задача 1. Вычислить:
а) 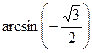 ; б)
; б)  ; в)
; в) 
Решение:
а) 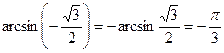 , т.к.
, т.к. 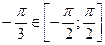 и
и 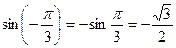 ;
;
б) 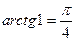 , т.к.
, т.к. 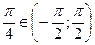 и
и 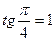 ;
;
в) 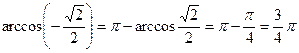 , т.к.
, т.к. 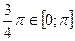 и
и 
 .
.
Задача 2. Решить уравнения:
а)  ; б)
; б) 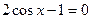 ; в)
; в)  ; г)
; г) 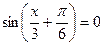
Решение:
а)  . Решение найдём по формуле
. Решение найдём по формуле 
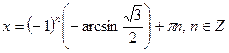


б) 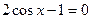 ;
;
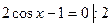
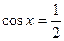 . Решение найдём по формуле
. Решение найдём по формуле 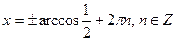 .
.

в)  . Введём новую переменную
. Введём новую переменную  , тогда
, тогда 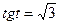 . Решение находим по формуле:
. Решение находим по формуле: 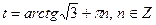 .
.
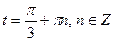 или
или  ;
;
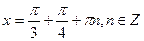 ,
,
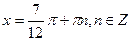 .
.
г) 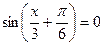 . Введём новую переменную
. Введём новую переменную 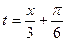 , тогда
, тогда 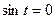 . Используя частные случаи решения, получим:
. Используя частные случаи решения, получим: 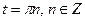 , или
, или 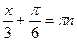 .
.
Тогда  ,
,
 .
.
Задача 3. Решить неравенства:
а) 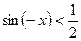 ; б)
; б)  ; в)
; в) 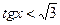 .
.
Решение:
а)
| Неравенство 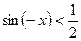 равносильно неравенству равносильно неравенству  , или , или 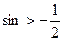 на единичной окружности отметим точки, синус которых равен на единичной окружности отметим точки, синус которых равен  (это можно сделать, проведя прямую (это можно сделать, проведя прямую 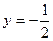 или используя таблицу значений тригонометрических функций). Отмеченным точкам соответствуют числа или используя таблицу значений тригонометрических функций). Отмеченным точкам соответствуют числа 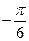 и и  соответственно. Т.к. неравенство строгое, то отмеченные точки выделим соответственно. Т.к. неравенство строгое, то отмеченные точки выделим
|
«пустыми» кружками. Затем отметим точки, для которых 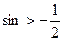 . Чтобы записать решение, будем двигаться против часовой стрелки от одной из главных точек к другой, так, чтобы «пройти» по всем точкам решения. Получим
. Чтобы записать решение, будем двигаться против часовой стрелки от одной из главных точек к другой, так, чтобы «пройти» по всем точкам решения. Получим  . Чтобы получить все решения неравенства, добавим к границам неравенства период функции
. Чтобы получить все решения неравенства, добавим к границам неравенства период функции 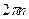 , тогда
, тогда  где
где 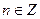 .
.
б)
| Отметим на единичной окружности точки, для которых 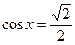 закрашенными кружками (это можно сделать, проведя прямую закрашенными кружками (это можно сделать, проведя прямую 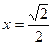 или, используя таблицу значений тригонометрических функций). Главным точкам соответствуют числа или, используя таблицу значений тригонометрических функций). Главным точкам соответствуют числа 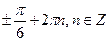 . Затем отметим точки, для которых . Затем отметим точки, для которых 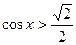 . Запишем решение «двигаясь» от одной . Запишем решение «двигаясь» от одной
|
главной точки к другой против часовой стрелки, так, чтобы пройти все точки решения и получим
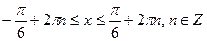 или
или
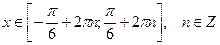 .
.
в)
| Отметим на единичной окружности «пустым» кружком точки, для которых 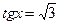 и и 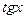 не существует. Из 4 – х образовавшихся промежутков выделим те, на которых не существует. Из 4 – х образовавшихся промежутков выделим те, на которых 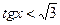 . Заметим, что решение неравенства на одном из промежутков получаются из решений на другом из промежутков добавляем . Заметим, что решение неравенства на одном из промежутков получаются из решений на другом из промежутков добавляем 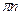 . Двигаясь против часовой стрелки от одной из главных точек к другой, получим ответ . Двигаясь против часовой стрелки от одной из главных точек к другой, получим ответ  или или
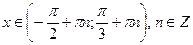 . .
|
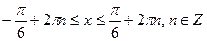 или
или
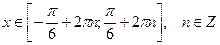 .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 294; Нарушение авторских прав?; Мы поможем в написании вашей работы!