Средняя и сигма суммарной группы

Проверка выпадов (артефактов)

Нормированное отклонение помогает определить выпады, или артефакты, т. е. такие записанные значения признака, которые резко отличаются от всех других значений признака в группе. Проверка артефактов должна проводиться всегда перед началом обработки полученных первичных данных. Если подтвердится, что резко выделяющееся значение действительно не может относиться к объектам данной группы, и попало в записи вследствие ошибок внимания, следует такой артефакт исключить из обработки.

Проверка артефактов может производиться по критерию, равному нормированному отклонению выпада:

, (7.9)

где:

Т – критерий выпада;

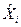– выделяющееся значение признака (или очень большое или очень малое);

μ, s – средняя и сигма, рассчитанные для группы, включающей артефакт;

T_st – стандартные значения критерия выпадов, определяемых по таблице 7.3.

Таблица 7.3 – Стандартные значения критерия выпадов (T_st)

n	Tst	n	Tst	n	Tst	n	Tst
	2,0	16 – 20	2,4	47 – 66	2,8	125 – 174	3,2
3 – 4	2,1	21 – 28	2,5	67 – 84	2,9	175 – 349	3,3
5 – 9	2,2	29 – 34	2,6	85 – 104	3,0	350 – 599	3,4
10 – 15	2,3	35 – 46	2,7	105 – 124	3,1	600 – 1500	3,5

Если Т ≥ T_st, то анализируемое значение признака является артефактом. Альтернатива Т < T_st не позволяет исключить из анализа значение признака.

Табулированные данные таблицы 7.3 можно аппроксимировать следующей функцией: T_st = 0,287×ln(n) + 1,714

Пример

Данные: 1, 2, 3, 10; n = 4, μ = 4, s = 4, 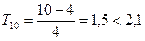; 10 еще не может считаться выпадом.

Данные: 1, 2, 2, 3, 3, 4, 4, 5, 21; n = 9, μ = 5, s = 6,1, ;

21 может считаться выпадом и должна быть исключена из обработки.

Иногда бывает необходимо определить среднюю и сигму для суммарного распределения, составленного из нескольких распределений. При этом известны не сами распределения, а только их средние и сигмы.

Средняя и сигма в таких случаях находятся по следующим формулам:

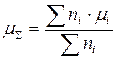(7.10)

, (7.11)

где:

n_i – численность отдельных объединяемых групп;

μ_i – средняя арифметическая каждой объединяемой группы;

s_i – сигма каждой объединяемой группы.

Пример

Четыре независимых наблюдения величины одного и того же вида амеб в сходных условиях дали следующие результаты (в микронах):

Наблюдения	μ	s	n

По этим данным средний размер и стандартное отклонение амеб могут быть вычислены, как показано в таблице 7.4.

Разнообразие объектов, составляющих группу, – основное свойство всякой совокупности. Знание закономерностей, по которым формируется разнообразие признака в группе, имеет большое практическое и научное значение.

В малочисленных группах трудно подметить какую–либо закономерность в разнообразии данных. Обычно все значения бывают различны, повторяются без всякой видимой закономерности.

Таблица 7.4 – Вычисление μ и σ суммарной группы

Исследования
ni
μ i					–
si					–
ni μi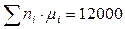
si^2
(ni-1) si^2
	–1	+ 1		+1

; ; .

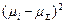
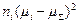
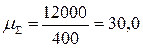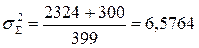Дата добавления: 2014-11-29