Метод множників Лагранжа

Якщо

У разі, якщо

,

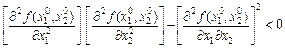то в точці (x ₁⁰, x ₂⁰) функція f (x ₁, x ₂) екстремуму не має.

,

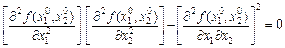то питання про існування екстремуму залишається відкритим.

Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції. Термін «умовний» означає, що змінні задачі мають задовольняти деякі умови.

Розглянемо таку задачу для випадку двох змінних:

знайти max(min) f (x ₁, x ₂) (8.4)

за умови, що q (x ₁, x ₂)= b. (8.5)

Найпростіший спосіб розв’язання задачі такого виду полягає в тому, що спочатку з обмеження (8.5) знаходять вираз однієї змінної через іншу. Приміром, визначають x ₂ через x ₁. Отриманий вираз виду x ₂= g (x ₁) підставляють у функцію (8.4), що після цього стає функцією однієї змінної f (x ₁, g (x ₁)), і далі знаходять її безумовний екстремум.

Якщо деяка точка x ₁^* є точкою екстремуму функції f (x ₁, g (x ₁)), то точка X ^*(x ₁^*, x ₂^*= g (x ₁^*)) є точкою умовного екстремуму функції (8.4) за умови (8.5).

Однак не завжди вдається відшукати аналітичний вираз однієї змінної через іншу в умові (8.5). Часто це досить важко здійснити або неможливо. Також іноді складно узагальнити даний спосіб для функції n змінних, на які накладено m обмежень. Тому описана досить проста ідея зведення задачі відшукання умовного екстремуму функції кількох змінних до задачі на безумовний екстремум функції однієї змінної не може бути використана як основа універсального методу розв’язування задач на умовний екстремум. Цікавий метод розв’язування задач типу (8.4), (8.5) запропонував Лагранж.

Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення подальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.

У попередньому параграфі наведена необхідна умова існування локального екстремуму неперервної та диференційовної функ­ції двох змінних.

Узагальнення необхідної умови існування локального екстремуму функції n змінних має аналогічний вигляд. Отже, для роз­в’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції.

Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:

max(min) Z = f (x ₁, x ₂,…, x_n) (8.6)

за умов:

q_i (x ₁, x ₂,…, x_n)= b_i i =1,… m, (8.7)

де функції f (x ₁, x ₂,…, x_n) і q_i (x ₁, x ₂,…, x_n) мають бути диференційовними.

Задача (8.6), (8.7) полягає в знаходженні екстремуму функції f (x) за умов виконання обмежень q_i, i =1,… m.

Переходимо до задачі пошуку безумовного екстремуму. В літературі [13, 28] теоретично доведено, що постановки та розв’я­зання таких задач еквівалентні.

Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:

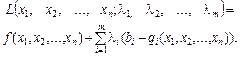(8.8)

де λ _i — деякі невідомі величини, що називаються множниками Лагранжа.

Знайдемо частинні похідні і прирівняємо їх до нуля:

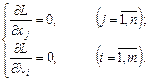
(8.9)

Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування.

Система (8.9), як правило, нелінійна.

Розв’язками її є X ^*= x ₁^*, x ₂^*, …x_n ^* і λ=λ₁^*,λ₂^*, … λ _m ^* — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6), (8.7) або можуть бути точками перегину (сідловими точками).

Для діагностування стаціонарних точок і визначення типу екстремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій Z = f (x ₁, x ₂,…, x_n), q_i (x ₁, x ₂,…, x_n) існують другі частинні похідні і вони неперервні).

Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функ­цією Лагранжа виду (8.8) будується матриця Гессе, що має блочну структуру розмірністю (m+n)× (m+n):

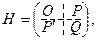
де О — матриця розмірністю (m × m), що складається з нульових елементів,

Р — матриця розмірністю (m × n), елементи якої визначаються так:

,

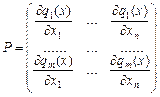P' — транспонована матриця до Р розмірністю (n × m),

Q — матриця розмірністю (n × n) виду:

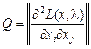, де .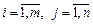

Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати X ^*= x ₁^*, x ₂^*, …x_n ^* і λ=λ₁^*,λ₂^*, … λ _m ^*.

1. Точка X ^* є точкою максимуму, якщо, починаючи з голов­ного мінору порядку (m + 1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником (-1) ^{m +1}.

2. Точка X ^* є точкою мінімуму, якщо, починаючи з головного мінору порядку (m + 1), знак наступних (n – m) головних мінорів матриці Н визначається множником (-1) ^m.

Розглянемо задачу, розв’язок якої знайдемо методом множників Лагранжа.

Акціонерне товариство з обмеженою відповідальністю виділило 1200 га ріллі під основні сільськогосподарські культури — озиму пшеницю і цукрові буряки.

У табл. 8.1 маємо техніко-економічні показники вирощування цих культур:

Таблиця 8.1

Показник	Озима пшениця х 1, сотні га	Цукрові буряки х 2, сотні га
Урожайність, т/га
Ціна, грн/т
Собівартість, грн/т	y 1 = 12,5 х 1^2 - 200 х 1 + 1200	y 1 = 12,5 х 2^2 - 150 х 2 + 650

Необхідно знайти оптимальні площі посіву озимої пшениці та цукрових буряків.

Нехай: х ₁ — площа ріллі під озимою пшеницею, сотні га;

х ₂ — площа ріллі під цукровими буряками, сотні га.

Звернемо увагу на те, що собівартість тонни пшениці та цукрових буряків залежить від відповідної площі посіву.

Запишемо економіко-математичну модель цієї задачі. Критерієм оптимальності візьмемо максимізацію чистого доходу:

max f =4(800-12,5 х ₁² + 200 х ₁ - 1200) х ₁100+

35(300-12,5 х ₂² + 150 х ₂ - 650) х ₂100=

400(-12,5 х ₁³ + 200 х ₁² - 400 х ₁)+3500(-12,5 х ₂³ + 150 х ₂² - 350 х ₂)

за умов:

х ₁+ х ₂=12

Запишемо функцію Лагранжа:

L (х ₁, х ₂,λ₁)= 400(-12,5 х ₁³ + 200 х ₁² - 400 х ₁)+3500(-12,5 х ₂³ + 150 х ₂² - 350 х ₂)+ λ₁(12- х ₁- х ₂).

Візьмемо частинні похідні і прирівняємо їх до нуля:

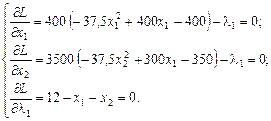
З цієї системи рівнянь визначаємо координати сідлових точок. З першого та другого рівняння знаходимо l₁ і, прирівню­ючи вирази, маємо:

400(-37,5 х ₁² + 400 х ₁ - 400)=3500(-37,5 х ₂² + 300 х ₂ - 350) (8.10)

або, скоротивши на 100 обидві частини і розкривши дужки, отримаємо:

150 х ₁² - 1600 х ₁ + 1600=1312,5 х ₂² - 10500 х ₂ + 12250. (8.11)

Із останнього рівняння системи маємо: х ₁=12- х ₂.

Підставимо вираз для х ₁ у рівність (8.11). Отримаємо:

150(12- х ₂)² - 1600(12- х ₂) + 1600=1312,5 х ₂² - 10500 х ₂ + 12250

або

150(144-24 х ₂+ х ₂²)-19200+1600 х ₂+1600=1312,5 х ₂² - 10500 х ₂ + 12250,

21600+3600 х ₂-150 х ₂²[phone] х ₂+1600+

+1312,5 х ₂² - 10500 х ₂ + 12250=0.

Отже, 1162 х ₂²-8500х₂+11450=0;

D=72250000-53219600=19030400

.

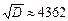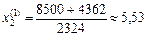(553 га);

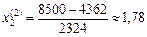(178 га).

Відповідно дістаємо:

х ₁⁽¹⁾≈6,47(647 га);

х ₁⁽²⁾≈10б22(1022 га).

Тобто отримали дві сідлові точки:

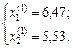
Перевіримо за допомогою достатньої умови існування екстремуму спочатку екстремальну точку X ₁^*(х ₁⁽¹⁾, х ₂⁽¹⁾).

Матриця Гессе має такий вигляд:

.

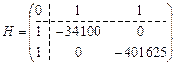За вищезазначеним правилом визначаємо головні мінори, починаючи з 2-го порядку (m +1=1+1=2):

,

.

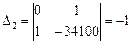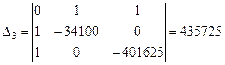Отже, головні мінори утворюють знакозмінний ряд та, починаючи з головного мінору 2-го порядку, наступний мінор визначається знаком (-1) ^{m +1}=(-1)², тобто X ₁^*(х ₁⁽¹⁾, х ₂⁽¹⁾) є точкою максимуму.

Обчислимо значення цільової функції в цій точці:

f (х ₁⁽¹⁾=6,47; х ₂⁽¹⁾=5,53)=4(800-532,26+1294-1200)647+

+35(300-382,26+829,5-650)553=4625863

Аналогічні обчислення для точки X ₁^*(х ₁⁽²⁾=10,22; х ₂⁽²⁾=1,78) показують, що вона не є екстремальною.

Отже, цільова функція набуде максимального значення, якщо озима пшениця вирощуватиметься на площі 647 га, а цукрові буряки — на площі 553 га.

Метод множників Лагранжа може застосовуватися також у разі наявності обмежень на знаки змінних і обмежень-нерів­ностей.

Розглянемо таку задачу в загальному вигляді:

max(min) F=f (x ₁, x ₂,…, x_n),

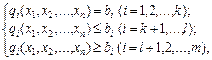
причому всі функції, що входять у задачу, мають бути диференційовними хоча б один раз.

Очевидно, що введення в ліві частини нерівностей системи обмежень задачі додаткових невід’ємних змінних x_n+i ≥0 (i = k +1, …, m) перетворює початкову задачу в таку, що містить лише обмеження-рівності, тобто яка за формою та методом розв'язування збігатиметься з задачею (8.6), (8.7). Особливості розв'язання такого типу задач розглянуто в літературі: [19], [28].

8.5. Необхідні умови існування сідлової точки

Для розроблення методів розв’язування окремих типів задач нелінійного програмування важливе значення має поняття сідлової точки, а також визначення необхідних і достатніх умов існування сідлових точок функції Лагранжа L (X, Λ) у (n + m)-вимірному просторі змінних (x ₁, x ₂, …x_n,λ₁,λ₂, … λ _m) за довільних умов, які можуть накладатися на їх знаки (необхідні і достатні умови існування сідлової точки функції Лагранжа за відсутності обмежень на знаки змінних розглянуто в § 8.4).

Розглянемо нелінійну задачу:

max F=f (x ₁, x ₂,…, x_n),

.

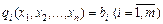Причому на компоненти векторів X, Λ накладено обмеження на знаки. Позначимо множину точок, що задовольняють такі обмеження, через Ω.

Функція Лагранжа для цієї задачі має вигляд:

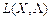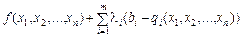= . (8.12)

Точка (X, ^* Λ ^*)=(x ₁^*, x ₂^*, …x_n ^*,λ₁^*,λ₂^*, … λ _m ^*) називається сідловою точкою функції Лагранжа (8.12), якщо для всіх 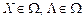виконується співвідношення:

L (X, Λ^*)≤ L (X^*, Λ^*)≤ L (X^*, Λ). (8.13)

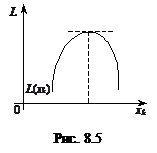Для диференційовних функцій f (X) та q_i (X) знайдемо необхідні умови існування сідлової точки.

Сідлова точка (X, ^* Λ ^*)=(x ₁^*, x ₂^*, …x_n ^*,λ₁^*, λ₂^*, … λ _m ^*) функції L (X, Λ) виду (8.12) за означенням задовольняє умову:

L (X, Λ^*)≤ L (X^*, Λ^*).

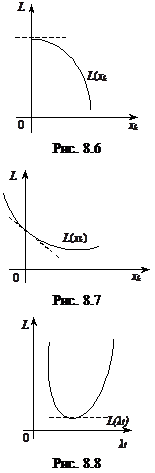Нерівність виконується для всіх точок Х, тобто також і для тих, у яких лише одна координата відрізняється від Х ^*. Допустимо, що це х_k, а всі інші збігаються з координатами сідлової точки x_j=x_j^* (j =1,2,…, k- 1, k +1,…, n).

Оскільки права частина нерівності є фіксованою, а в лівій частині змінюється лише одна координата х_k, то приходимо до функ­ції однієї змінної L (X, Λ^*)= L (x_k), яку можна зобразити графічно на координатній площині.

Розглянемо спочатку випадок, коли х_k ≥0, тобто лише частину координатної площини, для якої х_k ≥0.

Можливі такі випадки:

1) коли всі x_j^* >0, то максимальне зна­чення функції L (x_k) досягатиметься в точці, для якої ∂ L (X^*, Λ^*)/∂ х_k =0 (рис. 8.5).

2) коли максимум функції L (x_k) досягатиметься в точці х_k =0 і розглядувана частинна похідна також дорівнюватиме нулю: ∂ L (X^*, Λ^*)/∂ х_k =0 (рис. 8.6).

3) коли точка максимуму функції L (x_k) досягатиметься також у точці х_k =0, а частинна похідна ∂ L (X^*, Λ^*)/∂ х_k ≤0 (рис. 8.7).

Узагальнюючи всі три ситуації, маємо:

∂ L (X^*, Λ^*)/∂ х_j ≤0 для х_j ≥0

та .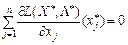

Розглядаючи другу частину нерівності (8.13):

L (X^*, Λ^*)≤ L (X^*, Λ)

аналогічними міркуваннями, що проілюстровані рис. 8.8.—8.10, встановлюються необхідні умови для похідних по функції Лагранжа в сідловій точці.

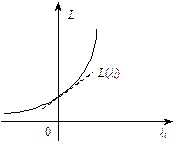
Рис. 8.9 Рис. 8.10

Об’єднуючи всі три випадки для невід’ємних координат, маємо необхідні умови сідлової точки:

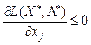для тих індексів j, де 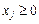. (8.14)

Зауважимо, що для 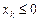маємо ті самі випадки, які зображено на рис. 8.1—8.6, причому графіки будуть симетрично відоб­ражені відносно осі Оy, тобто для недодатних координат необхідна умова має вигляд:

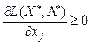для тих індексів j, де 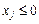. (8.15)

І нарешті, як відомо з попереднього параграфа, якщо на знак х_j умови не накладаються, то необхідною умовою є:

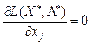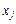, — довільного знака. (8.16)

Узагальнення всіх випадків приводить до рівняння:

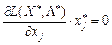. (8.17)

Розглядаючи другу частину нерівності (8.13), за допомогою аналогічних міркувань встановлюємо необхідні умови для похідних по 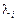функції Лагранжа в сідловій точці:

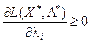для тих індексів і, де 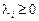, (8.18)

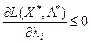для тих індексів і, де , (8.19)

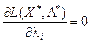для тих індексів і, де 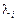має довільний знак. (8.20)

Отже, справджується рівняння:

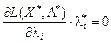. (8.21)

Сукупність співвідношень (8.14)—(8.21) становить необхідні умови, які має задовольняти сідлова точка X^*, Λ^* функції Лагранжа для точок, що належать множині Ω. При цьому L (X^*, Λ^*) повинна мати частинні похідні по всіх компонентах векторів X, Λ.

8.6. Теорема Куна—Таккера

Розглянутий метод множників Лагранжа уможливлює знаходження лише локальних сідлових точок функції Лагранжа.

Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки.

Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:

max F = f (X), (8.22)

, (8.23)

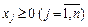. (8.24)

(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)).

Теорема 8.1. (Теорема Куна—Таккера). Вектор Х^* є оптимальним розв’язком задачі (8.22)—(8.24) тоді і тільки тоді, коли існує такий вектор Λ^*, що при X^*≥ 0, Λ^*≥ 0 для всіх X≥ 0, Λ≥ 0 точка (X^*, Λ^*) є сідловою точкою функції Лагранжа

,

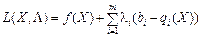і функція мети f (X) для всіх 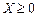угнута, а функції 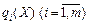— опуклі.

Доведення. Необхідність. Нехай Х^* — оптимальний план задачі (8.22)—(8.24), тобто є точкою глобального максимуму задачі. Отже, для всіх інших планів задачі Х з множини допустимих розв’язків виконуватиметься співвідношення:

f (X^*)≥ f (X).

Розглянемо тепер вектор 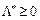, що відповідає точці глобального максимуму 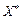, і значення функції Лагранжа в точках 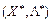, , 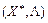, 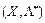де 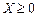— довільний план задачі з множини допустимих розв’язків, 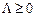— вектор множників Лагранжа, що відповідає Х.

З умови (8.21) маємо: 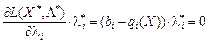, тоді

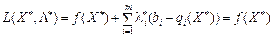. (8.25)

Для точки з координатами 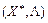деякі доданки виду 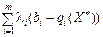можуть бути відмінними від нуля. Оскільки за умовою задачі 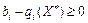, то лише за умови, що 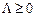, матимемо нерівність:

.

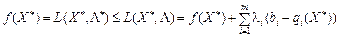Функція 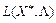— лінійна відносно 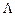, тобто остання нерівність виконується для будь-якого 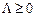. Отже, точка 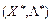— точка глобального мінімуму по 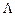функції Лагранжа.

Для встановлення нерівності, що відповідає лівій частині умови (8.13), а саме: 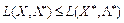, скористаємося також рівнянням (8.21), підсумувавши його по і: 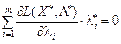. За умовою теореми f (X), q_i (X) — угнуті функції і 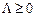, тому виконується таке рівняння:

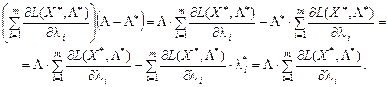
Отже, у точці Х ^* функція Лагранжа має глобальний максимум по Х, що повністю доводить необхідність теореми.

Достатність. Для доведення достатності умов теореми потрібно виходити з того, що 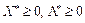, 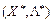— сідлова точка функції 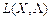(тобто для 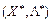виконується нерівність (8.13)), і необхідно довести, що тоді Х ^* є оптимальним планом задачі опуклого програмування.

Підставимо у нерівність (8.13) вираз функції Лагранжа (8.12) для задачі (8.22)—(8.23):

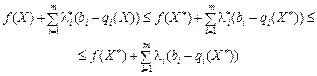(8.26)

при всіх значеннях .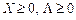

Розглянемо праву частину подвійної нерівності (8.26).

.

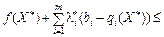
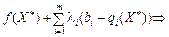
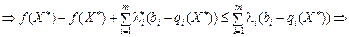
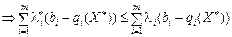Остання нерівність має виконуватися для всіх 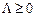. Крім того, 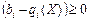, тобто нерівність справджується лише у разі, коли

.

Тоді з лівої частини нерівності (8.26) маємо:

.

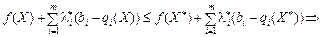
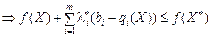Через те що 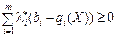, приходимо до нерівності f (X)≤ f (X^*), яка справджується для всіх значень .

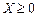Отже, точка Х ^* задовольняє обмеження і надає максимального значення цільовій функції задачі, тому що для всіх інших 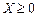функція f (X) набуває менших значень, ніж у точці Х ^*, тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов тереми доведено.

Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції.

8.6.1. Опуклі й угнуті функції

Наведемо основні означення та теореми. Нехай задано n -вимірний лінійний простір Rⁿ. Функція f (X), що задана на опуклій множині 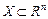, називається опуклою, якщо для будь-яких двох точок 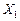та 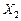з множини X і будь-яких значень 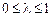виконується співвідношення:

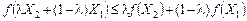. (8.27)

Якщо нерівність строга і виконується для 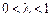, то функція f (X) називається строго опуклою.

Функція f (X), яка задана на опуклій множині 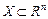, називається угнутою, якщо для будь-яких двох точок 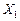та 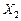з множини X і будь-якого 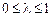справджується співвідношення:

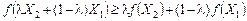. (8.28)

Якщо нерівність строга і виконується для 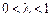, то функція f (X) називається строго угнутою.

Слід зазначити, що опуклість та угнутість функції визначаються лише відносно опуклих множин у 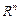, оскільки за наведеними означеннями разом з двома будь-якими точками 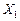та 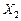множині X належать також точки їх лінійної комбінації: 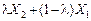для всіх значень 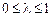, що можливо лише у разі, коли множина X є опуклою.

Теорема 8.2. Нехай f (X) — опукла функція, що задана на замкненій опуклій множині X, тоді будь-який локальний мінімум f (X) на цій множині є і глобальним.

Доведення. Допустимо, що в точці 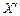функція f (X) має локальний мінімум, тоді як глобальний мінімум досягається в точці 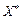, отже, виконуватиметься нерівність f (X')> f (X^*). Через те що f (X) — опукла функція, для будь-яких значень 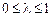справджується співвідношення:

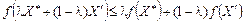. (8.29)

Множина Х опукла, тому точка 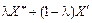при 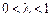також належить цій множині. Враховуючи, що f (X')> f (X^*), нерів­ність (8.29) матиме вигляд:

;

.

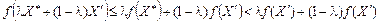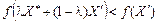Значення 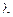можна вибрати так, щоб точка 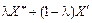була розташована як завгодно близько до 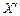. Тоді отримана остання нерівність суперечить тому, що 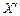— точка локального мінімуму, оскільки існує як завгодно близька до неї точка, в якій функція набуває меншого значення, ніж у точці 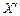. Тому попереднє допущення неправильне. Теорему доведено.

Теорема 8.3. Нехай f (X) — опукла функція, що визначена на опуклій множині Х, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках Х. Нехай 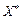— точка, в якій 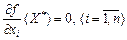. Тоді в точці 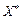досягається локальний мінімум, що збігається з глобальним.

Доведення. З рівності (8.12) для 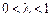знаходимо:

;

;

.

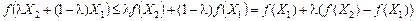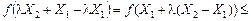
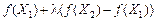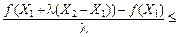
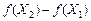Через те що існують частинні похідні першого порядку, функцію 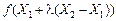можна розкласти в ряд Тейлора:

,

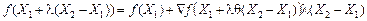де 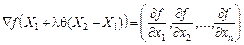— градієнт функції f, обчислений у точці 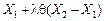, 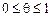. Тоді:

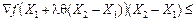
≤f (X ₂)- f (X ₁).

Переходимо до границі при 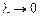, отримаємо:

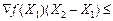
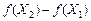. (8.30)

Ця умова виконується для будь-яких внутрішніх точок Х ₁ та Х ₂ і є необхідною і достатньою умовою опуклості f (X).

Якщо функція f (X) неперервна разом з частинними похідними першого порядку і угнута на множині Х, то аналогічно поперед­ньому результату маємо:

.

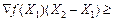
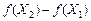Припустимо, що Х ⁰ — довільна точка множини Х, тоді, взявши 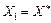, , 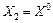а також за умовою теореми 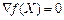, в нерівності (8.30) маємо:

.

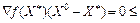
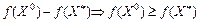Отже, опукла функція f (X) досягає свого глобального мінімуму на множині Х у кожній точці, де 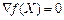. Теорему доведено.

Як наслідок теореми можна показати, що коли Х замкнена, обмежена знизу, опукла множина, то глобального максимуму опукла функція f (X) досягає на ній у одній чи кількох точках (при цьому допускається, що в точці Х значення функції скінченне). Застосовуючи за розв’язування таких задач процедуру перебору крайніх точок, можна отримати точку локального максимуму, однак не можна встановити, чи є вона точкою глобального максимуму.

Для угнутих функцій отримані результати формулюють так. Нехай f (X) — угнута функція, що задана на замкненій опуклій множині X Ì Rⁿ. Тоді будь-який локальний максимум f (X) на множині Х є глобальним. Якщо глобальний максимум досягається в двох різних точках множини, то він досягається і на нескінченній множині точок, що лежать на відрізку, який сполучає ці точки. Для строго угнутої функції існує єдина точка, в якій вона досягає глобального максимуму.

Градієнт угнутої функції f (X) у точках максимуму дорівнює нулю, якщо f (X) — диференційовна функція. Глобальний мінімум угнутої функції, якщо він скінченний на замкненій обмеженій зверху множині, має досягатися в одній чи кількох її крайніх точках за умови скінченності функції f (X) у кожній точці цієї множини.

8.7. Опукле програмування

Опукле програмування розглядає методи розв’язування задач нелінійного програмування, математичні моделі яких містять опуклі або угнуті функції.

Загальний вигляд задачі опуклого програмування такий:

max F=f (x ₁, x ₂,…, x_n), (8.31)

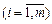, ; (8.32)

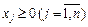, (8.33)

де F=f (x ₁, x ₂,…, x_n), 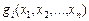— угнуті функції.

Аналогічний вигляд має задача для опуклих функцій.

Позначимо: 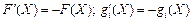, тоді 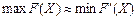, і маємо:

min F' = f ' (x ₁, x ₂,… x_n), (8.34)

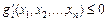
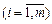; (8.35)

, (8.36)

де F'=f ' (x ₁, x ₂,…, x_n),, 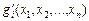— опуклі функції.

Оскільки ці задачі еквівалентні, то нижче розглянемо задачу (8.31)—(8.33).

Множина допустимих планів задачі, що визначається системою (8.32), є опуклою.

Як наслідок теорем 8.2 та 8.3 справджується таке твердження: точка локального максимуму (мінімуму) задачі опуклого програмування (8.31)—(8.33) є одночасно її глобальним максимумом (мінімумом).

Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму).

У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа.

Функція Лагранжа для задачі (8.31)—(8.33) має вид:

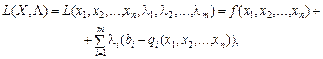(8.37)

де 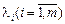— множники Лагранжа.

Використовуючи теорему Куна — Таккера, маємо необхідні та достатні умови існування оптимального плану задачі опуклого програмування.

Теорема 8.4. Якщо задано задачу нелінійного програмування виду (8.31)—(8.33), де функції f (X), g_i (X) 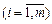диференційовні і вгнуті по Х, то для того, щоб вектор 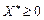був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор 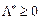, що пара (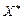, 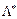) була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови:

(І) 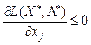, 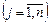; (8.38)

(ІІ) 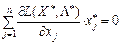, 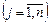; (8.39)

(ІІІ) 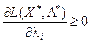, 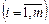; (8.40)

(IV) 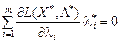, 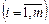. (8.41)

Для задачі мінімізації (8.34)—(8.36), де всі функції f (X), g_i (X) (i =1,… m) диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (8.39) та (8.41).

Сформульована теорема доводиться з допомогою використання вищенаведених теорем цього та попередніх параграфів.

8.8. Квадратичне програмування

Окремою частиною задач опуклого програмування є задачі квадратичного програмування. До них належать задачі, які мають лінійні обмеження, а функціонал являє собою суму лінійної і квадратичної функцій:

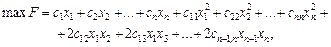
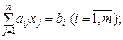
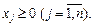
Дата добавления: 2014-11-29